Геометрическая вероятность
Пример 1.
Доказать, что 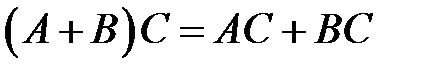 .
.
Решение.
Пусть 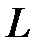 – исход опыта, благоприятствующий наступлению
– исход опыта, благоприятствующий наступлению 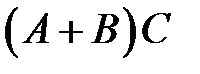 , следовательно
, следовательно 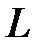 благоприятен наступлению и
благоприятен наступлению и 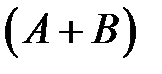 и
и  , следовательно
, следовательно 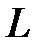 благоприятствует наступлению хотя бы одного события и
благоприятствует наступлению хотя бы одного события и 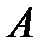 и
и 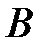 и обязательно благоприятствует
и обязательно благоприятствует  , но тогда
, но тогда 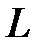 благоприятствует наступлению события
благоприятствует наступлению события 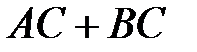 .
.
Аналогично, пусть L – благоприятствует наступлению 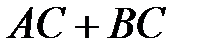 , тогда L благоприятствует хотя бы одному из событий AC и BC, следовательно, L благоприятствует C и хотя бы одному из
, тогда L благоприятствует хотя бы одному из событий AC и BC, следовательно, L благоприятствует C и хотя бы одному из 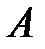 и
и 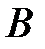 , тогда
, тогда 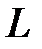 благоприятствует
благоприятствует 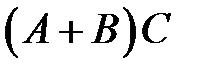 .
.
Итак, множество исходов опыта, благоприятствующих наступлению событий 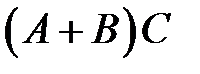 и
и 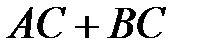 , совпадает, следовательно,
, совпадает, следовательно, 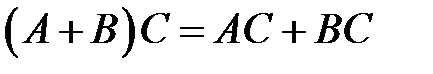 .
.
2. Kлассическое определение вероятности.
Вероятность события характеризует степень объективной возможности наступления этого события.
Если, в частности, множество  состоит из равновозможных элементарных событий, то вероятность
состоит из равновозможных элементарных событий, то вероятность
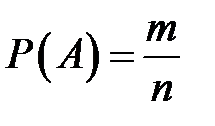 ,
,
где m – число благоприятных исходов A, n – число всех всевозможных исходов (классическое определение вероятности).
Из классического определения вероятности вытекают следующие ее свойства:
1. Вероятность достоверного события равна единице.
Действительно, число всех благоприятных исходов равно числу всех всевозможных исходов, т. е. m = n
P 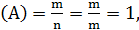
2. Вероятность невозможного события равна нулю.
Если событие невозможное, то число благоприятных исходов m = 0.
P 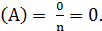
3. Вероятность случайного события есть положительное число, заключенное между 0 и 1.
0≤ P 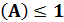 .
.
4. P 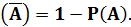
Пример 1.
В ящике 5 пронумерованных шаров с номерами от 1 до 5. Вынулиодин шар. Какова вероятность того, что номер вынутого шара не превышает 5.
Решение.
Так как номер шара не превышает 5, то число случаев, благоприятных событию A, равно числу всех случаев 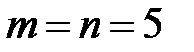 .
.
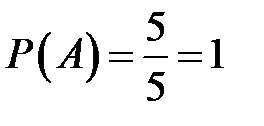 .
.
A – событие достоверное.
Пример 2.
Бросают две игральные кости. Какое событие более вероятно: сумма очков на выпавших гранях равна 11 или сумма очков на выпавших гранях равна 4?
Решение.
Поставим в соответствие исходу эксперимента упорядоченную пару чисел 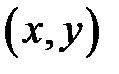 , где x – число очков выпавших на первой кости, а y – на второй.
, где x – число очков выпавших на первой кости, а y – на второй.
Пространство всех элементарных событий состоит из множества пар 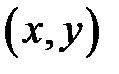 , где
, где 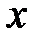 и
и 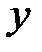 принимают значения от 1 до 6. Число таких пар 36. Событию A, состоящему в том, что сумма очков, выпавших на двух костях, равна 11, благоприятны два элементарных события
принимают значения от 1 до 6. Число таких пар 36. Событию A, состоящему в том, что сумма очков, выпавших на двух костях, равна 11, благоприятны два элементарных события 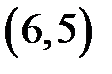 и
и 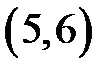 . Событию B, состоящему в том, что сумма очков, выпавших на двух костях равна 4, благоприятны три элементарных события, которым соответствуют
. Событию B, состоящему в том, что сумма очков, выпавших на двух костях равна 4, благоприятны три элементарных события, которым соответствуют 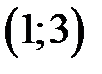 ,
, 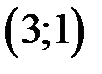 ,
,  .
.
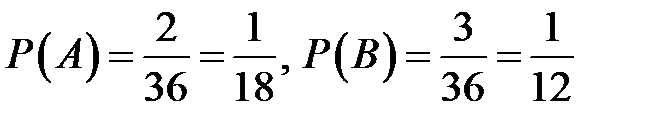 .
.
и, следовательно, событие 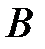 более вероятно.
более вероятно.
Пример 3.
Из 15 строительных рабочих 10 штукатуров, а 5 – маляры. Наудачу отбирается бригада 5 рабочих. Какова вероятность того, что среди них будет 3 маляра и 2 штукатура?
Решение.
Пространство элементарных событий состоит из различных выборок по 5 из 15. Число таких выборок равно 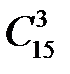 . Благоприятным событиям соответствуют выборки, содержащие трех маляров и двух штукатуров.
. Благоприятным событиям соответствуют выборки, содержащие трех маляров и двух штукатуров.
Трех маляров из пяти можно выбрать 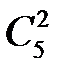 способами, а двух штукатуров из десяти
способами, а двух штукатуров из десяти 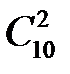 . Следовательно, число выборок, соответствующих благоприятным событиям, равно
. Следовательно, число выборок, соответствующих благоприятным событиям, равно 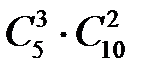 .
.
Таким образом 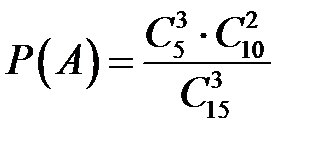 .
.
При классическом определении вероятности не всегда можно определить числа m и n для вычисления вероятностей событий, и поэтому непосредственно воспользоваться формулой 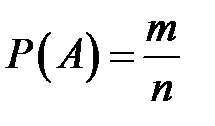 не удается.
не удается.
Геометрическая вероятность.
Например, пусть линия электропередач, соединяющая пункты A и B, в результате бури оборвались. Какова вероятность того, что обрыв произошел на участке, заключенном между пунктами C и D,принадлежащем отрезку AB?Множество элементарных событий в данном случае бесконечно, так как обрыв возможен в любой точке AB. При этом естественно предполагать, что вероятность обрыва на любом участке пропорциональна длине этого участка. Так как вероятность обрыва на всем AB равна 1, вероятность обрыва на CD выразится
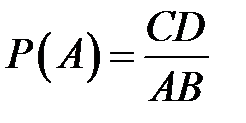 .
.
Геометрическое определение вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.)
Если обозначить меру (длину, площадь, объем) области через 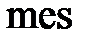 , то вероятность попадания точки, брошенной наудачу в область
, то вероятность попадания точки, брошенной наудачу в область 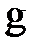 - часть области
- часть области  , равна
, равна 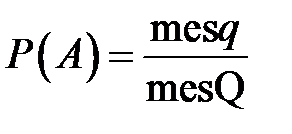
Пример 3.
Наудачу выбираются два действительных числа 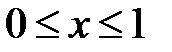 ,
, 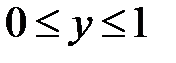 . Найти вероятность того, что
. Найти вероятность того, что 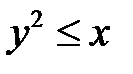 .
.
Решение.
Поставим в соответствие паре чисел 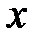 и
и 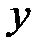 точку на плоскости
точку на плоскости 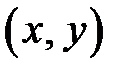 .
.
Пространство элементарных выборок будет квадрат, двумя сторонами которого являются единичные отрезки осей координат.
| y |
| x |
| y2=x |
Фигура, множество точек которой соответствует исходам, благоприятным событию 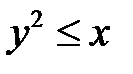 , ограничена графиками функций
, ограничена графиками функций 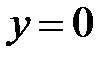 ,
, 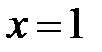 ,
, 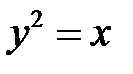 . Ее площадь
. Ее площадь 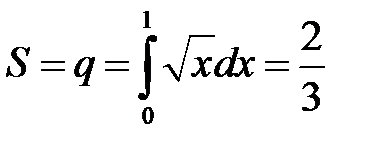 , а площадь квадрата равна единице.
, а площадь квадрата равна единице.
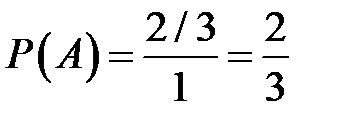 .
.
4. Вычисление вероятностей сложных событий.
Теоремы сложения и умножения вероятностей.
Условная вероятность
Теорема 1. (Сложения вероятностей)
Вероятность суммы двух совместных событий  и
и 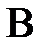 равна сумме вероятностей этих событий без вероятности их совместного наступления
равна сумме вероятностей этих событий без вероятности их совместного наступления
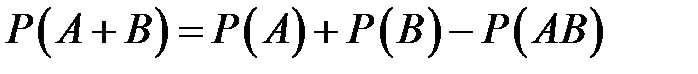 .
.
Вероятность суммы несовместных событий рвана сумме их вероятностей, т.е.
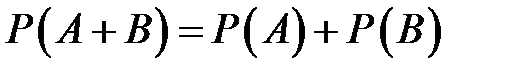 .
.
.
События 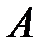 и
и 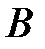 называются независимыми, если вероятность
называются независимыми, если вероятность 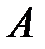 не зависит от того, произошло событие
не зависит от того, произошло событие 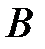 или нет.
или нет.
Событие 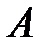 называется зависимым от события
называется зависимым от события 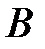 ,если вероятность события
,если вероятность события 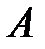 зависит от того, произошло или не произошло событие
зависит от того, произошло или не произошло событие 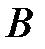 .
.
Вероятность события 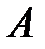 ,вычисленная при условии, что
,вычисленная при условии, что 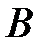 имело место, называется условной вероятностью
имело место, называется условной вероятностью 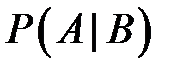 .
.
Теорема 2. (Умножения вероятностей)
Вероятность произведения двух зависимых событий 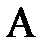 и
и 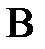 равна произведению вероятности одного их этих событий на условную вероятность другого, при условии, что первое наступило:
равна произведению вероятности одного их этих событий на условную вероятность другого, при условии, что первое наступило:
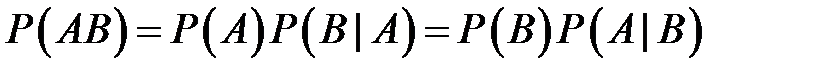 .
.
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:
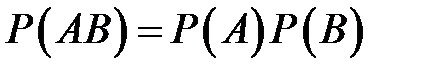 .
.
Пример 1.
Три стрелка независимо друг от друга стреляют по цели Вероятность попадания в цель для первого стрелка − 0,75; для второго − 0,3; для третьего − 0,9. Найти вероятность того, что все три стрелка попадут в цель.
Решение.
Пусть событие 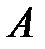 – первый стрелок попал в цель; событие
– первый стрелок попал в цель; событие 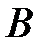 – второй стрелок попал вцель; событие
– второй стрелок попал вцель; событие  – третий стрелок попал в цель;
– третий стрелок попал в цель;
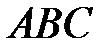 – все три стрелка попадут в цель.
– все три стрелка попадут в цель.
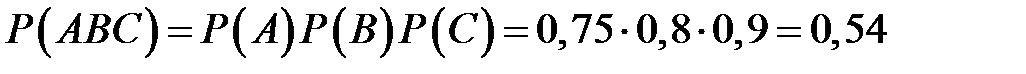 .
.
Пример 2.
Идет бомбардировка трех складов боеприпасов. Сбрасывают одну бомбу. Вероятность попадания в первый склад равна 0,01; во второй равна 0,008; в третий − 0,025. При попадании в любой их них взрываются все. Найти вероятность того, что склады будут взорваны.
Решение.
Событие 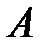 – взрыв складов;
– взрыв складов; 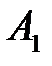 – попадание в первый склад;
– попадание в первый склад; 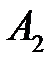 – попадание во второй склад;
– попадание во второй склад; 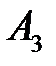 – попадание и третий склад.
– попадание и третий склад.
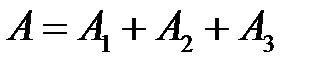 , так как
, так как 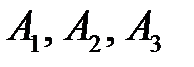 несовместны, то:
несовместны, то:
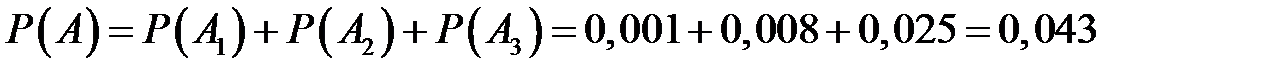 .
.
Пример 3.
Имеется три ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение.
Вероятность того, что из первого ящика вынута стандартная деталь (событие А) равна 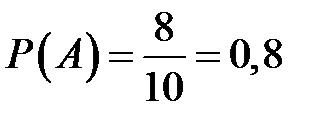 .
.
Вероятность того, что из второго ящика вынута стандартная деталь (событие В) равна 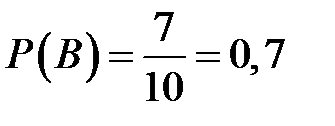 .
.
Вероятность того, что из третьего ящика вынута стандартная деталь (событие C) равна 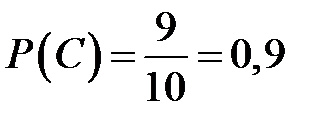 .
.
Так как события 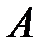 ,
, 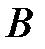 и
и  независимы, то искомая вероятность события
независимы, то искомая вероятность события  (по теореме умножения) равна
(по теореме умножения) равна
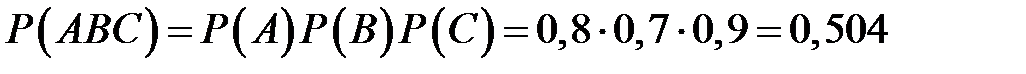 .
.
Пример 4.
Вероятности появления каждого из трех независимых событий 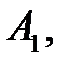
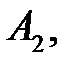
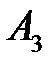 соответственно равны
соответственно равны 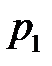 ,
, 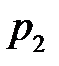 ,
, 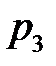 Найти вероятность появления только одного из этих событий.
Найти вероятность появления только одного из этих событий.
Решение.
Заметим, что, например, появление только первого события 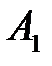 , равносильно появлению события
, равносильно появлению события  (появилось первое и не появились второе и третье события).
(появилось первое и не появились второе и третье события).
Обозначим:
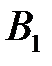 – появление только события
– появление только события 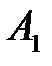 , т.е.
, т.е. 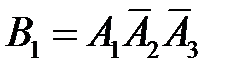 ;
;
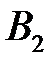 – появление только события
– появление только события 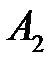 , т.е.
, т.е. 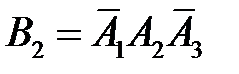 ;
;
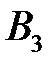 – появление только события
– появление только события 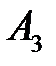 , т.е.
, т.е. 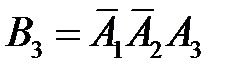 .
.
Таким образом, чтобы найти вероятность появления только одного из событий 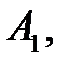
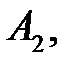
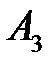 , воспользуемся теоремой сложения несовместных событий:
, воспользуемся теоремой сложения несовместных событий: 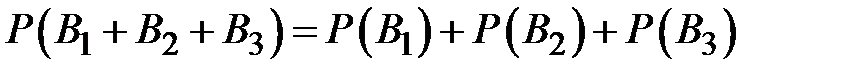 .
.
Определим вероятности каждого из событий 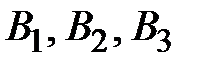 .
.
События 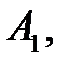
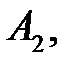
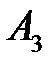 – независимы, поэтому
– независимы, поэтому
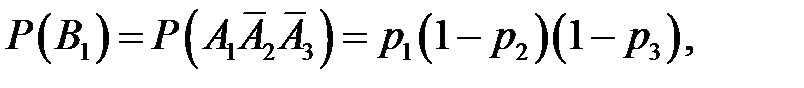
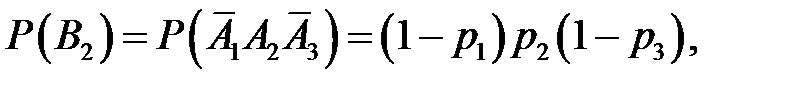
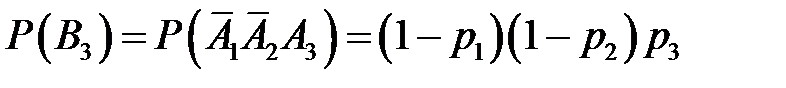 ,
,
и тогда
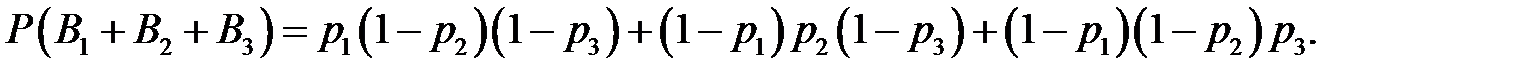
Пример 5.
Вероятность попадания в цель при стрельбе изтрех орудий соответственно равны 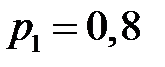 ,
, 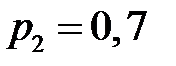 ,
, 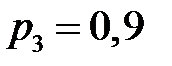 . Найти вероятность хотя бы одного попадания (событие A) при одном залпе из всех орудий.
. Найти вероятность хотя бы одного попадания (событие A) при одном залпе из всех орудий.
Решение.
Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий.
Рассмотрим события;
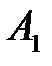 – попадание первым орудием;
– попадание первым орудием;
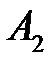 – попадание вторым орудием;
– попадание вторым орудием;
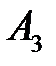 – попадание третьим орудием.
– попадание третьим орудием.
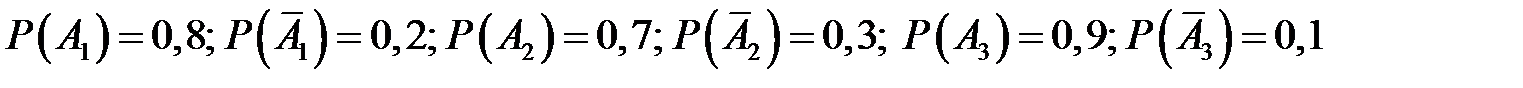 ;
;
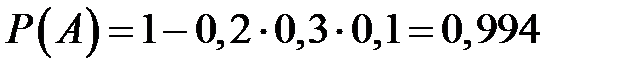 .
.
Пусть событие 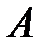 – хотя бы одно попадание, а
– хотя бы одно попадание, а 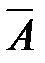 – ни одного попадания, тогда
– ни одного попадания, тогда 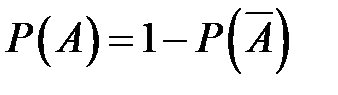 .
.
Событие 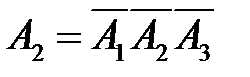 , тогда
, тогда 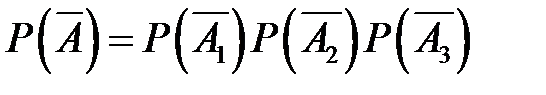 .
.
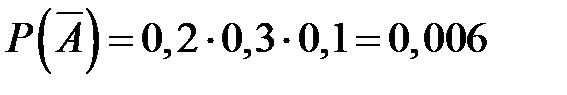 и
и 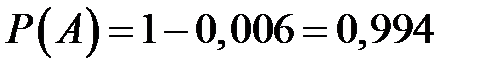 .
.
Пример 6.
Бросаются две монеты. Рассматриваются события: A – выпадение герба на первой монете, B – выпадение герба на второй монете. Найти вероятность события 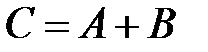 .
.
Решение.
Так как события A и B – совместны, то
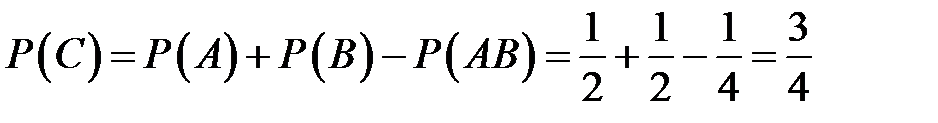 ,
,
или через противоположное событие
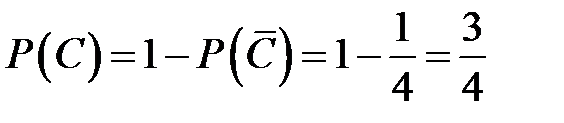 .
.
.
5. Формула полной вероятности и формула Байеса
Пусть рассматривается полная группа событий 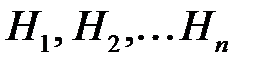 (попарно несовместные, которые называются гипотезами), и если событие
(попарно несовместные, которые называются гипотезами), и если событие 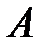 может наступить только при появлении одной их этих гипотез, то вероятность события
может наступить только при появлении одной их этих гипотез, то вероятность события 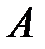 вычисляется по формуле полной вероятности:
вычисляется по формуле полной вероятности:
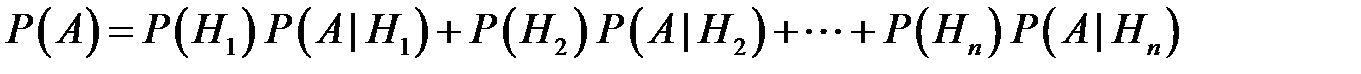 ,
,
или
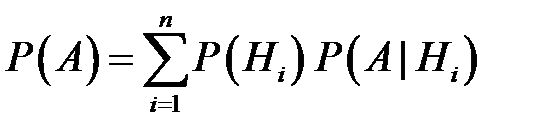 ,
,
где 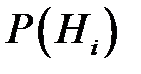 – вероятность гипотезы
– вероятность гипотезы 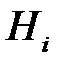 ,
, 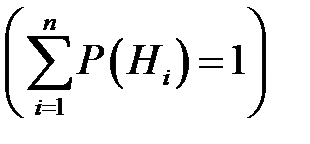 .
.
Пример 1.
Для приема зачета преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 задач по интегральному исчислению.
Для сдачи зачета студент должен решить первую же наудачу
доставшуюся задачу. Какова вероятность для студента сдать зачет, если он умеет решать 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение.
Пусть событие А – студент сдал зачет. Сформулируем гипотезы:
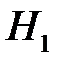 – получил задачу по дифференциальному исчислению;
– получил задачу по дифференциальному исчислению;
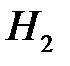 – получил задачу по интегральному исчислению;
– получил задачу по интегральному исчислению;
Р(Н1) = 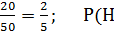 2) =
2) = 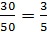 ;
; 
P(A| 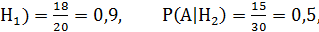
по формуле полной вероятности9
P(A) = Р(Н1) P(A| 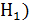 +
+ 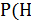 2)
2) 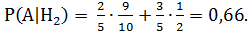
Пример 2.
Имеется три одинаковые урны. В первой a белых шаров и b черных; во второй – c белых и d черных; в третьей только белые шары. Некто подходит наугад к одной из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.
Решение.
Пусть событие A – появление белого шара. Формулируем гипотезы:
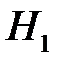 – выбор первой урны;
– выбор первой урны;
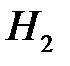 – выбор второй урны;
– выбор второй урны;
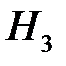 – выбор третьей урны;
– выбор третьей урны;
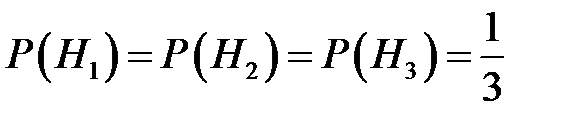 ,
,
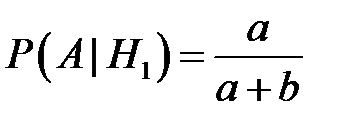 ,
, 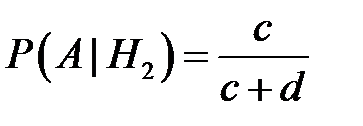 ,
, 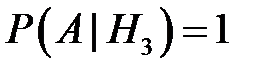 ;
;
по формуле полной вероятности
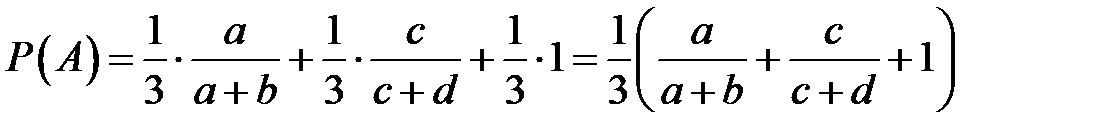 .
.
Следствием теоремы умножения и формулы полной вероятности является так называемая теорема гипотез, или формула Бейеса.
∙соответственно P( 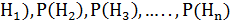 , а в результате опыта появилось событие А, то с учетом этого события изменились вероятности гипотез. Надо найти теперь условные вероятности Р(
, а в результате опыта появилось событие А, то с учетом этого события изменились вероятности гипотез. Надо найти теперь условные вероятности Р( 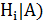 для каждой из гипотез, которые вычисляются по формуле Бейеса:
для каждой из гипотез, которые вычисляются по формуле Бейеса:
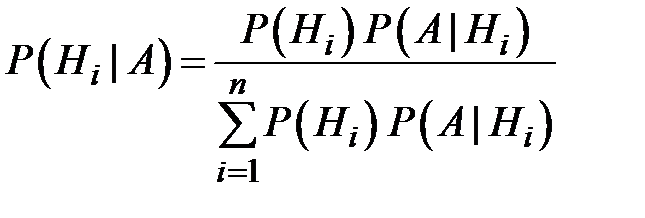 .
.
Формула Байеса дает возможность переоценить вероятности гипотез с учетом уже известного результата опыта.
Пример 1.
Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8 а для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.
Решение.
Пусть событие А – мишень поражена первым стрелком.
Рассмотрим следующие гипотезы:
Н1 – оба стрелка не попали;
Н2 – попали оба стрелка;
Н3 – первый стрелок попал, второй стрелок не попал;
Н4 – второй стрелок попал, первый стрелок не попал.
Найдем вероятности гипотез:
Р(Н1) = 0,2∙0,6 = 0,12, Р(Н2) = 0,4∙0,8 = 0,32, Р(Н3) = 0,8∙0,6 = 0,48,
Р(Н4) = 0,4∙0,2 = 0,08. 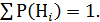
Найдем условные вероятности события А
Р(A|H1) = 0, P(A|H2) = 0, P(A|H3) = 1, P(A|H4) = 1.
Найдем вероятность, что мишень поражена первым стрелком
P(H3|A) = 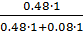 =
= 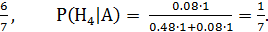
Пример 2.
В урне лежит шар неизвестного цвета, с равной вероятностью белый или черный. В урну опустили один белый шар и тщательно перемешали. Наудачу извлекли один шар. Он оказался белым. Какова вероятность, что в урне остался белый шар?
Решение.
Пусть событие А – в урне лежит белый шар.
Рассмотрим следующие гипотезы:
Н1 –лежит белый шар;
Н2 –лежит черный шар.
Найдем вероятности гипотез:
Р(Н1) = 0,5; Р(Н2) = 0,5.
Условные вероятности события А:
Р(А| H1) = 1; P(A|H2) =  .
.
По формуле Бейеса находим:
Р(Н1|A) = 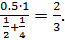
6. Повторение опытов
Если производится n независимых опытов в одинаковых условиях, причем в каждом из них с вероятностью p происходит событие A, то вероятность 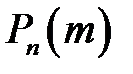 того, что событие
того, что событие 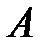 произойдет в этих n опытах ровно m раз, выражается формулой:
произойдет в этих n опытах ровно m раз, выражается формулой:
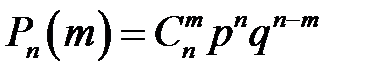 ,
,
где 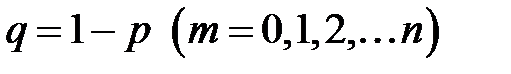 , которая называется формулой Бернулли.
, которая называется формулой Бернулли.
Вероятность появления хотя бы одного события A при n независимых опытах в одинаковых условиях равна 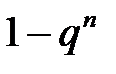 .
.
Вероятность того, что событие наступит а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз находим соответственно но формулам:
а) 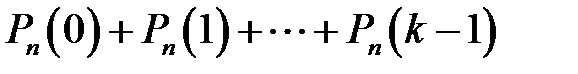 ;
;
б) 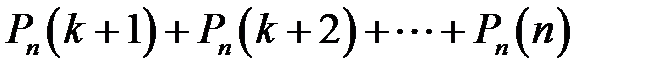 ;
;
в) 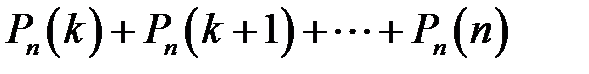 ;
;
г) 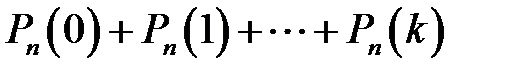 .
.
Пример 2.
В урне 30 белых и 15 черных шаров. Вынули подряд 5 шаров, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из 5 вынутых шаров окажется 3 белых.
Решение.
Вероятность извлечения белого шара 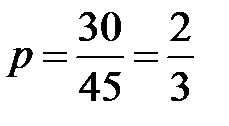 , можно посчитать одной и той же во всех 5 испытаниях. Тогда вероятность не появления белого шара равна
, можно посчитать одной и той же во всех 5 испытаниях. Тогда вероятность не появления белого шара равна 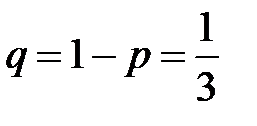
Используя формулу Бернулли получаем:
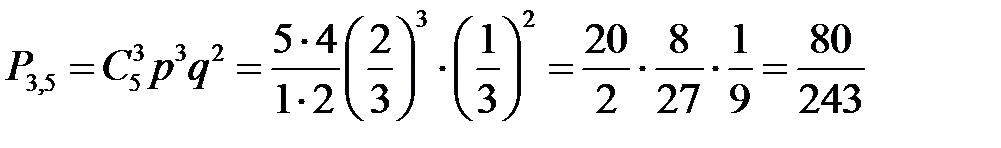 .
.
Ответ: 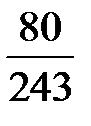 .
.
Пример 3.
Монету подбрасывают восемь раз. Какова вероятность того, что шесть раз она упадет гербом вверх?
Решение.
Имеем схему испытаний Бернулли. Вероятность появления герба в одном испытании 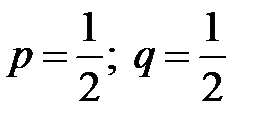 , тогда
, тогда
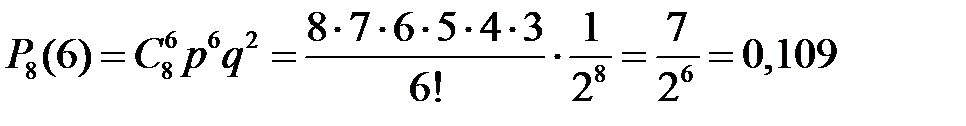 .
.
Ответ: 0,109.
Пример 4.
Производится четыре независимых выстрела, причем 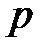 – вероятность попадания в мишень есть среднее из вероятностей
– вероятность попадания в мишень есть среднее из вероятностей 
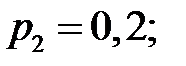
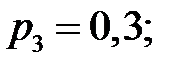
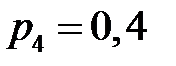 . Найти вероятности:
. Найти вероятности: 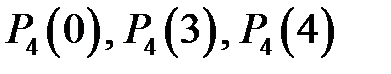 .
.
Решение.
Найдем
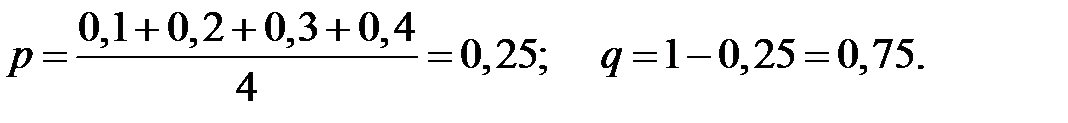
По формуле Бернулли имеем:
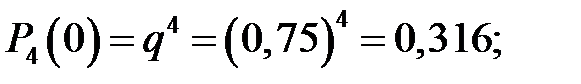
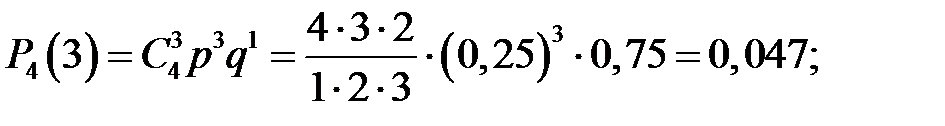
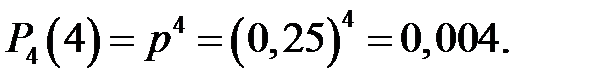
Пример 5.
Имеется пять станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций друг от друга перерыв связи с каждой из них происходит независимо от остальных с вероятностью 0,2. Найти вероятность того, что в данный момент времени будет поддерживаться связь не более чем с двумя станциями.
Решение.
Событие 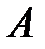 – имеется связь не более чем с двумя станциями.
– имеется связь не более чем с двумя станциями.
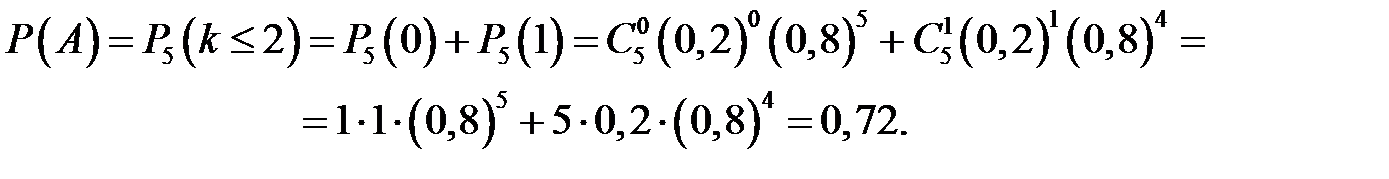
Ответ: 0,72.
Пример 6.
Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из десяти единиц. Каждый из объектов может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один из объектов будет потерян.
Решение.
формуле:
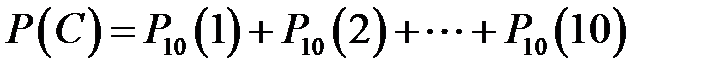 ,
,
но проще воспользоваться вероятностью противоположного события – ни один объект не потерян – и вычесть ее из единицы
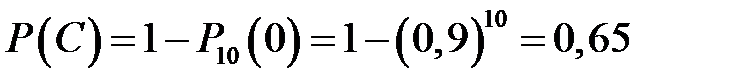 .
.
Ответ: 0,65.
Непосредственное применение формулы Бернулли пи большом числе испытаний связано с громоздкими вычислениями. Поэтому при больших n вместо нее, как правило, используют приближенные формулы Пуассона, Муавра –Лапласа.
Формула Пуассона.
Если число испытаний n достаточно велико, а вероятность 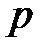 достаточно мала, причем произведение a=np не мало и не велико ( обычно достаточно условий p≤0,1; npq<10), то вероятность
достаточно мала, причем произведение a=np не мало и не велико ( обычно достаточно условий p≤0,1; npq<10), то вероятность 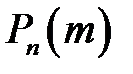 можно приближенно вычислить по формуле Пуассона
можно приближенно вычислить по формуле Пуассона
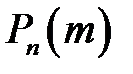 ≈
≈ 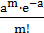
Пример.
Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится , равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение.
n=5000, p = 0,0002, m = 3, a = 5000∙0,0002 = 1.
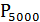 (3) =
(3) =  =
= 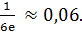
8.Локальна формула Муавра – Лапласа.
Теорема. Если число испытаний n достаточно велико, а вероятности 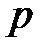 и q не очень близки к нулю ( обычно достаточно условий n>100, npq>20), то вероятность
и q не очень близки к нулю ( обычно достаточно условий n>100, npq>20), то вероятность 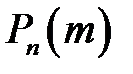 можно приближенно найти по локальной формуле Муавра – Лапласа
можно приближенно найти по локальной формуле Муавра – Лапласа
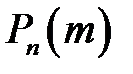 ≈
≈ 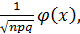 x =
x = 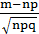 , φ(x) =
, φ(x) = 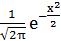 - функция Гаусса.
- функция Гаусса.
Имеются таблицы, в которых помещены значения функции φ(x) = 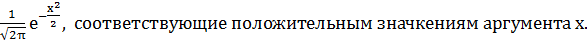
Для отрицательных значений аргумента х пользуются теми же
таблицами, так как φ(х) – четная, т.е. φ(-х) = φ(х).
Итак, вероятность того, что событие А появится в n независимых испытаниях ровно m раз, приближенно равно
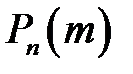 ≈
≈ 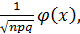 x =
x = 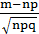 .
.
Пример.
Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение.
По условию, n =10, m = 8 p = 0,75, q = 1 -0,75 = 0,25.
Воспользуемся локальной формулой ( или асимптотической ) Лапласа
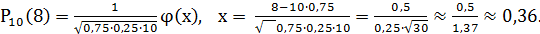
φ(0,36) = 0,3739, 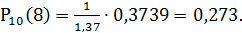
9. Интегральная формула Муавра – Лапласа.
Вновь предположим, что производится n испытаний , в которых вероятность появления события А постоянна и равна 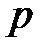 . Как вычислить вероятность
. Как вычислить вероятность 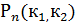 того, что событие А появится в n испытаниях не менее
того, что событие А появится в n испытаниях не менее 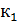 и не более
и не более 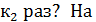 этот вопрос отвечает интегральная теорема Муавра- Лапласа.
этот вопрос отвечает интегральная теорема Муавра- Лапласа.
Теорема. В условиях интегральной формулы Муавра-Лапласа вероятность
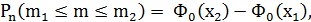 где
где
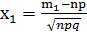 ,
, 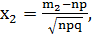
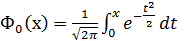 - функция Лапласа.
- функция Лапласа.
При решении задач, требующих применения интегральной формулы Муавра – Лапласа , используют специальные таблицы, так как определенный интеграл не выражается через элементарные функции.
Таблицы даны для положительных значений х и для х=0. Для х<0, пользуются ими же, учитывая , что Ф(-х) = - Ф(х).
Пример. Вероятность наступления события А в данном испытании равна 0,5. Найти вероятность того, что событие А наступит от 500 раз до 530 раз в 1000 испытаниях.
Решение.
n = 1000, p = 0,5, 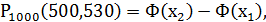
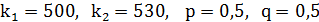 ,
,
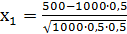 = 0,
= 0, 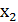 =
= 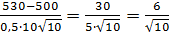 =
= 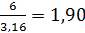
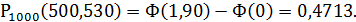 |
10. Случайные величины
Определение.Случайной величиной называют переменную величину, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Примеры: Число появления герба при трех бросаниях монеты.
Случайные величины обозначают прописными буквами X,Y,Z,…, аих возможные значения – x,y,z,…
Дискретной случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать.
Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.
Ряд распределения ( закон распределения)
Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется рядом распределения:
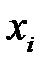 |  | 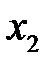 | 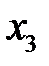 | … |  | 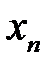 |
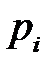 | 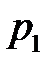 | 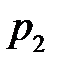 | 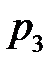 | … | 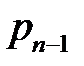 | 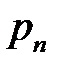 |
где 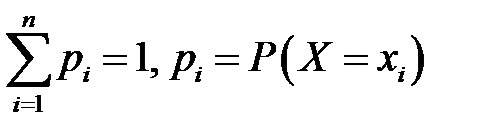 .
.
Графическое изображение ряда распределения называется многоугольником распределения.
| xi |
| pi |
| x4 |
| x3 |
| x2 |
| x1 |
| x5 |
| x6 |
Пример.
Стрелок ведет стрельбу по мишени до первого попадания, имея боезапас 4 патрона. Вероятность попадания при каждом выстреле равна 0,6. Построить ряд распределения боезапаса, оставшегося неизрасходованным.
Решение.
Случайная величина Х – число неизрасходованных патронов имеет четыре возможных значения:0,1,2,3.
Строим ряд распределения вероятностей:
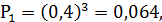
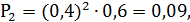
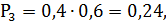
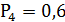
11.Функция распределения
Ряд распределения не является исчерпывающей характеристикой, он существует только для дискретных случайных величин, для непрерывной случайной величины такой характеристики построить нельзя.
Функцией распределения случайной величины 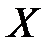 называется функция
называется функция 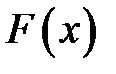 ,выражающая вероятность того, что
,выражающая вероятность того, что  принимает значения меньше, чем
принимает значения меньше, чем 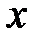 :
: 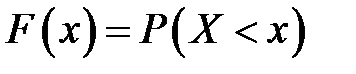 .
.
Свойства 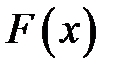 :
:
1) 0≤ F(x) ≤ 1;
2) Функция  есть неубывающая функция;
есть неубывающая функция;
3) 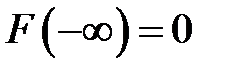 ;
;
4)  ;
;
5) Для дискретных случайных величин 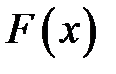 есть разрывная ступенчатая функция, непрерывная слева.
есть разрывная ступенчатая функция, непрерывная слева.
Пример 1.
Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле 0,3. Построить ряд распределения числа попаданий.
Решение.
Строим ряд распределения вероятностей, используя формулу: 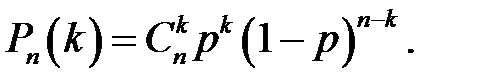
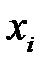 | 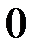 | 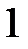 | 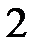 | 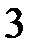 |
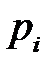 | 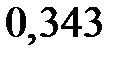 |  | 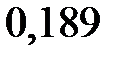 | 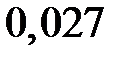 |
Пример 2.
Случайная величина 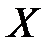 задана рядом распределения
задана рядом распределения
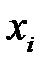 | ||||
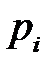 | 0,14 | 0,20 | 0,49 | 0,17 |
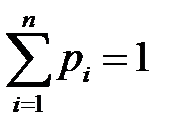 .
.
Найти функцию распределения случайной величины X и построить ее график.
Решение.
1. Если 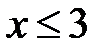 , то
, то 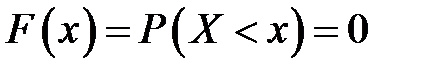 .
.
2. Если 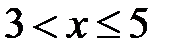 , то
, то 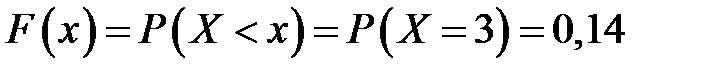 .
.
3. Если 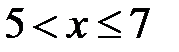 , то
, то
 .
.
4. Если 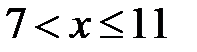 , то
, то
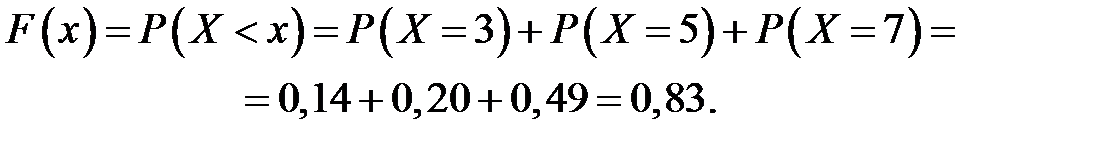
5. Если 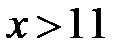 , то
, то
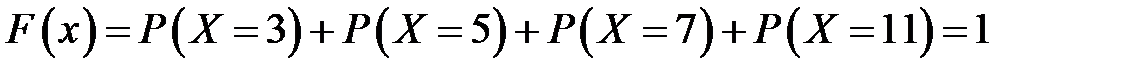 .
.
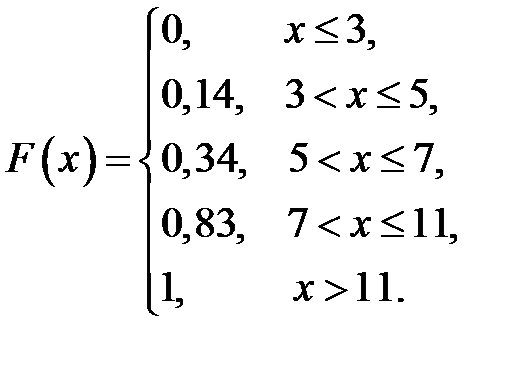
Строим график.
| 0,14 |
| F(x) |
| x |
12.Числовые характеристики дискретных случайных величин
Закон распределения полностью задает дискретную случайную величину. Однако часто встречаются случаи, когда закон распределения случайной величины неизвестен. В таких случаях случайную величину изучают по ее числовым характеристикам. Одной из таких характеристик является математическое ожидание.
Пусть некоторая случайная величина Х с конечным числом своих значений задана законом распределения:
| Х |  | 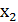 | ……. | 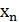 |
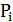 | 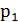 | 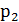 | ……. | 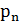 |
Определение. Математическим ожиданием дискретной случайной величины 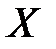 называют сумму произведений всех возможных значений величины Х на соответствующие вероятности, или ( ее среднее значение), вычисляемое по формуле:
называют сумму произведений всех возможных значений величины Х на соответствующие вероятности, или ( ее среднее значение), вычисляемое по формуле:
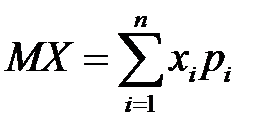 =
=  +….+
+….+  .
.
Пример 1.
Случайная величина 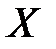 – число очков, выпавших при однократном бросании игральной кости. Определить M(X).
– число очков, выпавших при однократном бросании игральной кости. Определить M(X).
Решение.
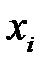 | ||||||
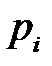 | 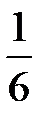 | 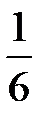 | 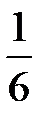 | 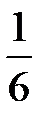 | 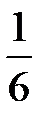 | 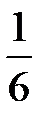 |
Имеем
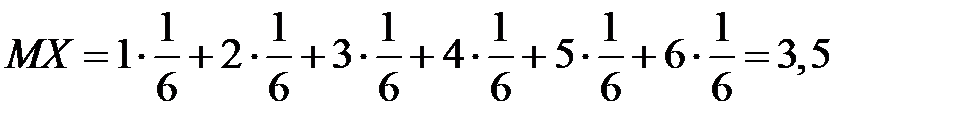 ;
;
Свойства математического ожидания.
1.Математическое ожидание постоянной величины С равно этой величине.
2.Постоянный множитель можно выносить за знак математического ожидания, т.е. М(СХ) = СМ(Х).
3.Математическое ожидание суммы двух случайных величин X и Y равно сумме их математических ожиданий:
M(X+Y) = M(X) + M(Y)
Определение.Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое возможное значение приняла другая величина.
Пример двух независимых случайных величин – суммы выигрыща по каждому из двух билетов по двум различным денежно-вещевым лотереям.
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) = M(X)∙M(Y)
5. Математическое ожидание разности двух случайных величин X и Y равно разности их математических ожиданий:
M(X-Y) = M(X) – M(Y).
Пример 1.
Найти математическое ожидание случайной величины Z = X + 2Y, если известны математические ожидания случайных величин X и Y M(X) = 5, M(Y) = 3.
Пример 2.
Независимые случайные величины заданы законами распределения:
| Х | |||
| Р | 0,2 | 0,6 |
| Y | 0,5 | ||
| Р | 0,4 | 0,1 |
Найти математическое ожидание М(YХ).
