ГЛАВА 5. Устойчивость систем регулирования

Всякая АСР, которая подвергается внешнему воздействию, отклоняется от заданного ей закона движения. При этом регулятор стремится вернуть систему к этому движению. В результате под влиянием воздействий, с одной стороны, и восстанавливающего действия регулятора, с другой, возникает переходный процесс.

В этой ситуации возможны три случая:

1) система регулирования не может восстановить требуемого движения после его нарушения и действительное движение системы будет все дальше удалятся от требуемого. Такой переходный процесс называется расходящимся, а система – неустойчивой.

2) система регулирования после нарушения движения воздействиями с течением времени возвращается к заданному движению с точностью, отвечающей статической неравномерности (ошибки) системы регулирования. Такой переходный процесс будет сходящимся, а система – устойчивой.

3) система регулирования после нарушения равновестного режима получает дополнительно к заданному движению еще и установившееся периодическое движение, которое представляет собой незатухающие колебания. Такой переходный процесс называется незатухающим колебательным, а система находящейся на границе устойчивости.

Движение большинства реальных АСР описывается нелинейными дифференциальными уравнениями, которые для упрощения исследования АСР могут быть линеаризированы. На их основе составляется дифференциальное уравнение замкнутой системы с регулируемой величиной в качестве переменной

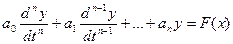, (5-1)

которое представляет собой неоднородное дифференциальное уравнение, характеризующее динамические свойства системы при наличии в ней внешних воздействий.

Решение этого уравнения можно представить в виде двух составляющих.

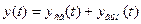(5-2)

описывающих свободные и вынужденные колебания системы, при этом 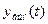определяется неснимающимся воздействием, приложенным к АСР.

Для получения решения уравнения (5-1) достаточно к какому-либо частному решению прибавить общее решение однородного с ним уравнения, т.е. уравнения (5-1) в котором .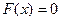

Его характеристическое уравнение в операторной форме имеет вид:

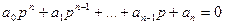, (5.3)

где 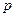- корни характеристического уравнения.

Оно получается, если приравнять нулю собственный оператор – оператор левой части неоднородного дифференциального уравнения 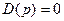. Для замкнутой системы при отсутствии внешнего воздействия характеристическое уравнение может быть получено по передаточной функции системы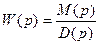

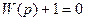(5.4)

При исследованиях устойчивости динамической системы в уравнение движения не вводится внешнее воздействие 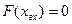, а рассматриваются собственные колебания системы относительно состояния установившегося движения.

Такое исследование принято называть исследованием в малом, в отличие от исследования в большом, когда анализируется поведение системы при достаточно больших отклонениях регулируемой величины от заданного значения.

Решению задач об устойчивости систем посвящено большое количество трудов многих выдающихся ученых, среди которых первое место по праву принадлежит русскому математику Александру Михайловичу Ляпунову, создавшего общий метод решения задач об устойчивости.

Теорема Ляпунова.

А.М. Ляпунов при исследовании устойчивости динамических систем пришел к следующим выводам относительно законности использования линеаризованных дифференциальных уравнений для суждения об устойчивости действительной системы в малом.

1) Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то действительная система будет устойчива. При этом никакие отброшенные при линеаризации уравнения члены второй и высших степеней отклонения регулируемого параметра не могут изменить устойчивость системы.

2) Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то действительная система будет неустойчива. При этом никакие отброшенные при линеаризации члены второй и высших степеней отклонения регулируемого параметра не могут придать устойчивость системе.

3) Если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или пару чисто мнимых сопряженных корней, то поведение действительной системы не может определяться ее линеаризованным уравнением. В этих случаях отброшенные при линеаризации уравнения члены вторых и высших степеней отклонения регулируемого параметра коренным образом изменяют описание динамического процесса реальной системы.

Следует отметить, что приведенная теорема Ляпунова об устойчивости линеаризованных систем справедлива только тогда, когда у нелинейной системы функция, выражающая зависимость регулируемой величины от переменных параметров имеет конечные, непрерывные и однозначные производные в окрестности точки, относительно которой исследуется процесс регулирования.

Если динамика системы точно описывается линейным дифференциальным уравнением с постоянными коэффициентами, то устойчивость в малом обеспечивает неограниченную устойчивость системы, т.е. устойчивость в большом независимо от величины отклонения.

Относительно систем, движение которых описывается нелинейными дифференциальными уравнениями, этого сказать нельзя. Возможны случаи, когда система, устойчивая в малом, оказывается неустойчивой в большом. Поэтому методы исследования устойчивости нелинейных систем существенно отличается от методов исследования линейных систем.

Если отложить в прямоугольных координатах плоскости корней по оси абсцисс вещественные части, а по оси ординат – коэффициенты при мнимых частях корней характеристического уравнения, то в этой плоскости каждому корню будет соответствовать точка. Вещественные корни определяют точки на оси абсцисс, а пара сопряженных комплексных корней две точки, расположенные симметрично относительно оси абсцисс.

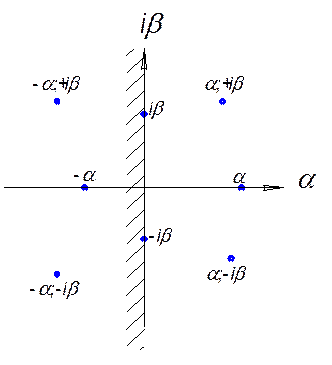
Рис 5.1 Плоскость корней характеристического уравнения.

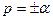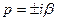1) , 2) , 3)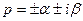

Таким образом, для того чтобы действительная система была устойчива, необходимо и достаточно, чтобы корни характеристического уравнения линеаризованной системы находились в комплексной плоскости корней слева от мнимой оси. Если хотя бы одна точка лежит на мнимой оси, то система находится на границе устойчивости. Следовательно, для суждения об устойчивости АСР нет необходимости вычислять все корни характеристического уравнения, достаточно лишь выяснить, все ли они расположены слева от мнимой оси.

Однако уравнения степени выше четвертой не решаются в радикалах. Таким образом, возникает необходимость иметь признаки, которые позволили бы без решения характеристического уравнения, во-первых, проверить устойчивость конкретной АСР, а во-вторых, определили бы необходимые и достаточные условия для того чтобы переходные процессы в АСР протекали устойчиво.

При исследовании устойчивости возможны две постановки задачи для определения устойчивости системы. Первая сводится к тому, что если известны все заданные конструктивные и настроечные параметры системы, то нужно определить будет ли система устойчива. Решение этой задачи достигается с помощью использования критериев устойчивости.

Вторая постановка предполагает известными некоторые параметры, например, конструктивные. Решение этой задачи сводится к определению пределов изменения остальных параметров, например, настроечных, обеспечивающих устойчивость исследуемой системы, что достигается построение областей устойчивости.