Векторное произведение векторов

Упорядоченная тройка некомпланарных векторов 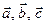называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки; в противном случае тройка называется левой (рис. 4.1).

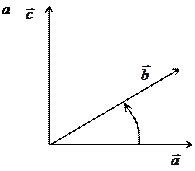
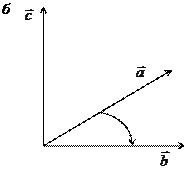
Рис. 4.1: а – тройка 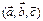правая; б – тройка 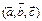левая

Векторным произведением вектора 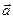на вектор 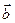называется вектор 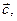удовлетворяющий условиям:

1) 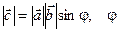– угол между векторам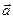и и ;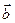

2)

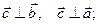
3) Упорядоченная тройка 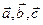– правая.

Обозначение: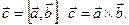

Свойства векторного произведения

1)

2)

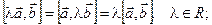
3)

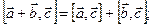
4) 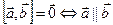– условие коллинеарности векторов.

Если векторы 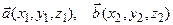заданы своими коорди-натами в ортонормированном базисе , то

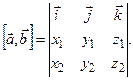
Площадь параллелограмма, построенного на векторах мож-но определить по формуле

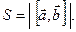
Пример 4.5. Найти площадь и длину высоты BD треугольника с вершинами в точках А(1, –2, 8), В(0, 0, 4), С(6, 2, 0).

Решение. Поскольку площадь S треугольника АВС равна 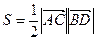, то .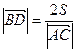

Рис. 4.2

1. Находим координаты векторов и длину 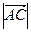вектора :

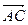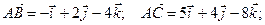
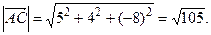
2. Находим S:

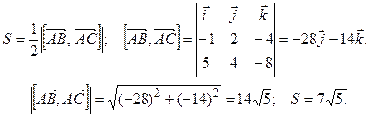
3.

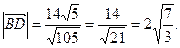
Механический смысл векторного произведения. Пусть точка А твердого тела закреплена, а в его точке В приложена сила 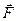. Тогда возникает вращательный момент 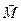(момент силы). По определению момент силы относительно точки А находится по формуле .

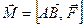Смешанное произведение векторов

Смешанным произведением трех векторов 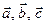называется число, получаемое следующим образом: векторное произведение 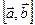умножается скалярно на вектор 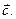Смешанное произведение векторов 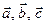обозначается 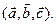Таким образом, 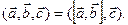Если векторы 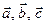заданы своими координатами в ортонормированном базисе, то

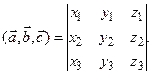
Объем параллелепипеда V, построенного на векторах 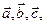можно вычислить по формуле 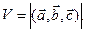Для того чтобы три вектора 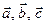были компланарны, необходимо и достаточно, чтобы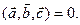

Пример 4.6. Вычислить объем треугольной пирамиды с вершинами А(0, 0, 1), В(2, 3, 5), С(6, 2, 3), D(3, 7, 2).

Решение. Рассмотрим три вектора

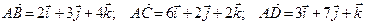(рис. 4.3).

Можно показать, что объем пирамиды АВСD равен шестой части объема параллелепипеда, построенного на векторах

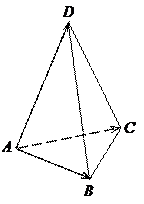
Рис. 4.3

Тогда 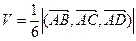, а так как

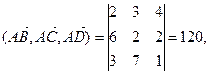то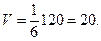

Прямая на плоскости. Плоскость

Прямая на плоскости.

В декартовой прямоугольной системе координат Оxy прямая на плоскости может быть задана уравнениями:

– общее уравнение прямой

Ax + By + C = 0; (4.3)

– уравнение прямой, проходящей через точку M₀(x₀, y₀)перпендикулярно нормальному вектору :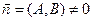

A(x – x₀) + B(y – y₀) = 0;

– уравнение прямой, проходящей через точку M₀(x₀, y₀)параллельно направляющему вектору 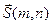(каноническое уравнение прямой):

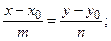
– параметрические уравнения прямой

;

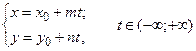– уравнение прямой в отрезках

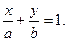
Здесь a и b – величины отрезков, отсекаемых на осях координат Ox и Oy (т.е. длины, взятые с соответствующими знаками);

– уравнение прямой, проходящей через две данные точки M₁(x₁, y₁) и M₂(x₂, y₂):

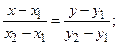
– уравнение прямой с угловым коэффициентом k, проходящей через точку M₀(x₀, y₀):

y – y₀ = k(x – x₀).

Расстояние 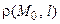от точки M₀(x₀, y₀) до прямой l, заданной уравнением (4.3), определяется по формуле

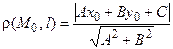. (4.4)

Две прямые, заданные уравнениями A₁x + B₁y + C₁ = 0и A₂x +
+ B₂y + C₂ = 0, параллельны, если 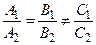, и перпендикулярны, если A₁A₂ + B₁B₂ = 0.

Пример 4.7. Составить уравнение прямой на плоскости, проходящей через точку М(–1, 2) перпендикулярно вектору, проходящему через точки М₁(3, 1) и М₂(4, –2). Найти расстояние от точки М до прямой, проходящей через точки М₁и М₂.

Решение. Уравнение прямой запишем в виде:

A(x – x₀) + B(y – y₀) = 0,

где x₀, y₀– координаты точки М, а А и В – координаты нормального вектора.

Так как 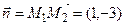, то уравнение имеет вид 1(x + 1) –
– 3(y – 2) = 0 или x – 3y + 7 = 0.

Для нахождения расстояния от точки М до прямой М₁М₂ запишем уравнение этой прямой в виде

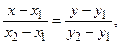т.е. ,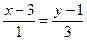

или 3x + y – 10 = 0.

Подставляя в формулу (4.4) координаты x₀ = –1, y₀ = 2 точки М, получаем

.

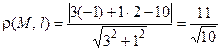2. Плоскость. Плоскость в прямоугольной системе координат мо-жет быть задана уравнениями:

Ax + By + Cz + D = 0 – общее уравнение плоскости. (4.5)

Если в уравнении (4.5) отсутствует свободный член D, то плоскость проходит через начало координат; если в уравнении (4.5) отсутствует одна из переменных, то плоскость параллельна той оси, название которой не входит в это уравнение;

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0 –

уравнение плоскости, проходящей через точку М₀(x₀, y₀, z₀) перпендикулярно нормальному вектору ;

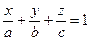– уравнение плоскости в отрезках,

где а, b, c – величина отрезков, отсекаемых плоскостью на координатных осях;

– уравнение плоскости, проходящей через три данные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃):

(4.6)

Величина угла φмежду двумя плоскостями A₁x + B₁y + C₁z + D₁ = 0 и A₂x + B₂y + C₂z +D₂ = 0 вычисляется по формуле

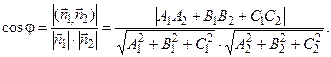
Условие перпендикулярности данных плоскостей запишется в виде

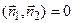или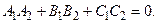

Условие параллельности рассматриваемых плоскостей имеет вид

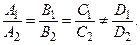
Расстояние 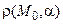от точки M₀(x₀, y₀, z₀) до плоскости 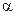, заданной уравнением (4.5), вычисляется по формуле

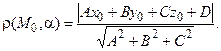
Пример 4.8. Cоставить уравнение плоскости, проходящей через точки М₁(1, 0, –1), М₂(2, –3, 0), М₃(4, 7, 1).

Решение. Воспользуемся формулой (4.6):

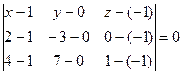или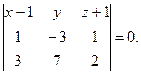

Раскрыв определитель, получаем искомое уравнение плоскости:

13x – y – 16z – 29 = 0.

Линии второго порядка

Линией второго порядка называется множество точек плоскости, координаты x, y которых в прямоугольной системе координат удовлетворяют уравнению второй степени

Ax² + Bxy + Cy² + Dx + Ey + F = 0. (4.7)

Уравнение (4.7) называется общим уравнением линии второго порядка (А, В, С не равны нулю одновременно).

При помощи преобразования прямоугольной системы координат (параллельного переноса и поворота) всегда можно найти такую новую прямоугольную систему координат, в которой уравнение (4.7) имеет один из следующих трех видов (каноническое уравнение):

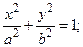(4.8)

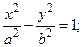(4.9)

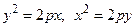, (4.10)

где a, b, p – положительные числа. Уравнение (4.7) может определять так называемую вырожденную кривую (пустое множество, точ-ку, прямую, пару прямых). При этом линия, приводимая к виду (4.8), (4.9), (4.10), называется соответственно эллипсом, гиперболой или параболой.

Эллипс с каноническим уравнением 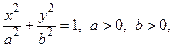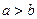, имеет форму, изображенную на рис. 4.4.

Рис. 4.4

Точки F₂(–с, 0) и F₁(с, 0), где 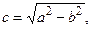называются фокусами эллипса.

Числа а и b называются полуосями эллипса.

Гипербола с каноническим уравнением 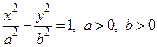имеет форму, изображенную на рис. 4.5.

Рис. 4.5

Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А₁(а,0), А₂(–а, 0), называемых вершинами гиперболы. Числа a и b – полуоси гиперболы: а – действительная полуось, b – мнимая. Точки F₂(–c, 0) и F₁(c, 0), где 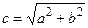, называются фокусами гиперболы.

Парабола с каноническим уравнением 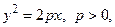имеет форму, изображенную на рис. 4.6.

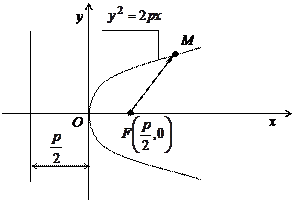
Рис. 4.6

Число p называется параметром параболы, точка О – ее вершиной, а ось Оx – осью параболы, вектор 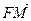– фокальный радиус-вектор точки М. Прямая 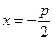называется директрисой параболы.

Пример 4.9. Упростить уравнение пользуясь переносом начала координат. Построить линию, определяемую этим уравнением.

Решение. Выделим полные квадраты по переменным x и y соответственно.

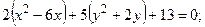
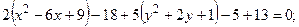
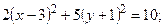
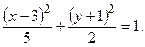
Обозначая х – 3 = X, y + 1 = Y, получим каноническое уравнение эллипса 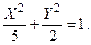Начало новой системы координат – точка О₁(3, –1); оси ОX, ОY параллельны осям Оx и Оy соответственно. Большая полуось эллипса 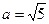, малая полуось 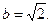Изобразим кривую на рис. 4.7.

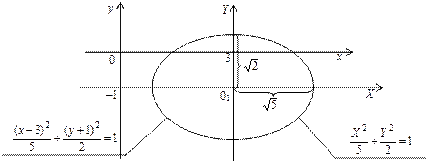
Рис. 4.7