Примеры. 1.Найти частные производные функции:
1.Найти частные производные функции:
а) 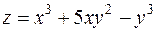 .
.
Считая 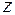 функцией одной переменной – аргумента
функцией одной переменной – аргумента 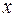 , находим
, находим
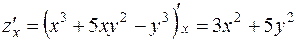 ;
;
аналогично для случая, если 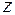 функция одной переменной – аргумента
функция одной переменной – аргумента 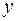 :
:
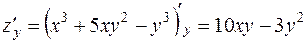
б) 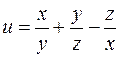 .
.
Считая 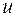 функцией одной переменной – только аргумента
функцией одной переменной – только аргумента 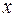 , затем только
, затем только 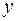 и далее только
и далее только 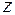 , находим
, находим
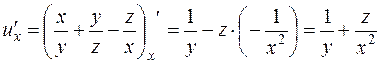 ;
;
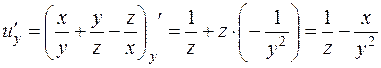 ;
;
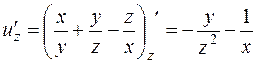 .
.
в) 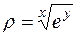 .
.
Перепишем функцию в виде 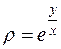 и найдем частные производные, полагая
и найдем частные производные, полагая
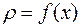 и
и 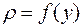 .
.
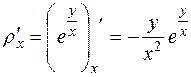 и
и 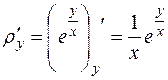 .
.
2.Вычислить значения частных производных функции при указанных значениях аргументов:
а) 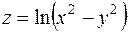 ;
; 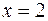 ,
, 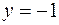 .
.
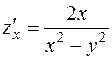 ;
; 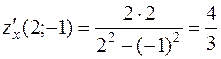
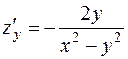 ;
; 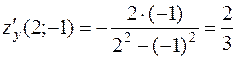 .
.
3.Проверить, что данная функция 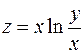 удовлетворяет уравнению
удовлетворяет уравнению 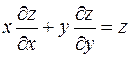 .
.
Преобразуем функцию и найдем ее частные производные.
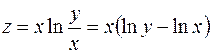
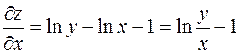 ;
; 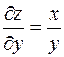
Подставим найденные частные производные и функцию в преобразованном виде в исходное уравнение:
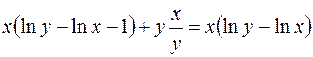
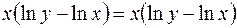
Тождество доказано. Это означает, что данная функция удовлетворяет указанному уравнению (является его решением).
5. Дифференциалы ФНП. Геометрический смысл полного дифференциала
1°. Частным дифференциалом по х функции 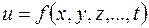 называется главная часть соответствующего частного приращения
называется главная часть соответствующего частного приращения 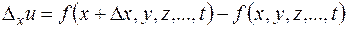 , линейная относительно приращения Dх (или, что то же, дифференциала
, линейная относительно приращения Dх (или, что то же, дифференциала 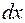 ).
).
Аналогично определяются частные дифференциалы функции по каждому из остальных аргументов. Обозначаются, соответственно, 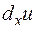 ,
, 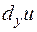 ,
, 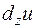 …
…
Из определения частных производных следует
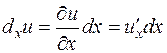 ,
,  ,
, 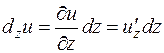 …
…
2°. Для функции 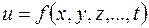 выражение
выражение
 (1)
(1)
называется полным приращением.
Если функция f(x, y) имеет непрерывные частные производные, то
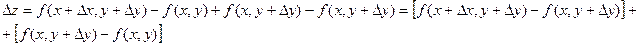 Применим теорему Лагранжа к выражениям, стоящим в квадратных скобках.
Применим теорему Лагранжа к выражениям, стоящим в квадратных скобках.

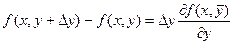
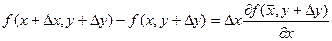
здесь 
Тогда получаем
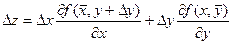
Т.к. частные производные непрерывны, то можно записать равенства:
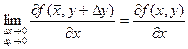
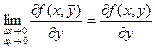
Если функция определена в окрестности точки 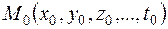 и имеет непрерывные частные производные в этой точке, то полное приращение можно выразить в виде
и имеет непрерывные частные производные в этой точке, то полное приращение можно выразить в виде
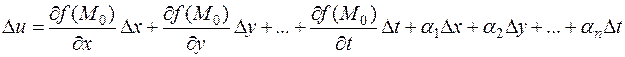 или
или
 ,
,
где a1…an – бесконечно малые функции при Dх®0, Dу®0 … Dt®0 соответственно;
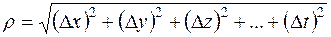 ;
; 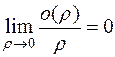 .
.
3°. Полным дифференциаломфункции 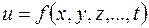 называется главная часть ее полного приращения (1), линейная относительно приращений ее аргументов
называется главная часть ее полного приращения (1), линейная относительно приращений ее аргументов 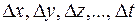 (или, что то же, дифференциалов
(или, что то же, дифференциалов  ).
).
Полный дифференциалфункции 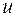 , если он существует, равен сумме всех ее частных дифференциалов
, если он существует, равен сумме всех ее частных дифференциалов
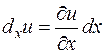
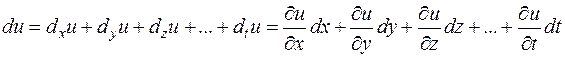
4°. Функция 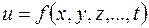 называется дифференцируемой в точке, если в этой точке она имеет полный дифференциал. Если функция дифференцируема в каждой точке области, то она называется дифференцируемой в этой области.
называется дифференцируемой в точке, если в этой точке она имеет полный дифференциал. Если функция дифференцируема в каждой точке области, то она называется дифференцируемой в этой области.
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
