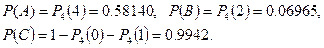Формула полной вероятности.

Формулы Байеса.

Одним из эффективных методов подсчёта вероятностей является формула полной вероятности, с помощью которой решается широкий круг задач.

Пусть событие A может наступить с одним и только одним из нескольких попарно несовместных событий Н₁, Н₂,…,Н_n, называемых гипотезами, т.е.

.

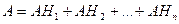Так как Н₁, Н₂,…Н_n попарно несовместны, то несовместны и события АН₁, АН₂,…АН_n . Отсюда получаем, применяя формулы сложения и умножения вероятностей

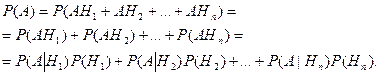
Полученная формула

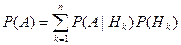(1)

называется формулой полной вероятности.

Пример 1. (см. пример 1 §8). Из урны, в которой находятся m белых и n-m чёрных шаров, без возвращения выбираются два шара. Найдём вероятность события B={второй вынутый шар – белый},

Рассмотрим гипотезы: H₁= {первый вынутый шар – белый) и 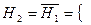первый вынутый шар – чёрный}. Тогда 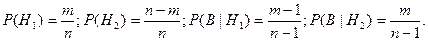По формуле полной вероятности получаем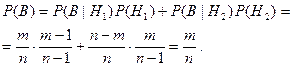

Таким образом, мы получим

.

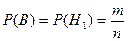Аналогично можно установить, что вынимая последовательно без возвращения шары, мы получим одну и ту же вероятность вынуть белый шар на любом месте. Таким образом, при правильно организованной жеребьёвке, шансы всех участников одинаковы, независимо от того, в какой очерёдности они тянут жребий.

Замечание. Эту же задачу можно интерпретировать, как вычисление вероятности вытащить белый шар из урны, из которой был случайно утерян один или несколько шаров.

В тесной связи с формулой полной вероятности находятся так называемые формулы Байеса. Они относятся к той же ситуации, что и формула полной вероятности.

Поскольку событие А может наступить только вместе с одним из n попарно несовместных событий Н₁,…Н_{n ,} то найдём вероятность Р(Н_к | А) – вероятность того, что событие А наступит вместе с гипотезой Н_к.

По формуле умножения получаем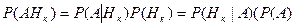

Откуда имеем

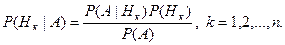(2)

Или, если воспользоваться формулой полной вероятности (1) получим:

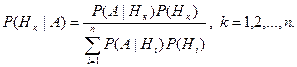(3)

Это и есть формулы Байеса.

Запомнить эти формулы нетрудно: в знаменателе стоит выражение для полной вероятности, а в числителе – одно из слагаемых (к-ое) в этом выражении.

Формулы Байеса можно интерпретировать следующим образом.

Пусть A – результат некоторого эксперимента,

Н_к – гипотезы. Вероятности Р(Н_к) – это априорные вероятности гипотез, вычисленные до проведения опыта, а условные вероятности Р(Н_к|А) – это апостериорные вероятности гипотез, вычисляемые после того, как стал известен исход эксперимента А. Формулы Байеса позволяют по априорным вероятностям гипотез и по условным вероятностям события А при гипотезах 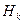вычислять апостериорные вероятности Р(Н_к|А).

Пример 2. При обследовании больного имеется подозрение на одно из двух заболеваний Н₁ и Н₂. Их вероятности в данных условиях Р(Н₁ )=0,6, Р(Н₂ )=0,4. Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезни Н₁ вероятность положительной реакции равна 0,9, отрицательной – 0,1. В случае Н₂ положительная и отрицательная реакции равновероятны. Анализ провели дважды, и оба раза реакция оказалась отрицательной (событие А). Требуется найти вероятности каждого заболевания после проделанных анализов.

Решение. В случае заболевания Н₁ событие А происходит с вероятностью 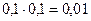, а в случае заболевания Н₂ – с вероятностью 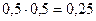. Следовательно по формуле Байеса имеем .

.

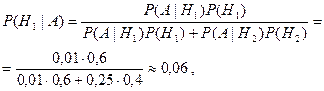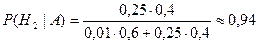Отсюда видно, что полученные результаты анализов дают веские основания предполагать болезнь Н₂.

Комбинаторика.

Решение вероятностных задач на классическую схему часто облегчается использованием комбинаторных формул. Каждая из комбинаторных формул определяет общее число элементарных исходов 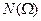в некотором опыте, состоящем в выборе наудачу m элементов из n различных элементов исходного множества M={x₁,x₂,…,x_n}. При этом в постановке каждого такого опыта строго оговорено, каким образом производится выбор и что понимается под различными выборками.

Существуют две принципиально различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов (без повторения). Это значит, что отбираются либо сразу все m элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества. Во второй схеме (с повторениями) выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательным перемешиванием исходного множества перед следующим выбором.

После того, как выбор тем или иным способом осуществлен, отобранные элементы (или их номера) могут быть либо упорядочены (т.е. выложены в последовательную цепочку), либо нет. В результате получаются следующие четыре различные постановки эксперименты по выбору наудачу m элементов из общего числа n различных элементов множества М.

1. Схема выбора, приводящая к размещениям. Опыт состоит в выборе m элементов без возвращения, но с упорядочиванием их по мере выбора в последовательную цепочку. Различными исходами данного опыта будут упорядоченные m-элементные подмножества множества М, отличающиеся либо набором элементов, либо порядком их следования. Получаемые при этом комбинации элементов (элементарные исходы) называются размещением без повторений из n элементов по m, а их общее число определяется формулой

.

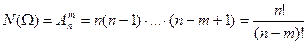В частном случае, когда 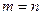, т.е. в выборке (строке) участвуют все элементы множества М (причём каждый по одному разу), опыт фактически состоит в произвольном упорядочивании множества М, т.е. сводится к случайной перестановке элементов всего множества. При этом, получаем, что (число различных перестановок из n элементов) в этом случае

.

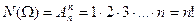Замечание. Примем по определению равенство 0!=1.

2. Схема выбора, приводящая к размещениям с повторениями. Выбор m элементов из множества М={x₁,x₂,…,x_n} производится с возвращением и с упорядочиванием. Различными исходами будут всевозможные m-элементные наборы (вообще говоря, с повторениями), отличающиеся либо составом элементов, либо порядком их следования. Например при m =4 множества (строк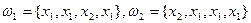и) и 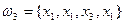считаются различными исходами данного опыта. Полученные в результате комбинации называются размещением с повторениями из n элементов по m. Их общее число определяется формулой

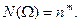
Пример 1. 7 одинаковых шариков случайным образом рассыпают по 4 лункам (в одну лунку может поместиться любое число шариков). Сколько существует различных способов распределения 7 шариков по 4 лункам? Какова вероятность того, что в результате данного опыта первая лунка окажется пустой (при этом может оказаться пустой и еще какая-либо лунка)?

Решение. Занумеруем лунки и шарики. Можно считать, что опыт состоит в 7-кратном выборе с возвращением номера лунки. Строка (х₁,х₂,…,х₇) полностью характеризует распределение шариков по лункам (х_i – номер лунки в которую попал i-ый шар). Каждое из чисел х₁,х₂,…,х₇может принимать любое целое значение (номер лунки) от 1 до 4. Так, например, строка (1,1,3,1,4,4,2) означает, что в первую лунку попали шары с номерами 1,2,4, во вторую лунку – шар №7, в третью – шар №3, в четвертую – шары №5 и №6. Таким образом, число всех распределений 7 шариков по 4 лункам равно числу различных строк длиной 7 из множества M={1,2,3,4}. Следовательно, их будет .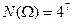

Событие А={первая лунка окажется пустой} соответствует такому выбору, когда номер 1 (номер первой лунки) удалён из строки. Поэтому 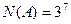и значит .

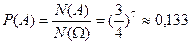Пример 2. Множество М состоит из 10 первых букв русского алфавита. Опыт состоит в выборе без возвращения 4 букв и записи слова в порядке поступления букв. Сколько 4-буквенных слов может быть получено в данном опыте? Какова вероятность того, что наудачу составленное слово будет оканчиваться буквой «а» (событие А)?

Решение. 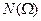– число всех 4-буквенных слов в данном опыте – равно числу 4-элементных упорядоченных подмножеств множества из 10 букв, т.е. .

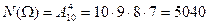Событию А соответствует число способов разместить на 3 оставшихся места по одной букве из 9 (буква «а» исключена из рассмотрения, поскольку её место уже определено). Таким образом 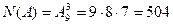и значит .

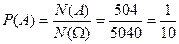3. Схема выбора, приводящего к сочетаниям без повторения. Опыт состоит в выборе m элементов без возвращения и без упорядочивания. Различными исходами следует считать m – элементные подмножества множества М, имеющие различный состав. Получаемые при этом комбинации элементов (элементарные исходы) носят название сочетания из n элементов по m, а их общее число 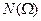определяется по формуле

.

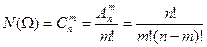Числа 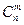называются биномиальными коэффициентами.

Для них справедливы следующие тождества, полезные при решении задач:

1. 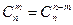(свойство симметрии)

2. 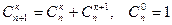(рекуррентное соотношение)

3. Имеет место следующая формула, называемая формулой бинома Ньютона

.

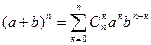Пример 3 (задача о выборке). Из партии, содержащей n изделий, среди которых n₁ бракованных, наудачу извлекают m изделий для контроля. Найти вероятность следующего события А={в полученной выборке содержится ровно m₁ бракованных изделий}.

Решение. Занумеруем изделия числами от 1 до n. Согласно описанию эксперимента производится выбор без возвращения и без упорядочивания m элементов из n. Поэтому число таких выборок равна 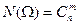. Cобытию А благоприятствуют такие исходы когда m₁ элемент выборки из m изделий принадлежит множеству из 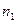бракованных изделий, а остальные m-m₁ изделие этой выборки принадлежит множеству из m- 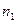не бракованных изделий. Число всех таких исходов равно 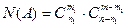(поскольку на каждую выборку m₁ бракованных изделий из 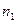бракованных приходится 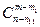выборок m-m₁ не бракованных изделий из общего числа n- 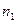не бракованных). Окончательно получаем

.

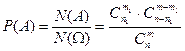4. Схема выбора, приводящая к сочетаниям с повторениями. Опыт состоит в выборе с возвращением m элементов множества М={ x₁,x₂,…,x_n }, но без последующего упорядочивания, то есть различными исходами такого опыта будут всевозможные m -элементные наборы, отличающиеся составом. Например, при m =4 наборы 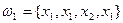и 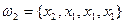неразличимы для данного эксперимента, а набор 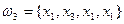отличен от любого из предыдущих. Получающиеся в результате данного опыта комбинации называются сочетаниями с повторениями, а их общее число определяется формулой

.

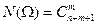Замечание. Эта схема в задачах на классическую схему теории вероятностей используется редко, поскольку исходы по этой схеме выбора часто оказываются не равноправными.

5. Размещения данного состава. Полиномиальная формула.Пусть 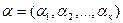– строка длиной к, составленная из элементов упорядоченного множества X={a₁,а₂,…,а_n}, состоящего из n-элементов. Тогда каждому номеру i из совокупности 1,2,…, n будет соответствовать число к_i, показывающее, сколько раз элемент а_i встречается в строке 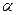. Выписывая по порядку эти числа, получаем новую строку (к₁, к ₂,…, к _n), которую называют составомстроки 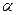. Например, если X={а₁,а₂,а₃,а₄} и 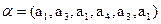, то строка имеет состав (3,0,2,1) (в ней элемент а₁ встречается 3 раза, элемент а₂ – 0 раз, а₃ – 2 раза, а₄ – 1 раз). Две строки, имеющие один и тот же состав, могут отличаться друг от друга лишь порядком номеров. Их называют размещениями (с повторениями) данного состава. Число размещений имеющий данный состав ( к₁, к₂,…, к_n ) будет выражаться следующей формулой

.

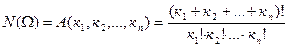Аналогично формуле Бинома Ньютона, имеет место полиномиальная формула

,

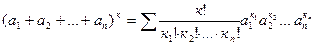где суммирование в правой части формулы производится по всевозможным наборам целых неотрицательных чисел к₁,к₂,…,к_n таких, что к₁+к₂+…+к_n=к.

Пример 4. Игральную кость бросают 10 раз. Какова вероятность, что при этом грани 1,2,3,4,5,6 выпадут соответственно 2,3,1,1,1,2 раза (событие А),

Решение. Число всех строк длиной 10 из элементов множества X ={1,2,3,4,5,6} равно 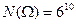. благоприятными для А будут строки, в которых элементы 1,2,3,4,5,6 встречаются соответственно 2,3,1,1,1,2 раза, т.е. строки, имеющие состав (2,3,1,1,1,2). Число таких строк будет равно:

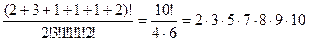
Отсюда искомая вероятность будет равна .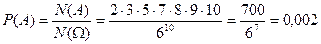

В заключение этого параграфа приведём пример, являющийся обобщением задачи о выборке.

Пример 5. В урне имеется n шаров; из них: n₁ шаров 1-го цвета,…, n_i шаров i-го цвета,…, 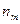шаров m-го цвета (n₁+n₂+…+n_m=n). Из урны вынимается одновременно к шаров. Найти вероятность того, что среди них будет: к₁ шаров 1-го цвета,…, к_m шаров m-го цвета, где к₁+к₂+…+к_m=к (событие А).

Решение. Общее число случаев равно числу способов, какими можно вынуть к шаров из n, т.е. 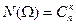. Число благоприятных событию А случаев будет равно

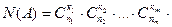
Так как группу шаров первого цвета можно выбрать 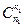способами, группу шаров второго цвета 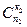способами и т.д. Искомая вероятность будет равна

.

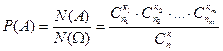Схема Бернулли

Опыты называются независимыми, если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты.

Замечание. Независимые опыты могут производиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого-то события А во всех опытах одна и та же, во втором случае она меняется от опыта к опыту.

Пусть теперь производится n независимых опытов, в каждом из которых с одной и той же вероятностью p может наступить некоторое событие А. Требуется найти вероятность Р_n(к) того, что в n опытах событие А наступит ровно к раз (событие В).

Описанная схема называется схемой независимых испытаний, или схемой Бернулли, по имени швейцарского математика конца XVII и начала XVIII века Якоба Бернулли, изучавшего её.

Найдем вероятность Р_n(к). Событие В можно представить в виде суммы ряда элементарных событий – вариантов события А. Каждый вариант события А можно записать в виде строки длиной n (число опытов), в которой к компонент соответствуют событию А, а остальные n-к компонент событию 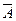. Например, один из возможных вариантов есть

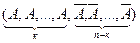
(успех и 1,2,…,k-м опытах и неудача в остальных).

Число всех вариантов равно 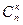(числу сочетаний из n элементов по к), а вероятность каждого варианта в виду независимости опытов равна р^кq^n-к ( где q=1-р ). Отсюда вероятность события В будет равна

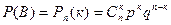. (1)

Формула (1) носит название формулы Бернулли.

Отсюда следует, что вероятность, хотя бы одного появления события А при n независимых испытаниях (опытах) в одинаковых условиях равна

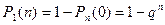(2)

Пример 1. Монета бросается 5 раз. Какова вероятность того, что герб выпадет при этом 3 раза?

Решение. В данном случае событием А считается выпадение герба, вероятность p этого события в каждом опыте равна 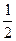. Отсюда

P= .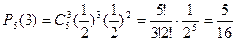

Для наглядности условимся каждое наступление события А рассматривать как успех. Если зафиксировать n, то, Р_n(к). есть функция аргумента к, принимающая значения 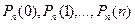. Выясним, при каком значении к функция Р_n(к) принимает наибольшее значение, т.е., какое число успехов к₀ является наиболее вероятным при данном числе опытов n. Оказывается что число к=к₀ можно определить из двойного неравенства.

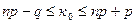(3)

Разность граничных значений в этом двойном неравенстве равна 1. Если np+p не является целым числом, то двойное неравенство определяет лишь одно наивероятнейшее значение к₀.Если же np+p – целое число, то имеются два наивероятнейших значения: 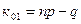и .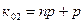

Пример 2. Игральную кость бросают 20 раз. Каково наиболее вероятное число выпадений грани «6» ?

Решение. В данном случае n = 20, 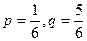откуда 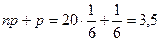. Поскольку nр + р не целое число, то наибольшим среди чисел Р₂₀(0), Р₂₀(1),…, Р₂₀(20) будет число Р₂₀(3). Следовательно, наиболее вероятное число выпадений грани «6» будет 3. Найдём, чему равна вероятность такого числа выпадений. По формуле Бернулли имеет:

.

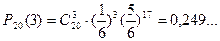Из формулы (3) видно, что одно из двух ближайших к nр целых чисел является наиболее вероятным числом успехов.

Оказывается, число nр допускает и другую интерпретацию. А именно: nр можно рассматривать, в определенном смысле, как среднее число успехов в n опытах. Будем исходить из частотного истолкования вероятности. Назовем (для краткости) n- кратное повторение данного опыта серией. Пусть мы произвели N серий. Пусть в первой серии было получено к₁ успехов, во второй – к₂ , ….., в N-ой –к_N. Составим среднее арифметическое этих чисел

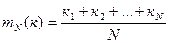. (4)

Равенство (4) - есть среднее число успехов в N сериях. Оказывается, что с увеличением N указанное среднее арифметическое приближается к некоторому постоянному значению, а именно к числу np.

Действительно запишем (4) в виде:

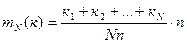. (5)

Поскольку каждая серия состоит из n опытов, то производя N серий мы осуществляем данный опыт 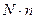раз.

Написанная дробь (5) со знаменателем Nn есть нечто иное как отношение общего числа успехов в этих 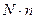опытах к числу всех опытов. С увеличением N (а значит, и Nn ) эта дробь будет приближаться к числу р- вероятности успеха. Следовательно, число (4) будет приближаться к рn, что и требовалось получить.

Пример 3. Станок штампует изделия. Вероятность р брака одного изделия равна 0,05. Чему равно среднее число бракованных изделий на сотню?

Решение. Искомое число бракованных изделий равно: .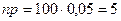

Замечание 1. Можно рассмотреть более общую схему независимых испытаний. Рассмотрим n независимых испытаний (в различных условиях), причём вероятность события А («успеха») в i-ом опыте равна p_i, a q_i=1-p_i – вероятность неуспеха в i-м испытании ( i=1,2,…,n ). Тогда можно показать, что вероятность P_n(к) того, что событие А появится в этих n опытах ровна к раз, равна коэффициенту при z^k в разложении по степеням z функции

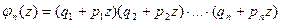. (6)

Такую схему независимых испытаний называют схемой Пуассона. Схема Пуассона при p_i=p превращается в схему Бернулли. Вероятности P_n(к) в схеме Пуассона не записываются в компактном виде аналогичной формуле(1). Из (6) , например, следует:

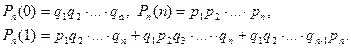
Замечание 2. Схемы Бернулли и Пуассона допускают обобщение на тот случай, когда в результате каждого опыта возможные не два исхода (А или 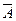), а несколько исходов.

Если производится n независимых опытов (схема Бернулли) причём каждый опыт может иметь к исключающих друг друга исходов 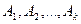, с вероятностями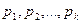 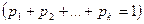, то вероятность того, что в m₁ опытах появится событие А₁, в m₂ опытах событие А₂ и т.д., в m_k опытах событие А_к 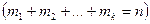выражается формулой

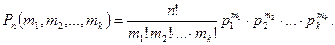(7)

Если условия опыта различны (схема Пуассона), т.е.

в i-омопыте событие A_j имеет вероятность p_ji (i=1,2,…,n; j=1,2,…,k), то вероятность 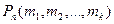вычисляется как коэффициент при члене 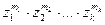в разложении по степеням 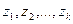функции:

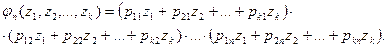(8)

Пример 4. Завод изготавливает изделия, каждое из которых подвергается четырём видам испытаний. Первое испытание изделия проходит благополучно с вероятностью 0,9; второе с вероятностью 0,95; третье-0,8 и четвертое-0,85. Найти вероятность того, что изделие пройдет благополучно:

A- все четыре испытания

B- ровно два испытания (из четырех)

C- не менее двух испытании (из четырех)

Решение. В условиях задачи проводятся четыре независимых опыта (испытания) в различных условиях. Вероятность события. А – испытание прошло благополучно, в каждом опыте разное. Искомые вероятности находим из формулы (6)

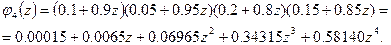
Отсюда получаем: