Модуль 7. Теорія ймовірностей.
Контрольна робота № 6 виконується учнями після вивчення наступних розділів програми:
· Основні означення, поняття і теореми теорія ймовірностей випадкових подій.
· Класична ймовірність.
· Основні теореми теорії ймовірностей.
· Формула повної ймовірності, формула Байєса.
Завдання . Розв’язати задачу.
1. З 15 надрукованих книг три виявилися з браком. Яка ймовірність того, що дві вибрані навмання книжки будуть без браку ?
Розв’язування.
► Нехай подія А полягає в тому, що дві вибрані навмання книги будуть без браку. З 15 книг вибрати дві можна 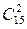 способами ( число комбінацій із 15 по 2 ). Усі ці події є рівноможливими і попарно несумісними. Отже, загальна кількість рівноможливих результатів дорівнює
способами ( число комбінацій із 15 по 2 ). Усі ці події є рівноможливими і попарно несумісними. Отже, загальна кількість рівноможливих результатів дорівнює 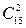 . Сприятливою подією для події А є вибір двох небракованих книг із 12 небракованих ( 15 – 3=12 ). Отже, число сприятливих результатів (подій) для події А дорівнює
. Сприятливою подією для події А є вибір двох небракованих книг із 12 небракованих ( 15 – 3=12 ). Отже, число сприятливих результатів (подій) для події А дорівнює 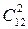 . Звідси, за формулою класичної ймовірності, одержуємо:
. Звідси, за формулою класичної ймовірності, одержуємо:
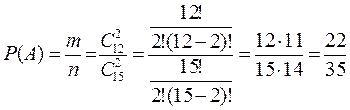 . ◄
. ◄
2. Група туристів, у якій шість юнаків і чотири дівчини, вибирає жеребкуванням чотирьох чергових. Яка ймовірність того, що буде вибрано два юнака і дві дівчини ?
Розв’язування.
► Число результатів (елементарних подій) під час вибирання чотирьох
чергових із 10 туристів дорівнює  . Усі ці події є рівноможливі і попарно несумісні.
. Усі ці події є рівноможливі і попарно несумісні.
Нехай подія А полягає в тому, що серед чотирьох чергових є два юнаки і дві дівчини. Вибрати двох юнаків із шести можна 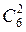 способами, а вибрати двох дівчат із чотирьох можна
способами, а вибрати двох дівчат із чотирьох можна 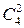 способами. За правилом добутку вибір і двох юнаків, і двох дівчат можна виконати
способами. За правилом добутку вибір і двох юнаків, і двох дівчат можна виконати 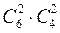 способами – це і кількість подій для події А. Тоді, за формулою класичної ймовірності. Маємо
способами – це і кількість подій для події А. Тоді, за формулою класичної ймовірності. Маємо
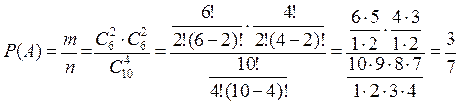 . ◄
. ◄
3. Два баскетболісти кидають незалежно один від одного м’яч в корзину. Імовірність попадання для першого спортсмена дорівнює 0,75, а для другого – 0,8. Визначити імовірність попадання м’яча в корзину.
Розв’язування.
► Нехай А – попадання в корзину першого баскетболіста, В – попадання другого, С – попадання в корзину.
Подію С можна подати у вигляді суми трьох відповідних подій:
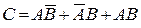 , де
, де 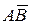 – подія, яка полягає в тому, що перший баскетболіст попаде в корзину, а другий ні,
– подія, яка полягає в тому, що перший баскетболіст попаде в корзину, а другий ні, 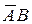 – подія, яка полягає в тому, що другий баскетболіст попаде в корзину, а перший ні,
– подія, яка полягає в тому, що другий баскетболіст попаде в корзину, а перший ні, 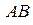 – обидва попали в корзину.
– обидва попали в корзину.
Кожен із доданків суми є добутком двох незалежних подій, а тому для обчислення їх імовірності можна застосувати теорему множення, а для обчислення імовірності події С – теорему додавання:

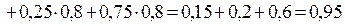 , де
, де 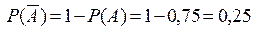 ,
, 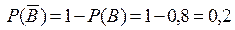 . ◄
. ◄
4. Три стрілка незалежно один від одного стріляють в ціль. Ймовірність попадання в ціль для першого стрілка дорівнює 0,7, для другого – 0,85, для третього – 0,9. Визначити ймовірність того, що в ціль попаде принаймні один стрілок.
Розв’язування.
► Обчислимо ймовірності протилежних подій 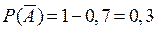 ( ймовірність промаху першого стрілка);
( ймовірність промаху першого стрілка); 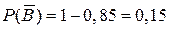 ( ймовірність промаху другого стрілка);
( ймовірність промаху другого стрілка); 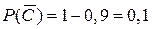 ( ймовірність промаху третього стрілка); тоді
( ймовірність промаху третього стрілка); тоді 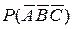 – ймовірність одночасного промаху всіх трьох стрілків – обчислюється за теоремою про добуток:
– ймовірність одночасного промаху всіх трьох стрілків – обчислюється за теоремою про добуток:
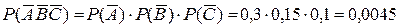
Але подія, протилежна події 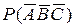 , полягає в попаданні в ціль принаймні одного стрілка. Отже, шукана ймовірність
, полягає в попаданні в ціль принаймні одного стрілка. Отже, шукана ймовірність 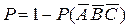 , тобто
, тобто 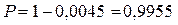 . ◄
. ◄
5. В коробці знаходяться 20 зелених і 5 червоних кульки. Послідовно дістають 6 кульок, причому кожну обрану кульку повертають назад в коробку перед вийманням наступної. Яка ймовірність того, що серед вибраних кульок 4 зелені кульки?
Розв’язування.
► Ймовірність витягнути зелену кульку 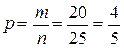 можна вважати однією й тією в усіх шести випробуваннях;
можна вважати однією й тією в усіх шести випробуваннях; 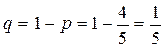 – ймовірність витягнути червону (не зелену) кульку. Використовуючи формулу Бернуллі, маємо
– ймовірність витягнути червону (не зелену) кульку. Використовуючи формулу Бернуллі, маємо
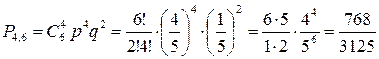 . ◄
. ◄
6. Маємо дві одинакові на вигляд урни. В першій урні 15 білих і 5 чорних кульок, в другій – 10 білих та 10 чорних кульок. З навмання вибраної урни дістали кульку. Обчислити ймовірність того, що ця кулька біла.
Розв’язування.
► Нехай 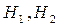 – гіпотези, що полягають в виборі відповідно першої та другої урни. Вибір будь-якої урни рівноможливий, тому
– гіпотези, що полягають в виборі відповідно першої та другої урни. Вибір будь-якої урни рівноможливий, тому 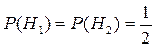 . Подія А – поява білої кульки , тоді
. Подія А – поява білої кульки , тоді 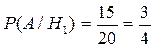 – ймовірність витягнути білу кульку з першої урни,
– ймовірність витягнути білу кульку з першої урни, 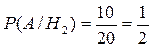 – ймовірність витягнути білу кульку з другої урни. Шукану ймовірність знаходимо за формулою повної ймовірності:
– ймовірність витягнути білу кульку з другої урни. Шукану ймовірність знаходимо за формулою повної ймовірності:
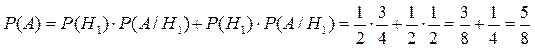 . ◄
. ◄
Завдання для контрольних робіт
Контрольна робота № 1.
Модуль 1. «Комплексні числа».
Модуль 2. «Лінійна алгебра».
Теми: «Комплексні числа і дії над ними», «Форми запису комплексних чисел», «Елементи теорії матриць», «Загальна теорія СЛАР». 
Завдання 1. Для комплексних чисел 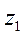 та
та 
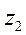 :
:
а) знайти модуль та головне значення;
б) записати їх в тригонометричній та показникові формах;
в) обчислити суму, різницю, добуток та частку комплексних
чисел 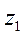 та
та 
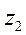 .
.
1. 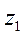
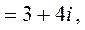
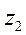
 .
.
2. 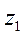
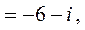
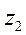
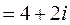 .
.
3. 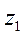
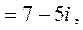
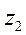
 .
.
4. 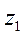
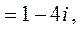
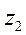
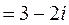 .
.
5. 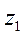
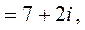
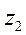
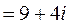 .
.
6. 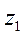
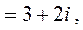
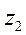
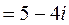 .
.
Завдання 2. Розв’язати рівняння:
1. 
2. 
3. 
4. 
5. 
6. 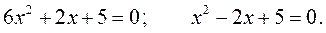
Завдання 3. Піднести до степеня:
1. 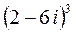 ;
; 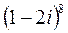 ; 4.
; 4. 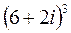 ;
; 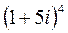 ;
;
2. 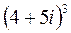 ;
; 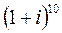 ; 5.
; 5. 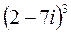 ;
; 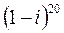 ;
;
3. 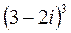 ;
; 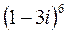 ; 6.
; 6. 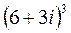 ;
; 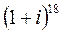 .
.
Завдання 4. Обчислити визначники матриць:
1. а) 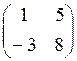 б)
б) 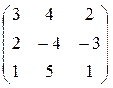
2. а) 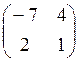 б)
б) 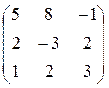
3. а) 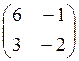 б)
б) 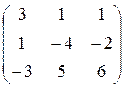
4. а) 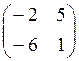 б)
б) 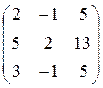
5. а) 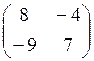 б)
б) 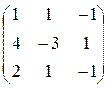
6. а) 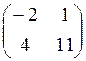 б)
б) 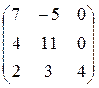
Завдання 5. Розв’язати систему лінійних рівнянь методом Крамера:
1. 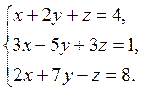 2.
2. 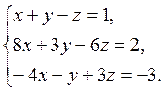
3. 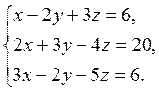 4.
4. 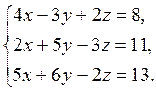
5. 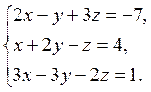 6.
6. 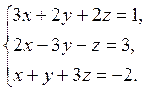
Контрольна робота № 2.

Модуль 3. «Аналітична геометрія на площині».
Теми: «Лінії на площині», «Криві другого порядку».
Завдання 1. Відомі вершини трикутника АВС. Знайти:
а) рівняння сторони АВ;
б) кут В трикутника АВС.
Виконати рисунок.
1. А(8, 6), В(6, 4), С(-2, 14).
2. А(4, 6), В(2, 2), С(-1, 3).
3. А(-6, -2), В(-3, 1), С(1, -4).
4. А(-1, -1), В(1, 3), С(5, -2).
5. А(-8, 4), В(-2, 1), С(1, -3).
6. А(2, -5), В(1, -3), С(4, 1).
Завдання 2. Привести задане рівняння еліпса до канонічного вигляду і обчислити його осі. Виконати рисунок.
1. 4х2+9у2=36; 4. 16х2+4у2=64;
2. 25х2+4у2=100; 5. 4х2+36у2=144;
3. 9х2+25у2=225; 6. 49х2+9у2=441;
Завдання 3. Обчислити координати фокусів і ексцентриситет заданої гіперболи. Виконати рисунок.
1. 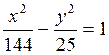 4.
4. 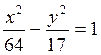
2. 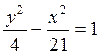 5.
5. 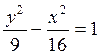
3. 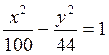 6.
6. 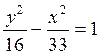
Завдання 5. Знайти фокус і директрису для заданої параболи. Виконати рисунок.
1. 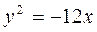 4.
4. 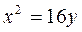
2. 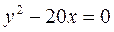 5.
5. 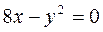
3. 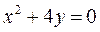 6.
6. 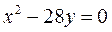
Контрольна робота № 3.

Модуль 4. «Диференціальне числення функцій».
Теми: «Диференційованість функції однієї змінної», «Основні теореми диференціального числення», «Схема дослідження функції і побудова її графіка», «Диференційованість функцій багатьох змінних», «Дослідження функцій багатьох змінних на екстремум, умовний екстремум».
Завдання 1. Знайти похідні функцій: а) складної функції; б) неявної функції; в) параметрично заданої функції; г) використовуючи логарифмічне диференціювання.
1. а) 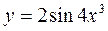 ; б)
; б)  ;
;
в) 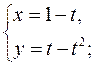 г)
г)  .
.
2. а) 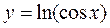 ; б)
; б) 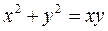 ;
;
в) 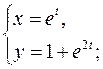 г)
г)  .
.
3. а) 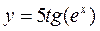 ; б)
; б) 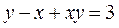 ; в)
; в) 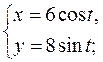 г)
г) 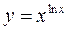 .
.
4. а) 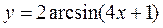 ; б)
; б) 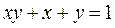 ;
;
в) 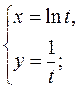 г)
г) 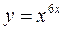 .
.
5. а) 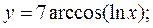 б)
б) 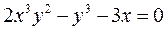 ;
;
в) 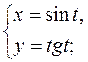 г)
г) 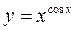 .
.
6. а) 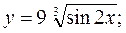 б)
б) 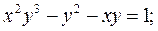
в) 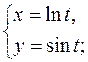 г)
г) 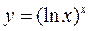 .
.
Завдання 2. Знайти найбільше та найменше значення функції на заданому проміжку :
1) 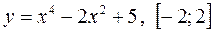 ; 4)
; 4) 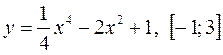 ;
;
2) 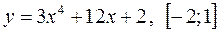 ; 5)
; 5) 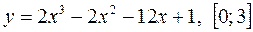 ;
;
3) 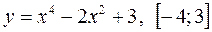 ; 6)
; 6) 
Завдання 3. Знайти всі похідні другого порядку для заданих функцій:
1. 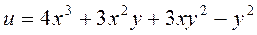 ;
;
2. 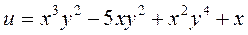 ;
;
3. 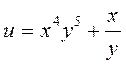 ;
;
4. 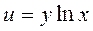 ;
;
5. 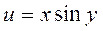 ;
;
6. 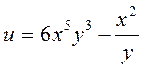 .
.
Завдання № 4. Довести, що задана функція  z задовольняє задане
z задовольняє задане
рівняння:
1. 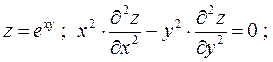
2. 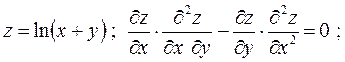
3. 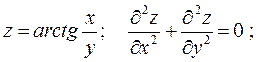
4. 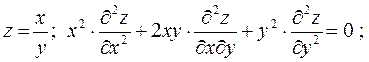
5. 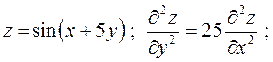
6. 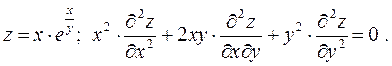
Завдання № 5. Дослідити задану функцію на екстремум.
1. 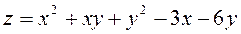 ;
;
2. 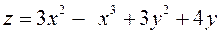 ;
;
3. 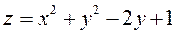 ;
;
4. 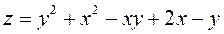 ;
;
5. 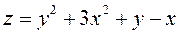 ;
;
6. 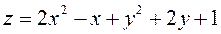 .
.
Контрольна робота № 4.
Модуль 5. «Інтегральне числення функцій».
Теми: «Невизначений інтеграл», «Визначений інтеграл», «Застосування визначених інтегралів».
Завдання 1. Знайти невизначені інтеграли. Результат перевірити диференціюванням:
1. а) 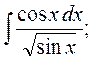 б)
б) 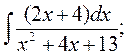
2. а) 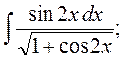 б)
б) 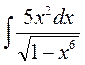 ;
;
3. а) 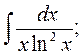 б)
б) 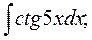
4. а) 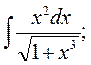 б)
б) 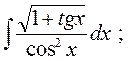
5. а) 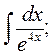
 б)
б) 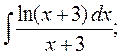 6. а)
6. а) 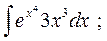 б)
б) 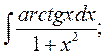
Завдання 2. Обчислити визначені інтеграли:
1. а) 
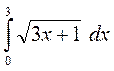 ; б)
; б) 
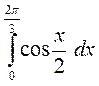 ; 2. а)
; 2. а) 
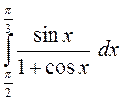 ; б)
; б) 
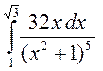 ; 3. а)
; 3. а) 
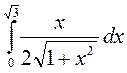 ; б)
; б) 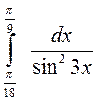 ; 4. а)
; 4. а) 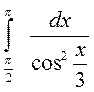 ; б)
; б)  ;
;
5. а) 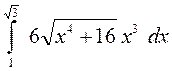 ; б)
; б) 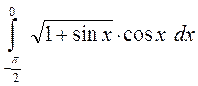 ;
;
6. а) 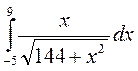 ; б)
; б) 
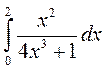 ;
;
Завдання 3 . Обчислити площу фігури, обмеженої графіками функцій:
1. 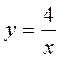 ;
; 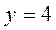 ;
; 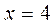 ;
;
2. 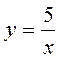 ;
; 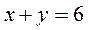 ;
;
3. 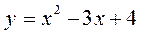 ;
; 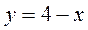 ;
;
4. 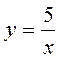 ;
; 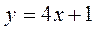 ;
; 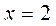 ;
;
5. 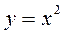 ;
; 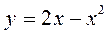 ;
;
6. 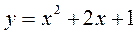 ;
; 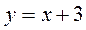 .
.
Контрольна робота № 5.
Модуль 6. «Диференціальні рівняння ».
Теми: «Диференціальні рівняння 1-го порядку», «Диференціальні рівняння 2-го порядку, що дозволяють знизити порядок», «Лінійні диференціальні рівняння 2-го порядку».
Завдання 1. Знайти загальний розв’язок (інтеграл) диференціальних рівнянь першого порядку:
1. 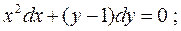 2.
2. 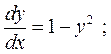
3. 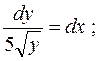 4.
4. 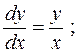
5. 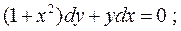 6.
6. 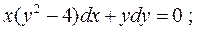
Завдання 2. Знайти загальний розв’язок (інтеграл) диференціальних рівнянь другого порядку:
1.  ; 2.
; 2. 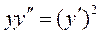 ;
;
3. 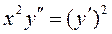 ; 4.
; 4.  ;
;
5. 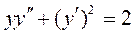 ; 6.
; 6. 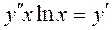 .
.
Завдання 3. Знайти загальний розв’язок (інтеграл) лінійних диференціальних рівнянь другого порядку:
1. 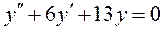 ; 2.
; 2. 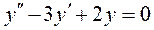 ;
;
3. 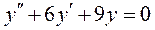 ; 4.
; 4. 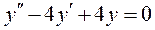 ;
;
5. 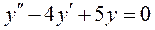 ; 6.
; 6. 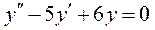 .
.
Контрольна робота № 6.
Модуль 7. «Теорія ймовірностей».
Теми: «Основні означення, поняття і теореми теорія ймовірностей випадкових подій», «Класична ймовірність. Основні теореми теорії ймовірностей. Формула повної ймовірності, формула Байєса».
Завдання 1. Розв’язати задачу.
1. У коробці містяться 7 білих і 5 чорних кульки. З коробки виймають навмання 6 кульок. Знайти ймовірність події: А – усі кульки білі; С – чотири білі та дві чорні.
2. У лотереї 100 білетів із них 30 – виграшні. Яка ймовірність того, що з придбаних трьох білетів тільки один виграшний ?
3. Із 14 учнів, серед яких 5 дівчат, на вечір зустрічі без вибору запрошують трьох учнів. Яка імовірність, що серед запрошених буде одна дівчина?
4. В групі 13 хлопців та 12 дівчат. На кожне з трьох питань, заданих вчителем, відповіли по одному учню. Яка ймовірність того, що серед учнів, що відповідали було два хлопці і одна дівчина?
5. Кожен з трьох робітників виготовив по 15 деталей. Під час перевірки виявилося, що серед деталей виготовлених першим, другим і третім робітником окремо, стандартних деталей було 12, 10 і 11 відповідно. У кожного робітника взяли навмання по дві деталі. Яка ймовірність того, що всі шість взяті деталі будуть стандартними ?
6. Із двох гармат стріляють по цілі. Імовірність влучення у ціль першою і другою гарматою відповідно дорівнюють 0,6 і 0,9.Знайти ймовірність того, що при одному залпі по цілі влучать тільки з однієї гармати ?
Завдання 2. Розв’язати задачу.
1. Монету підкидають 8 раз. Яка ймовірність, того що 6 раз вона упаде
гербом вверх ?
2. Три спортсмени намагаються влучити в ціль незалежно один від
одного. Ймовірність влучення відповідно дорівнюють 0,3; 0,1; 0,6.
Знайти ймовірність того, що: а) хоча б один спортсмен влучив у ціль;
б) два спортсмени влучили в ціль.
3. Імовірність того, що замовлення в бібліотеці першої книги буде
виконане, дорівнює 0,5, другої – 0,7, третьої – 0,4. Визначити
ймовірність того, що бібліотека виконає замовлення: а) принаймні
на одну книгу; б) рівно на дві книги.
4. В наслідок багаторічних спостережень помітили, що з 1000
новонароджених у середньому 515 хлопчиків і 485 дівчаток. Знайти
ймовірність того, що в родині, де п’ятеро дітей, не більш як три
хлопчики?
5. Троє студентів розв’язують одну задачу. Яка імовірність того, що
задача буде розв’язана, якщо ймовірність зробити це для них дорівнює
р1 = 0,5; р2 = 0,7; р3 = 0,45 ?
6. У першому ящику міститься 5 білих кульок, 11чорних та 8 зелених, а
в другому – 10 білих, 8 чорних і 6 зелених. Навмання беруть по одній
кульці з кожного ящика. Яка ймовірність того, що вони одного
кольору?
Завдання 3. Розв’язати задачу.
1. У рибалки є три улюблених місця риболовлі, які він відвідує з
однаковою ймовірністю. Ймовірність клювання на І місці – 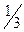 ;
;
на ІІ – 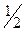 ; на ІІІ –
; на ІІІ – 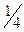 . Рибалка закинув вудку у навмання вибраному
. Рибалка закинув вудку у навмання вибраному
місці. Знайти ймовірність того, що: а) риба клюнула; б) риба клюнула
на І місці .
2. У комп’ютерному магазині за рік продано 1000 моніторів, 300
принтерів 100 сканерів. Протягом гарантійного терміну в сервісний центр надходять на ремонт у середньому 0,5  моніторів, 1
моніторів, 1  принтерів
принтерів
і 1,5  сканерів. Знайти ймовірність того, що навмання вибрана з перерахованих за серійним номером одиниця товару надійшла протягом гарантійного терміну на ремонт у сервісний центр є монітор.
сканерів. Знайти ймовірність того, що навмання вибрана з перерахованих за серійним номером одиниця товару надійшла протягом гарантійного терміну на ремонт у сервісний центр є монітор.
3. На заводі металевих виробів болти виготовляють на трьох машинах.
Перша машина виробляю 25  , друга – 35
, друга – 35  і третя – 40
і третя – 40  усієї
усієї
продукції, а брак становить відповідно 3  , 5
, 5  і 2
і 2  . а) Яка ймовірність
. а) Яка ймовірність
того, що навмання взятий болт виявиться бракованим ? б) Навмання
взятий болт виявився бракованим. Яка ймовірність того, що він
зроблений третьою машиною ?
4. Маємо три одинакові на вигляд урни. В першій урні 25 білих кульок, в
другій – 10 білих та 15 чорних кульок, третій – 25 чорних кульок. З
навмання вибраної урни дістали білу кульку. Обчислити ймовірність
того, що кульку дістали з другої урни.
5. У цеху 20 верстатів. З них 10 марки А, 6 марки В і 4 марки С.
ймовірність того, що якість деталі виявиться найвищою, для цих
верстатів відповідно становить 0,9; 0,8; 0,7. 1) Знайти, який відсоток
деталей вищої якості випускає цех в цілому ? 2) Якість деталі, взятої
навмання, виявилася найвищою. Яка ймовірність того, що вона
зроблена на верстаті марки А?
6. В першій урні 7 синіх та 8 зелених кульок, в другій 5 синіх та 6 зелених
кульок. З другої урни в першу поклали одну кульку, а потім з першої
навмання дістали одну кульку. Знайти ймовірність того, що вийнята
кулька – синя.
