Теорема Гаусса для вектора . Поток вектора сквозь произвольную замкнутую поверхность равен минус избыточному связанному заряду диэлектрика внутри этой поверхности
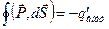 . (82)
. (82)
Доказательство. Пусть замкнутая поверхность S охватывает часть диэлектрика (заштрихован на рис.25, слева). При включении поля вследствие поляризации заряд проходит через элемент dS этой поверхности (на рис.26 справа – увеличенный фрагмент). Пусть смещение положительного заряда характеризуется вектором 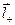 , а отрицательного – вектором
, а отрицательного – вектором 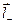 . Через dS наружу выйдет положительный заряд
. Через dS наружу выйдет положительный заряд 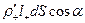 из внутренней (пунктирной) части косого цилиндра, а внутрь войдет отрицательный заряд
из внутренней (пунктирной) части косого цилиндра, а внутрь войдет отрицательный заряд 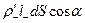 из внешней части цилиндра, что эквивалентно переносу положительного заряда в обратном направлении. Значит, суммарный связанный заряд, выходящий наружу через dS, равен
из внешней части цилиндра, что эквивалентно переносу положительного заряда в обратном направлении. Значит, суммарный связанный заряд, выходящий наружу через dS, равен
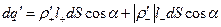 =
= 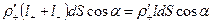 ,
,
где 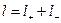 - расстояние, на которое сместились друг относительно друга центры масс положительных и отрицательных зарядов при поляризации. Согласно (80)
- расстояние, на которое сместились друг относительно друга центры масс положительных и отрицательных зарядов при поляризации. Согласно (80) 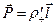 , Þ
, Þ 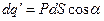 =
= 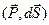 . Проинтегрировав это выражение, найдем весь заряд, который вышел из объема внутри замкнутой поверхности S при поляризации. Внутри останется избыточный заряд -
. Проинтегрировав это выражение, найдем весь заряд, который вышел из объема внутри замкнутой поверхности S при поляризации. Внутри останется избыточный заряд -  противоположного знака, Þ получим выражение (82):
противоположного знака, Þ получим выражение (82): 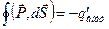 , что и требовалось доказать.
, что и требовалось доказать.
Теорема Гаусса для поля вектора 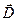 . Поскольку источниками электрического поля являются любые заряды, а именно: связанные и сторонние (т.е. не входящие в состав молекул диэлектрика, мы их обозначали просто q), то теорему Гаусса для вектора
. Поскольку источниками электрического поля являются любые заряды, а именно: связанные и сторонние (т.е. не входящие в состав молекул диэлектрика, мы их обозначали просто q), то теорему Гаусса для вектора  можно переписать так
можно переписать так 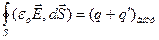 . Подставим
. Подставим  из (74):
из (74): 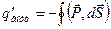 , Þ
, Þ 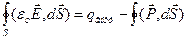 . Учитывая, что оба интеграла берутся по одной поверхности S, перенесем второй интеграл влево и запишем под одним знаком:
. Учитывая, что оба интеграла берутся по одной поверхности S, перенесем второй интеграл влево и запишем под одним знаком: 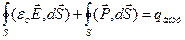 , Þ
, Þ 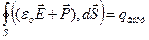 . Вспомогательный вектор во внутренних круглых скобках обозначают
. Вспомогательный вектор во внутренних круглых скобках обозначают
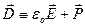 . (83)
. (83)
и называют электрическим смещением. Тогда для него можно компактно сформулировать теорему Гаусса:
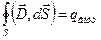 . (84)
. (84)
Поток вектора 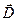 сквозь любую замкнутую поверхность равен суммарному стороннему заряду внутри этой поверхности.
сквозь любую замкнутую поверхность равен суммарному стороннему заряду внутри этой поверхности.
Связь между векторами  и
и 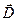 . Подставив выражение (81), верное только для изотропных диэлектриков:
. Подставив выражение (81), верное только для изотропных диэлектриков: 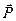 =æεо
=æεо  ® (83), получим
® (83), получим 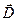 =εо(1+æ)
=εо(1+æ)  , или
, или
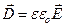 , (85)
, (85)
где диэлектрическая проницаемость ε=æ+1. Для всех веществ 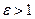 , а для вакуума
, а для вакуума 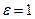 . Из (85) следует, что векторы
. Из (85) следует, что векторы  и
и 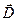 направлены одинаково. Поскольку источниками вектора
направлены одинаково. Поскольку источниками вектора 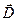 являются только сторонние заряды, линии вектора
являются только сторонние заряды, линии вектора 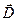 проходят области с диэлектриком, не прерываясь. Это позволяет выбрать правильную тактику при решении задач: сначала найти вектор
проходят области с диэлектриком, не прерываясь. Это позволяет выбрать правильную тактику при решении задач: сначала найти вектор 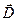 , а затем, используя (85), вычислить вектор
, а затем, используя (85), вычислить вектор  (ибо расположение сторонних зарядов обычно известно, а распределение связанного заряда представляет весьма сложную задачу).
(ибо расположение сторонних зарядов обычно известно, а распределение связанного заряда представляет весьма сложную задачу).
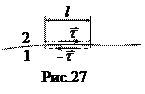 Условия для векторов
Условия для векторов  и
и 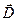 на границе раздела диэлектриков. Пусть два однородных изотропных диэлектрика имеют общую границу (рис.27), и напряженность электрического поля в диэлектрике 1 равно
на границе раздела диэлектриков. Пусть два однородных изотропных диэлектрика имеют общую границу (рис.27), и напряженность электрического поля в диэлектрике 1 равно 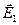 , а в диэлектрике 2 -
, а в диэлектрике 2 - 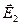 . Возьмем вдоль границы прямоугольный контур столь малой длины l, чтобы вдоль него напряженность
. Возьмем вдоль границы прямоугольный контур столь малой длины l, чтобы вдоль него напряженность  в каждом диэлектрике пренебрежимо мало изменялась. Устремим высоту контура к нулю, тогда циркуляция вдоль этого контура сведется к сумме вдоль сторон l и по теореме о циркуляции должна быть равна нулю:
в каждом диэлектрике пренебрежимо мало изменялась. Устремим высоту контура к нулю, тогда циркуляция вдоль этого контура сведется к сумме вдоль сторон l и по теореме о циркуляции должна быть равна нулю:
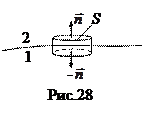
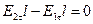 , Þ
, Þ 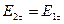 . Это значит: тангенциальная составляющая вектора
. Это значит: тангенциальная составляющая вектора  одинакова по обе стороны от границы.
одинакова по обе стороны от границы.
Теперь возьмем цилиндр малого сечения S на границе раздела (рис.28). Тогда по теореме Гаусса для вектора 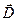 (при стремлении высоты цилиндра к нулю и одновременно к границе):
(при стремлении высоты цилиндра к нулю и одновременно к границе): 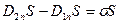 , где s - поверхностная плотность стороннего заряда на границе раздела. Отсюда
, где s - поверхностная плотность стороннего заряда на границе раздела. Отсюда 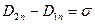 . Если сторонних зарядов на границе раздела нет, то
. Если сторонних зарядов на границе раздела нет, то 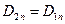 , т.е. нормальная составляющая вектора
, т.е. нормальная составляющая вектора 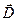 одинакова по обе стороны от границы.
одинакова по обе стороны от границы.
Величины 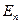 и
и 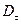 меняются при переходе границы. Запишем (85) в проекциях:
меняются при переходе границы. Запишем (85) в проекциях: 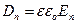 , Þ
, Þ 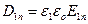 ,
, 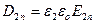 , и так как
, и так как 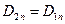 , Þ
, Þ 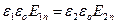 , Þ
, Þ 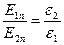 . Это значит, нормальная составляющая вектора
. Это значит, нормальная составляющая вектора  терпит скачок при переходе границы, а сами линии вектора
терпит скачок при переходе границы, а сами линии вектора  преломляются. Запишем (85) в проекции на тангенциальное направление:
преломляются. Запишем (85) в проекции на тангенциальное направление: 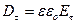 , Þ
, Þ  ,
, 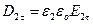 , и так как
, и так как 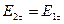 , Þ
, Þ 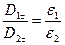 . Это значит, тангенциальная составляющая вектора
. Это значит, тангенциальная составляющая вектора 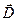 терпит скачок при переходе границы, а сами линии вектора
терпит скачок при переходе границы, а сами линии вектора 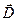 преломляются. Сопоставление выражений в рамках показывает, что если
преломляются. Сопоставление выражений в рамках показывает, что если 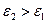 , то при переходе из среды 1 в среду 2 нормальная компонента вектора
, то при переходе из среды 1 в среду 2 нормальная компонента вектора  уменьшается, а тангенциальная компонента вектора
уменьшается, а тангенциальная компонента вектора 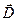 увеличивается.
увеличивается.
 Энергия электрического поля. Рассмотрим процесс зарядки конденсатора (рис.29). Пусть верхняя пластина заряжена зарядом +q до потенциала φ1, а нижняя – зарядом -q до потенциала φ2. Работа против сил поля при переносе очередной порции заряда +dq>0 с нижней пластины на верхнюю идет на увеличение энергии взаимодействия зарядов:
Энергия электрического поля. Рассмотрим процесс зарядки конденсатора (рис.29). Пусть верхняя пластина заряжена зарядом +q до потенциала φ1, а нижняя – зарядом -q до потенциала φ2. Работа против сил поля при переносе очередной порции заряда +dq>0 с нижней пластины на верхнюю идет на увеличение энергии взаимодействия зарядов: 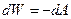 =
= 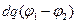 =
=  . Выразим напряжение через емкость конденсатора (
. Выразим напряжение через емкость конденсатора ( 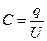 ):
): 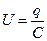 , Þ
, Þ 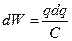 . Далее интегрируем:
. Далее интегрируем: 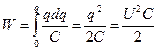 . Емкость плоского конденсатора
. Емкость плоского конденсатора 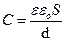 , где S – площадь каждой из пластин, d – расстояние между ними, Þ
, где S – площадь каждой из пластин, d – расстояние между ними, Þ 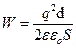 . Умножим числитель и знаменатель на S и учтем, что
. Умножим числитель и знаменатель на S и учтем, что 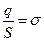 и
и  (объем пространства между пластинами), Þ
(объем пространства между пластинами), Þ 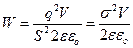 . Теперь умножим числитель и знаменатель на
. Теперь умножим числитель и знаменатель на 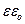 и учтем, что
и учтем, что 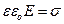 , Þ энергия заряженного конденсатора
, Þ энергия заряженного конденсатора
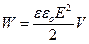 . (86)
. (86)
Отношение 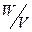 является энергией единицы объема и называется плотностью энергии электрического поля
является энергией единицы объема и называется плотностью энергии электрического поля
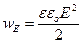 . (87)
. (87)
Учтем, что 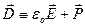 =
= 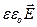 , Þ
, Þ 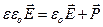 . Умножим это равенство скалярно на вектор
. Умножим это равенство скалярно на вектор  , Þ
, Þ 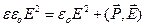 ® (87), Þ
® (87), Þ
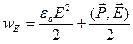 . (88)
. (88)
Полученное выражение представляет собой сумму плотности электрической энергии в вакууме и плотности энергии поляризации диэлектрика. Следовательно, электрическая энергия локализована в самом поле: как там, где есть вещество, так и там, где его нет. Однако стационарное поле может существовать только в присутствие порождающих его зарядов, а вот переменные поля могут существовать и самостоятельно.
