Теоремы о производной суммы, разности, произведения и частного двух функций одной переменной.
Производная суммы:
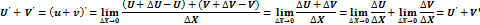
Производная произведения:
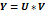
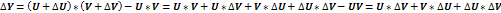
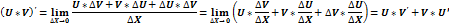
Производная частного:
Доказательство.
Формулу производной частного можно получить, следуя обычной схеме вычисления производной. Но можно поступить проще. Пусть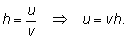 
Найдем производную функции u по правилу дифференцирования произведения: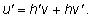 
Выразим из этой формулы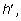 
а вместо h подставим его значение 
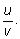Получим: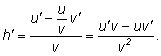 
Производная сложной функции.
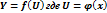
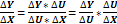
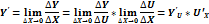
Производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
Производная обратной функции.
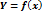
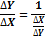
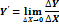
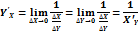
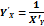
Производные функций, заданных неявно и параметрически.
Производная функции, заданной неявно;
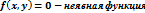
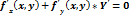
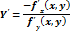
Дифференцируемость и дифференциал функции. Геометрический смысл дифференциала.
Дифференциалом функции с геометрической точки зрения является приращение ординаты касательной.
С математической точки зрения дифференциал – это главная линейная часть приращения функции.
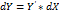, где dY – дифференциал функции, а dX – дифференциал независимой переменной.
Функция называется дифференцируемой в точке, если она имеет производную в этой точке.
Функция дифференцируема на интервале если она дифференцируема в каждой точке этого интервала.
Применение дифференциала к приближенным вычислениям.
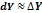
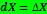
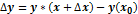
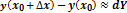
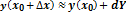
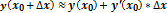
10. Основные теоремы дифференциального исчисления: теоремы Ролля, Лагранжа, Коши.
Геометрический смысл теоремы Лагранжа? Доказательство?
Теорема Ролля:
Пусть функция y=f(x):
1. Определена и непрерывна на [a,b]
2. Дифференцируема в (a,b)
3. На концах отрезка принимает равные значения.
Тогда внутри интервала найдется хотя бы одна точка С, в которой производная =0
Теорема Лагранжа;
Пусть функция y=f(x):
1. Определена и непрерывна на [a,b]
2. Дифференцируема в (a,b)
Тогда внутри (a,b) найдется хотя бы одна точка С, в которой выполняется условие:
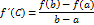
Доказательство:
Для доказательства возьмем вспомогательную функцию: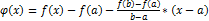 
Эта функция удовлетворяет всем трем условиям теоремы Ролля.
1. 
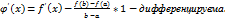
2. 
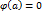
3. 
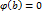
Тогда существует точка С, такая что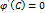 
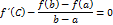
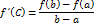
Ч.Т.Д.
Теорема Коши:
Пусть функция f(x) и g(x):
1. Определена и непрерывна на [a,b]
2. Дифференцируема в (a,b)
3. 
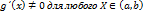
Тогда внутри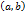 
найдется хотя бы одна точка С, в которой выполняется условие
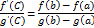
Доказательство:
Для доказательства возьмем вспомогательную функцию: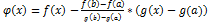 
. Эта функция удовлетворяет всем 3 условиям теоремы Ролля:
1. Определена и непрерывна на отрезке [a,b]
2. 
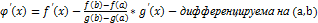
3. 
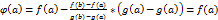
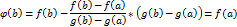
Тогда найдется точка С,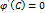
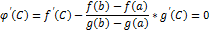
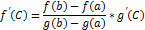
Тогда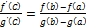 
Ч.Т.Д.
Правило Лопиталя.
1)Правило Лопиталя:
Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки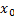 
, за исключением, быть может, самой этой точки; 
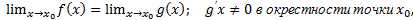за исключением, быть может, самой этой точки; существует конечный предел 
.
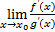Тогда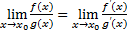 
2) Правило Лопиталя:
Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки 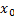, за исключением, быть может, самой этой точки; 
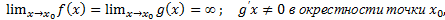за исключением, быть может, самой этой точки; существует конечный предел .
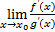Тогда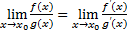
Замечания к 1 и 2:
1. Правило Лопиталя действует не всегда, т.е. предел отношения функций может существовать когда предел отношения производных не существует.
2. Если f’(x) и g’(x)=0 или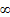 
, то правила Лопиталя можно использовать повторно.