Коэффициенты множественной корреляции и детерминации
Коэффициент множественной корреляции характеризует тесноту линейной связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.
Независимо от формы связи коэффициент множественной корреляции может быть найден следующим образом:
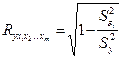 (4.12)
(4.12)
где 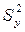 – оценка общей дисперсии результативного признака;
– оценка общей дисперсии результативного признака; 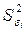 – оценка остаточной дисперсии.
– оценка остаточной дисперсии.
Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина коэффициента множественной корреляции должна быть больше или равна максимальному парному коэффициенту корреляции:
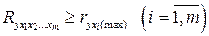 . (4.13)
. (4.13)
При правильном включении факторов в регрессионную модель величина коэффициента множественной корреляции будет существенно отличаться от коэффициента корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то коэффициент множественной корреляции может практически совпадать с коэффициентом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что сравнивая коэффициенты множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.
Расчет коэффициента множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:
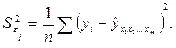 (4.14)
(4.14)
Можно пользоваться следующей формулой коэффициента множественной детерминации:
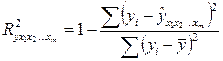 (4.15)
(4.15)
При линейной зависимости признаков формула коэффициента множественной корреляции может быть представлена следующим выражением:
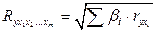 , (4.16)
, (4.16)
где 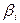 – стандартизованные коэффициенты регрессии;
– стандартизованные коэффициенты регрессии; 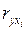 – парные коэффициенты корреляции результата с каждым фактором.
– парные коэффициенты корреляции результата с каждым фактором.
Формула коэффициента множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.
Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:
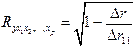 , (4.17)
, (4.17)
где
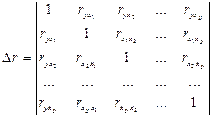 (4.18)
(4.18)
– определитель матрицы парных коэффициентов корреляции;
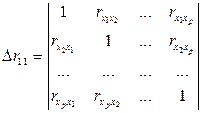 (4.19)
(4.19)
– определитель матрицы межфакторной корреляции.
Как видим, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
Скорректированный коэффициент множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов 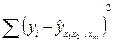 делится на число степеней свободы остаточной вариации
делится на число степеней свободы остаточной вариации 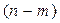 , а общая сумма квадратов отклонений
, а общая сумма квадратов отклонений 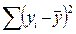 на число степеней свободы в целом по совокупности
на число степеней свободы в целом по совокупности  .
.
Формула скорректированного коэффициента множественной детерминации имеет вид:
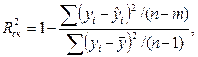 (4.20)
(4.20)
где m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.
Поскольку 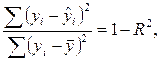 то величину скорректированного индекса детерминации можно представить в виде:
то величину скорректированного индекса детерминации можно представить в виде:
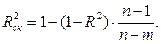 (4.21)
(4.21)
Чем больше величина m, тем сильнее различия 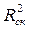 и
и 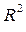 .
.
Как было показано выше, ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( 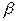 -коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции.
-коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции.
