Числові рівності, властивості істинних числових рівностей
Означення. Два числові вирази а і b, сполучені знаком «=» (дорівнює) називають числовою рівністю і позначають через а = b.
Наприклад. 2 + 5 = 7; 24 : 6 + 1 = 3.
Кожна числова рівність – це висловлення, яке може бути істинним або хибним. Числова рівність є істинною, якщо числові значення виразів,що стоять в лівій і правій частинах, рівні.
Властивості істинних числових рівностей
Відношення «дорівнює» на множині R володіє властивостями:
1) рефлективності: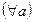 
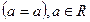
2) симетричності: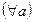 
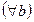
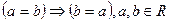
3) транзитивності: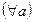 
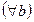
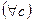
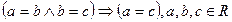
Отже, це відношення є відношенням еквівалентності.
5) монотонність множення :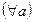 
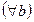
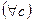
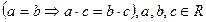
(Якщо обидві частини істинної числової рівності помножимо на один і той же числовий вираз, який має смисл, то отримаємо також істинну числову рівність).
Числові нерівності, властивості істинних числових нерівностей
Означення. Два числові вирази а і b, сполучені знаками «>» (більше) або «<» (менше) називають числовою нерівністю:
a > b або a < b – числові нерівності.
Наприклад. 45 > 23 + 12; 5 · 7 < 5 · 8; 200 < 300 – 100.
Нерівності – це також висловлення, які можуть бути істинними або хибними.
Властивості істинних числових нерівностей
Відношення «менше» на множині R володіє властивостями:
1) антисиметричності: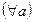 
, 
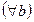
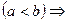
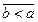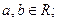
2) транзитивності: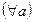 
;
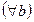
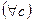
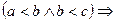
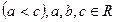3) монотонність додавання: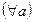 
;
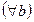
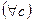
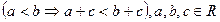(Якщо до обох частин істинної числової нерівності додати один і той же числовий вираз, який має смисл, то отримаємо також істинну числову нерівність.)
4) монотонність множення: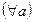 
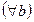
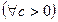
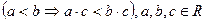
(Якщо обидві частини істинної числової нерівності помножимо на один і той же числовий вираз, який має смисл і приймає додатні значення, то отримаємо також істинну числову нерівність).
5) монотонність множення: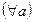 
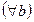
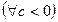
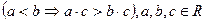
(Якщо обидві частини істинної числової нерівності помножимо на один і той же числовий вираз, який має смисл і приймає від’ємні значення, то, щоб отримати істинну числову нерівність, необхідно знак нерівності змінити на протилежний).
Рівняння та їх властивості. Нерівності, що містять змінну
План
1. Рівняння з однією змінною.
2. Рівносильність рівнянь.
3. Нерівності з однією змінною.
4. Рівносильність нерівностей.
Рівняння з однією змінною
Якщо взяти два вирази зі змінними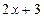 
і 
і 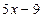з’єднати їх знаком «=», то отримаємо речення 
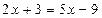. Воно містить змінну х. Якщо замість змінної х підставити певні значення, то речення перетвориться у висловлення, які можуть бути істинними або хибними. Так, якщо х = 4, то висловлення 
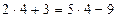істинне; якщо х = 3, то висловлення 
хибне. Тому речення 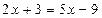є висловлювальна форма.
Означення.Нехай f (х) і g (x) – два вирази зі змінною х і областю визначення X. Тоді висловлювальна форма виду f (х) = g (x) називається рівнянням з однією змінною.
Значення змінної х із множини X, при якому рівняння перетворюється у істинну числову рівність, називається коренем або розв’язком рівняння.
Розв’язати рівняння – значить знайти множину розв’язків (коренів) рівняння.
Щоб розв’язати рівняння, його перетворюють, використовуючи теореми про рівносильність рівнянь або тотожні перетворення виразів.
Рівносильність рівнянь
Означення. Два рівняння, множини розв’язків яких на певній множині М збігаються, називаються рівносильними.
Наприклад, рівняння 
і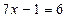 
рівносильні на множині R, бо множина коренів першого рівняння {1} і множина коренів другого рівняння{1},тобто множини коренів рівні.
Теорема 1. Нехай рівняння f (х) = g (x) задано на множині Х і h (х) – вираз, який визначений на тій же множині Х. Тоді рівняння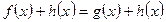 
і дане рівняння f (х) = g (x) рівносильні.
Доведення. Нехай Т1 множина розв’язків рівняння (1), а Т2 множина розв’язків рівняння (2). Покажемо, що множини коренів рівні.
Нехай число а є коренем рівняння (1). Тоді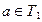 
і при підстановці у рівняння (1) обертає його у істинну числову рівність: f (а) = g (а), а вираз h (х) у числовий вираз 
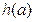. Додамо до обох частин рівності f (а) = g (а) вираз 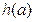. Отримаємо істинну числову рівність 
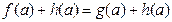, а це означає, що а є коренем рівняння (2). Отже, кожен корінь рівняння (1) є коренем рівняння (2). Аналогічно можна показати, що кожен корінь 
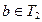рівняння (2) є коренем рівняння (1). За доведенням 
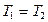і дані рівняння рівносильні.
Теорема 2. Нехай рівняння f (х) = g (x) задано на множині Х і h (х) – вираз, який визначений на тій же множині Х і який не перетворюється на нуль ні при яких значеннях х із множини Х. Тоді рівняння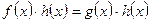 
і дане рівняння 
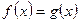рівносильні.
Доведення аналогічне до доведення першої теореми.
При розв’язуванні рівнянь частіше використовуються не самі теореми, а наслідки з них.
Наслідки з теорем про рівносильність рівнянь
До теореми 1
1. Якщо до обох частин рівняння додати одне й те саме число, то дістанемо рівняння, рівносильне даному.
2. Якщо в рівнянні перенести доданок з однієї частини в другу, змінивши його знак на протилежний, то дістанемо рівняння, рівносильне даному.
До теореми 2
3. Якщо обидві частини рівняння помножити (або поділити) на одне і те саме число, відмінне від нуля, то дістанемо рівняння, рівносильне даному.
Наприклад. Розв’язати рівняння: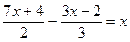 
1. Зведемо до спільного знаменника вираз у лівій частині рівняння. Це тотожне перетворення виразу. Дістанемо рівняння, рівносильне даному:
;
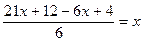2. Зведемо подібні доданки. Це тотожне перетворення виразу. Дістанемо рівняння, рівносильне даному:
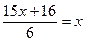
3. За наслідком (3) з теорем про рівносильність рівнянь помножимо обидві частини рівняння на 6. Дістанемо рівняння, рівносильне даному:
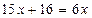
4. За наслідком (1) з теорем про рівносильність рівнянь перенесемо вираз 6х з правої частини рівняння в ліву, а число 16 – з лівої частини рівняння в праву, змінивши їх знаки на протилежні. Дістанемо рівняння, рівносильне даному:
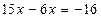
5. Зведемо подібні в лівій частині рівняння. Це тотожне перетворення, тому дістанемо рівняння, рівносильне даному:
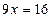
6. Поділимо ліву і праву частини рівняння на 9. За наслідком (3) дістанемо рівняння рівносильне даному.
; 
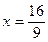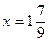
Отже, множина розв’язків рівняння складається з одного числа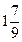 
, тобто { }.
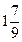В початковому курсі математики розглядаються найпростіші рівняння виду: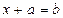 
; 
; 
; 
; 
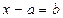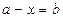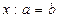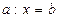, де а і b – цілі невід’ємні числа, х – змінна та рівняння на дві дії. Поняття рівняння вводиться неявно, через текст, тобто контекстуально. Розв’язуються такі рівняння в початковій школі на основі знань учнів залежностей між компонентами і результатом дій.
Наприклад. Розв’язати рівняння: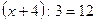 
. Невідоме знаходиться у діленому. Щоб знайти ділене, треба частку помножити на дільник. Дістанемо рівняння: 
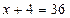. Невідомий перший доданок; щоб його знайти, треба від суми відняти другий доданок. 
; 
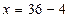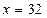. Отже, розв’язком рівняння є число 32.