Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4; 0), чем от точки В(1; 0).
Для студентов 1 курса ЗФО (кроме экономистов)
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Задание №1
Даны векторы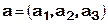 
, 
, 
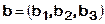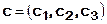и 
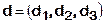в некотором базисе. Показать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе.
1. a = (1, 2, 3), b = (-1, 3, 2), c = (7, -3, 5), d = (6, 10, 17).
2. a = (4, 7, 8), b = (9, 1, 3), c = (2, -4, 3), d = (1, -13, -13).
3. a = (8, 2, 3), b = (4, 6, 10), c = (3, -2, 10), d = (7, 4, 11).
4. a = (10, 3, 1), b = (1, 4, 2), c = (3, 9, 2), d = (19, 30, 7).
5. a = (2, 4, 1), b = (1, 3, 6), c = (5, 3, 1), d = (24, 20, 6).
6. a = (1, 7, 3), b = (3, 4, 2), c = (4, 8, 9), d = (7, 32, 14).
7. а = (1, -2, 3), b = (4, 7, 2), c = (6, 4, 2), d = (14, 18, 6).
8. a = (1, 4, 3), b = (6, 8, 5), c = (3, 1, 4), d = (21, 18, 33).
9. a = (2, 7, 3), b = (3, 1, 8), c = (2, 1, 8), d = (16, 14, 27).
10. a = (7, 2, 1), b = (4, 3, 5), c = (3, 4, -2), d = (2, -5, -13).
Задание №2
Даны координаты вершин пирамиды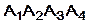 
. Найти:
1) длину ребра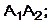 
2) угол между ребрам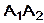и 
и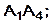 
4) угол между ребром 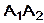и гранью 
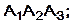5) площадь грани 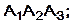6) объем пирамиды; 7) уравнение прямой 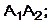8) уравнение плоскости 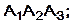9) уравнение высоты, опущенной из вершины 
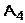на грань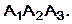 
Сделать чертеж.
1. 
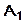(4; 2; 5), 
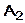(0; 7; 2), 
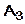(0; 2; 7), 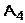(1; 5; 0).
2. 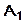(4; 4; 10), 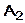(4; 10; 2), 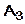(2; 8; 4), 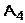(9; 6; 4).
3. 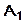(4; 6; 5), 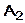(6; 9; 4), 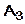(2; 10; 10), 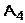(7; 5; 9).
4. 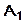(3; 5; 4), 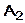(8; 7; 4), 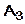(5; 10; 4), 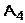(4; 7; 8).
5. 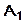(10; 6; 6), 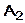(-2; 8; 2), 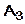(6; 8; 9), 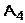(7; 10; 3).
6. 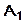(1; 8; 2), 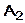(5; 2; 6), 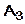(5; 7; 4), 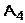(4; 10; 9).
7. 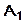(6; 6; 5), 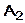(4; 9; 5), 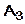(4; 6; 11), 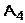(6; 9; 3).
8. 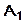(7; 2; 2), 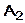(5; 7; 7), 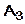(5; 3; 1), 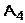(2; 3; 7).
9. 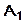(8; 6; 4), 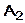(10; 5; 5), 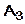(5; 6; 8), 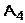(8; 10; 7).
10. 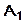(7; 7; 3), 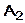(6; 5; 8), 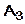(3; 5; 8), 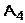(8; 4; 1).
Задание №3
1. Уравнение одной из сторон квадрата х + 3y – 5 = 0. Составить уравнения трех остальных сторон квадрата, если P(-1; 0) – точка пересечения его диагоналей. Сделать чертеж.
2. Даны уравнения одной из сторон ромба х – 3y + 10 = 0 и одной из его диагоналей х + 4y – 4 = 0; диагонали ромба пересекаются в точке Р(0; 1). Найти уравнения остальных сторон ромба. Сделать чертеж.
3. Уравнения двух сторон параллелограмма х + 2y + 2 = 0 и х + y – 4 = 0, а уравнение одной из его диагоналей x – 2 = 0. Найти координаты вершин параллелограмма. Сделать чертеж.
Даны две вершины А(-3; 3) и В(5; -1) и точка Д(4;3) пересечения высот треугольника. Составить уравнения его сторон. Сделать чертеж.
Даны вершины А(-3; -2), В(4; -1), С(1; 3) трапеции АВСД (АД II ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершин Д этой трапеции. Сделать чертеж.
6. Даны уравнения двух сторон треугольника 5х –4y + 15 = 0 и 4х + y –9 = 0.
Его медианы пересекаются в точке Р(0; 2). Составить уравнение третьей стороны треугольника. Сделать чертеж.
Даны две вершины А(2; -2) и В(3; -1) и точка Р(1; 0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.
8. Даны уравнения двух высот треугольника х + y = 4 и y = 2x и одна из его вершин А(0; 2). Составить уравнения сторон треугольника. Сделать чертеж.
9. Даны уравнения медиан треугольника x – 2y +1 = 0 и y – 1 = 0 и одна из его вершин А(1; 3). Составить уравнения его сторон. Сделать чертеж.
10. Две стороны треугольника заданы уравнениями 5x – 2y –8 = 0 и 3x – 2y – 8 = 0, а середина третьей совпадает с началом координат. СоАставить уравнение этой стороны. Сделать чертеж.
Задание №4
1.Составить уравнение и построить линию, расстояние каждой точки которой от начала координат и от точки А (5; 0) относятся как 2:1.
2.Составить уравнение и построить линию, расстояние каждой точки которой от точки А(-1; 0) вдвое меньше расстояния ее от прямой х = -4.
3.Составить уравнение и построить линию, расстояние каждой точки которой от точки А(2; 0) и прямой 5х + 8 = 0 относятся, как 5:4.
Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4; 0), чем от точки В(1; 0).
5.Составить уравнение и построить линию, расстояние каждой точки которой от точки А(2; 0) и прямой 2x + 5 = 0 относятся, как 4:5.