Тема: Динамика поступательного движения 3 страница

ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Динамика поступательного движения
Тело массой 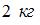движется с коэффициентом трения 0,5 по наклонной плоскости, расположенной под углом 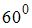к горизонту. Сила трения (в ) равна …

5 |

Решение:
На тело, движущееся по наклонной плоскости, действует сила трения

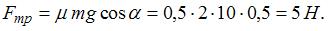
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Элементы специальной теории относительности
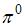-мезон, двигавшийся со скоростью 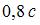(с – скорость света в вакууме) в лабораторной системе отсчета, распадается на два фотона: g₁ и g₂. В системе отсчета мезона фотон g₁ был испущен вперед, а фотон g₂ – назад относительно направления полета мезона. Скорость фотона g₁ в лабораторной системе отсчета равна …

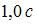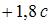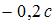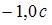Решение:
Фотон является частицей, которая может существовать, только двигаясь со скоростью с, то есть со скоростью света в вакууме. Кроме того, согласно одному из постулатов специальной теории относительности – принципу постоянства скорости света – скорость света в вакууме не зависит от движения источника света и, следовательно, одинакова во всех инерциальных системах отсчета. Поэтому скорость фотона g₁ с учетом направления его движения в лабораторной системе отсчета равна .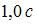

ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Работа. Энергия
Для того чтобы раскрутить стержень массы 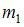и длины 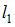(см. рисунок) вокруг вертикальной оси, проходящей перпендикулярно стержню через его середину, до угловой скорости 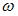, необходимо совершить работу .

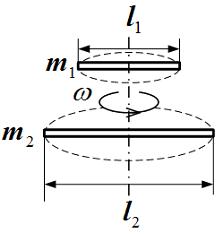
Для того чтобы раскрутить до той же угловой скорости стержень массы 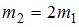и длины 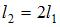, необходимо совершить работу в _____ раз(-а) бόльшую, чем .

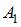8 |

Решение:
Совершенная работа равна кинетической энергии вращательного движения стержня 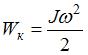, где момент инерции стержня 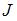пропорционален массе и квадрату длины, 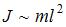(момент инерции стержня массы 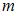и длины 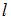относительно оси, проходящей перпендикулярно ему через середину стержня, равен 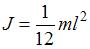). Следовательно, работа по раскручиванию до такой же угловой скорости 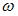стержня вдвое бόльшей массы и в два раза длиннее будет в 8 раз больше: .

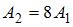ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Динамика вращательного движения
Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке:

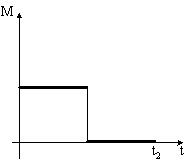
Правильно отражает зависимость момента импульса диска от времени график …

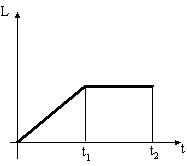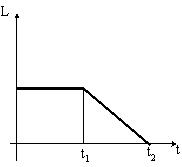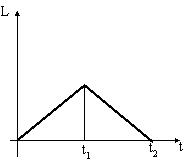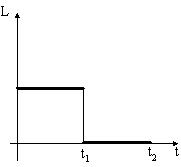Решение:
Скорость изменения величины момента импульса относительно неподвижной оси равна величине суммарного момента внешних сил относительно этой оси. 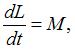где 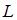– величина момента импульса, 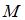– величина момента силы. Тогда величина момента импульса равна .
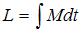Вычислив интеграл от функции, характеризующей зависимость величины момента силы от времени, получим зависимость величины момента импульса от времени.

ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Законы сохранения в механике
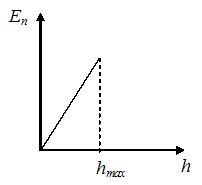
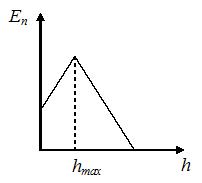
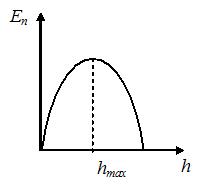
График зависимости потенциальной энергии тела, брошенного с поверхности земли под некоторым углом к горизонту, от высоты подъема имеет вид, показанный на рисунке …

ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Кинематика поступательного и вращательного движения
Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.

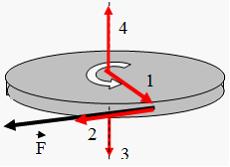
При этом правильно изображает направление углового ускорения диска вектор …

Решение:
По определению угловое ускорение тела 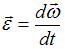, где 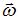– его угловая скорость. При вращении вокруг неподвижной оси векторы 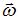и 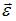коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора 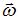связано с направлением вращения тела правилом правого винта. В данном случае вектор 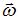ориентирован в направлении 4, а, так как после приложения силы движение становится замедленным, вектор 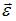ориентирован в направлении 3.

ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Динамика вращательного движения
Рассматриваются три тела: диск, тонкостенная труба и кольцо; причем массы m и радиусы R их оснований одинаковы.

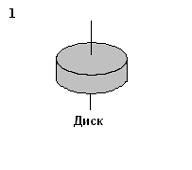
Для моментов инерции рассматриваемых тел относительно указанных осей верным является соотношение …

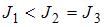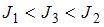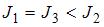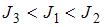Решение:
Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси вычисляется по формуле 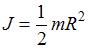, тонкостенного кругового цилиндра массы m и радиуса R относительно его оси – по формуле 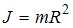. Из последней формулы видно, что момент инерции тонкостенного цилиндра (трубы, кольца) не зависит от его высоты. Поэтому правильным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение .

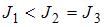ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Кинематика поступательного и вращательного движения
Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.

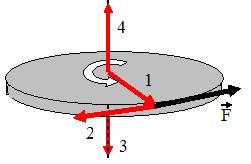
При этом правильно изображает направление углового ускорения диска вектор …

Решение:
По определению угловое ускорение тела 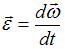, где 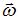– его угловая скорость. При вращении вокруг неподвижной оси векторы 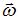и 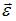коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора 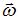связано с направлением вращения тела правилом правого винта. В данном случае вектор 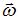ориентирован в направлении 4, и, так как после приложения силы движение становится ускоренным, вектор 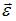ориентирован в направлении 4.

ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Элементы специальной теории относительности
Тело начало двигаться со скоростью, при которой его масса возросла на 30%. При этом длина тела в направлении движения …

			уменьшилась в 1,3 раза
			увеличилась в 1,3 раза
			уменьшилась на 30%
			увеличилась на 30%

Решение:
Зависимости релятивистской массы и линейных размеров тела в направлении движения тела от его скорости определяются по формулам: 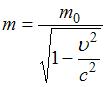(1), 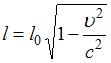(2). Из формулы (1) 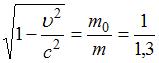. Тогда 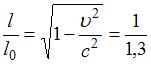, откуда следует, что длина уменьшилась в 1,3 раза.

ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Законы сохранения в механике
Диск и обруч, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми скоростями на горку. Если трением и сопротивлением воздуха можно пренебречь, то отношение высот 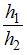, на которые смогут подняться эти тела, равно …

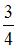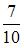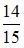Решение:
В рассматриваемой системе «тело – Земля» действуют только консервативные силы, поэтому в ней выполняется закон сохранения механической энергии, согласно которому 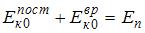, или 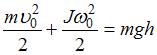, где J – момент инерции тела относительно оси, проходящей через центр масс, 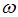– угловая скорость вращения вокруг этой оси, h – высота, на которую сможет подняться тело. Отсюда с учетом того, что 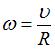, получаем: 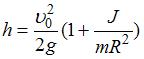. Моменты инерции диска (сплошного цилиндра) и обруча (полого цилиндра) равны соответственно 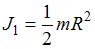и . Тогда искомое отношение высот .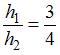

ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Динамика поступательного движения
Тело массой 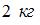движется с коэффициентом трения 0,5 по наклонной плоскости, расположенной под углом 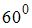к горизонту. Сила трения (в ) равна …

5

ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Работа. Энергия
Потенциальная энергия частицы задается функцией 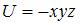. 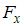-компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна …
(Функция 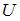и координаты точки А заданы в единицах СИ.)

6 |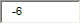

Решение:
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид 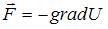, или 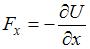, , 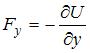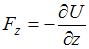. Таким образом,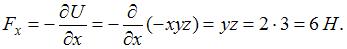

ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Динамика поступательного движения
Тело массой 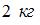движется с коэффициентом трения 0,5 по наклонной плоскости, расположенной под углом 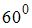к горизонту. Сила трения (в ) равна …

5

ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Работа. Энергия
Для того чтобы раскрутить стержень массы 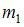и длины 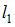(см. рисунок) вокруг вертикальной оси, проходящей перпендикулярно стержню через его середину, до угловой скорости 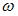, необходимо совершить работу .

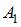Для того чтобы раскрутить до той же угловой скорости стержень массы 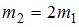и длины 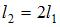, необходимо совершить работу в _____ раз(-а) бόльшую, чем .

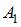8 |

Решение:
Совершенная работа равна кинетической энергии вращательного движения стержня 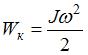, где момент инерции стержня 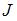пропорционален массе и квадрату длины, 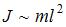(момент инерции стержня массы 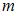и длины 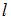относительно оси, проходящей перпендикулярно ему через середину стержня, равен 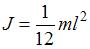). Следовательно, работа по раскручиванию до такой же угловой скорости 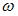стержня вдвое бόльшей массы и в два раза длиннее будет в 8 раз больше: .

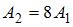ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Законы сохранения в механике
Фигурист вращается вокруг вертикальной оси с определенной частотой. Если он прижмет руки к груди, уменьшив тем самым свой момент инерции относительно оси вращения в 2 раза, то …

			частота вращения фигуриста и его кинетическая энергия вращения возрастут в 2 раза
			частота вращения фигуриста возрастет в 2 раза, а его кинетическая энергия вращения – в 4 раза
			частота вращения фигуриста уменьшится в 2 раза, а его кинетическая энергия вращения – в 4 раза
			частота вращения фигуриста и его кинетическая энергия вращения уменьшатся в 2 раза

Решение:
Согласно закону сохранения момента импульса 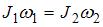. Здесь J – момент инерции фигуриста относительно оси вращения, 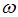– угловая скорость его вращения вокруг этой оси. Отсюда с учетом того, что 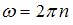, где n – частота вращения, 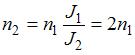. Кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна: 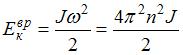. Тогда . Таким образом, частота вращения фигуриста и его кинетическая энергия возрастут в 2 раза.