Дифференциальное уравнение гармонического колебания

Рассмотрим простейшую колебательную систему: шарик массой "m" подвешен на пружине.

В этом случае упругая сила F₁ уравновешивает силу тяжести mg. Если сместить шарик на расстояние "х", то на него будет действовать большая упругая сила (F₁ + F). Изменение упругой силы по закону Гука пропорционально изменению длины пружины или смещениюшарика "х" : F = - kx (1), где k - жесткость пружины. Знак "-" отражает то обстоятельство, что смещение и сила имеют противоположные направления. Сила F обладает следующими свойствами:

1) она пропорциональна смещению шарика из положения равновесия;

2) она всегда направлена к положению равновесия.

В нашем примере сила по своей природе упругая. Может случиться, что сила иного происхождения обнаруживает такую же закономерность, то есть оказывается равной - kx. Силы такого вида, неупругие по природе, но аналогичные по свойствам силам, возникающим при малых деформациях упругих тел, называют квазиупругими.

Уравнение второго закона Ньютона для шарика имеет вид:

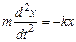, или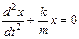

Так как "k" и "m" - обе величины положительные, то их отношение можно приравнять квадрату некоторой величины "w₀ ", т.е. мы можем

ввести обозначение 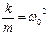. Тогда получим 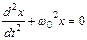. Таким образом, движение шарика под действием силы вида (1) описывается линейным однородным дифференциальным уравнением второго

порядка.

Легко убедиться подстановкой, что решение уравнения имеет вид: x = Acos( w₀ t + a₀ ), (2)

где (w₀ t + a₀ ) = a - фаза колебаний;

a₀- начальная фаза при t = 0;

w₀- круговая частота колебаний;

A - их амплитуда.

Итак, смещение x изменяется со временем по закону косинуса.

Следовательно, движение системы, находящейся под действием силы вида f = - kx, представляет собой гармоническое колебание.

График гармонического колебания показан на рисунке.

Период этих колебаний находится из формулы: 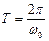. Для пружинного маятника получаем: 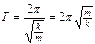.Круговая частота связана с обычной n соотношением: .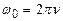