Вынужденный механические колебания. Дифференциальное уравнение и его решение. Резонанс.

В случае вынужденных колебаний система колеблется под действием внешней (вынуждающей) силы, и за счет работы этой силы периодически компенсируются потери энергии системы. Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы Определим амплитуду вынужденных колебаний тела массой m, считая колебания незатухающими вследствие постоянно действующей силы .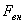

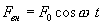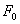Пусть эта сила изменяется со временем по закону , где амплитуда вынуждающей силы 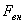. Возвращающая сила 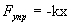и сила сопротивления 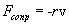Тогда второй закон Ньютона можно записать в следующем виде:

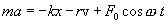
или

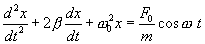(7.21)

Предположим, что возникающее под действием силы установившиеся вынужденные колебания системы также являются гармоническими: 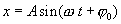(7.22) причем их циклическая частота равна циклической частоте ω вынуждающей силы.

Дифференцируя два раза (7.22) и подставляя в (7.21), получим

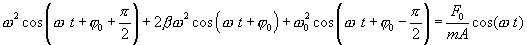
Обозначим: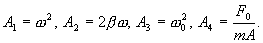

Тогда последнее равенство можно записать в следующем виде:

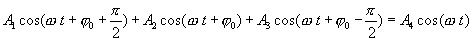
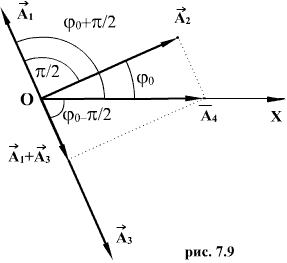
Правую часть этого выражения можно рассматривать как уравнение некоторого гармонического колебания, получившегося при сложении трех гармонических колебаний, определяемых слагаемыми левой части этого равенства. Для сложения этих колебаний воспользуемся методом векторных диаграмм. Проведем опорную линию ОХ (рис. 1.9) и отложим под углами, соответствующими начальным фазам всех четырех колебаний векторы 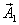, , 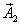, 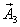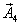их амплитуды таким образом, чтобы

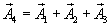
Из рис. 7.9 видно, что 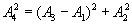Подставляя в последнее значения соответствующих амплитуд (1.22), получим:

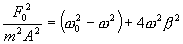
отсюда

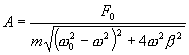(7.23)

Амплитуда установившихся вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы F₀, обратно пропорциональна массе m системы и уменьшается с увеличением коэффициента затухания β. При постоянных F₀, m и β амплитуда зависит только от соотношения циклических частот вынуждающей силы β и свободных незатухающих колебаний системы 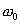. При циклической частоте вынуждающей силы ω=0 амплитуда колебаний 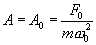. В этом случае колебания не совершаются и смещение при вынужденных колебаниях равно статической деформации под действием постоянной силы F₀:

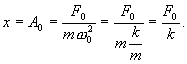
Поэтому отклонение A₀ иногда называют статической амплитудой.

Если нет диссипации т.е β=0, то амплитуда колебаний

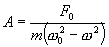
растет с увеличением циклической частоты ω вынуждающей силы F_вн и при 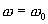становится бесконечно большой (рис. 7.10). При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем

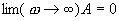
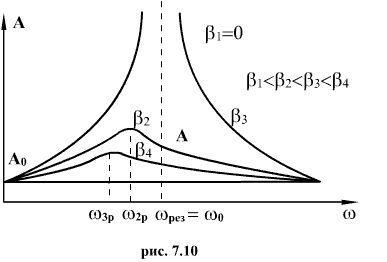
Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы 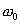называется резонансом.

Если затухание существует 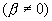то амплитуда вынужденных колебаний достигает максимального значения, когда знаменатель правой части для уравнения (7.23) достигает минимума. Приравнивая нулю первую производную по ω от подкоренного выражения, получим условие его минимума, для которого 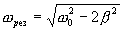, где 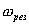- называют резонансной частотой. 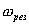обозначает то значение циклической частоты ω вынуждающей силы, при котором .

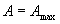Из последней формулы следует, что для консервативной системы 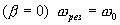, а для диссипативной системы 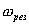несколько меньше собственной циклический частоты. С увеличением коэффициента затухания ω явление резонанса проявляется все слабее, и, наконец при 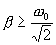исчезает совсем.

Явление резонанса используется для усиления колебаний, например, электромагнитных. Однако при конструировании различных машин и сооружений необходимо учитывать даже самую небольшую периодическую силу с тем, чтобы предотвратить нежелательные последствия резонанса.