Гармонические колебания и их характеристики. Дифференциальное уравнение гармонических колебаний

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

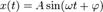
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, 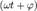ω — циклическая частота колебаний, — полная фаза колебаний, фи — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

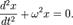
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Потенциальная энергия колеб.

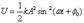
Кинетическая энергия

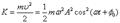
Полная энергия

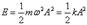
Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания.

Пружинный, физический и математический маятники.

1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид

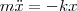
или

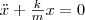
Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω₀t+φ) с циклической частотой

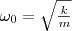(2)

и периодом

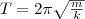(3)

Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна

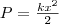
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).

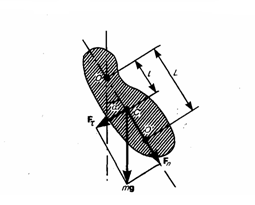
Рис.1

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы

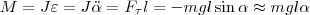(4)

где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, F_τ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления F_τ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как

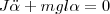
или

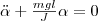
Принимая

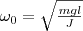(5)

получим уравнение

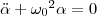
идентичное с (1), решение которого (1) найдем и запишем как:

(6)

Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом

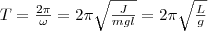(7)

где введена величина L=J/(ml) — приведенная длина физического маятника.

Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 1). Применяя теорему Штейнера для момента инерции оси, найдем

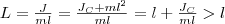
т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.

3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника

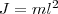(8)

где l — длина маятника.

Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника

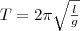(9)

Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.