Порядок выполнения работы

1. Получить и при необходимости согласовать с преподавателем задание.

2. Изучить теоретический материал, пользуясь руководством и рекомендованной литературой (1час).

3. Записать бигармоническое уравнение и граничные условия задачи (0,25 часа).

4. Записать выражения для изгибающих момента и прогиба пластинки (0,25 часа).

5. Записать уравнение Софи Жермен и граничные условия с использованием конечно-элементных аналогов (0,5 часа).

6. Записать систему алгебраических уравнений МКЭ в матричном виде (0,25 часа).

7. Подготовить исходные данные для ПЭВМ по двум вариантам опирания и действии распределенной нагрузки (0,5 часа).

8. Выполнить расчеты пластинки на изгиб для двух вариантов опирания

по программе «Лира 9.0», описание которой приведено в приложении.

9. Построить в заданных сечениях пластины эпюры прогиба W иизгибающих моментов для двух вариантов расчета (0,5 часа).

10. Провести расчет пластинки методом конечных разностей (0,5 часа).

11. Сопоставить решения МКЭ с данными расчетов МКР и сделать соответствующие выводы (0,5 часа).

На выполнение расчетно-графической работы затрачивается примерно 5 часов из времени, отведенного на самостоятельную работу студента. Срок представления оформленной работы составляет три недели с момента выдачи задания.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА О РАБОТЕ

Отчет о работе должен выполняться в соответствии с приведенными примерами расчета и содержать следующие разделы:

- вариант задания;

- постановка задачи;

- запись уравнения Софи Жермен и граничных условий;

- запись уравнения Софи Жермен и граничных условий с использованием конечно-элементных аналогов;

- запись системы А*j = В линейных алгебраических уравнений МКЭ в табличной форме;

- результаты расчетов на ПЭВМ МКЭ в виде эпюр прогиба W и изгибающих моментов для двух вариантов опирания пластинок;

- результаты расчета пластинки методом конечных разностей (МКР);

- сопоставление решения МО и решения МКР.

При оформлении работы численные результаты необходимо иллюстрировать чертежг.ми, выполненными в масштабе с использованием чертежных принадлежностей или компьютерной графики.

Работа оформляется на одной стороне листов формата А4.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие допущения принимаются в теории тонких пластинок?

2. Как выражаются деформации пластинки через ее прогиб?

3. Как записывается дифференциальное уравнение Софи Жермен изгиба элемента пластинки?

4. Как записываются граничные условия для свободной от закреплений стороны контура пластинки?

5. Как формулируются граничные условия на защемленных сторонах контура пластинки?

6. Каковы граничные условия на шарнирно опертых сторонах контура пластинки?

7. В чем особенности применения МКЭ к расчету пластинок?

8. Каковы преимущества использования МКЭ по сравнению с другими методами расчета пластинок?

9. На какие конечные элементы можно разбить прямоугольную пластинку?

10. Какие конечные элементы необходимо использовать для пластинок со сложным контуром?

11. Как записывается система линейных алгебраических уравнений (СЛАУ) зависимости смещений узлов КЭ от узловых сил?

12. Какой вид имеет СЛАУ связи смещений узлов от узловых сил для всей пластинки?

13. Какие требования предъявляются к аппроксимирующим функциям в МКЭ по методу перемещений?

14. Чему равны значения функций формы для различных узлов КЭ?

15. Какова физическая сущность определения вектора узловых перемещений при расчете пластинок МКЭ?

16. Какова последовательность решения задачи изгиба пластинки методом конечных элементов (МКЭ)?

17. Какое количество степеней свободы имеет прямоугольный конечный элемент?

18. Какое количество степеней свободы соответствует треугольному конечному элементу?

19. По каким формулам вычисляются изгибающие и крутящий моменты в пластинке?

20. По каким формулам вычисляются напряжения σ_x, σ_y, τ_xy в пластинке?

21. Элементами каких инженерных сооружений являются пластинки?
ВАРИАНТЫ ЗАДАНИЙ

Схема закрепления пластинок на контуре - цифра 1

«0» - свободный край пластинки,

«1» - шарнирное опирание края пластинки,

«2» - жесткая заделка края пластинки.

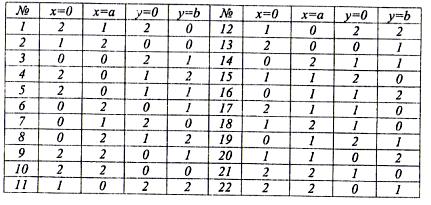
Схема нагружения пластинок - цифра 2

1. равномерная нагрузка q=const по всей поверхности,

2. нагрузка q=const при 0<х<а/2,

3. нагрузка q=const при а/2<х<а,

4. нагрузка q-=const при 0<у<Ь/2,

5. нагрузка q^consl при b/2<y<b,

6. нагрузка q=const при 0<х<а/2, 0<у<Ь/2,

7. нагрузка q=const при 0<х<а/2, b/2<y<b,

8. нагрузка q=const при а/2<х<а, 0<у<Ь/2,

9. нагрузка q=const при а/2<х<а, b/2<y<b.

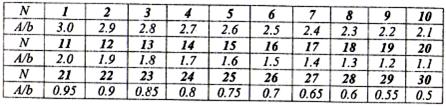
Соотношение сторон пластинок - цифра 3

Приложение