Т1 и Т2 - температуры горячего и холодного источников тепла
I.
II. ТЕРМОДИНАМИКА.
1. Основные понятия, определения и законы термодинамики
Термодинамика – это наука, о взаимных превращениях различных видов энергии.
Термодинамика (от гр. Therme – тепло и dinamikos - силовой) – наука о соотношении между теплом, работой и физико-химическими свойствами систем.
Система – любая совокупность материальных тел внутри заданных границ. В общем случае система взаимодействует с окружающей средой.
Термодинамика как самостоятельная наука выделилась из физики с середине 19 века.
Раздел термодинамики, главной проблемой которого является превращение тепловой энергии в механическую, называется – Технической термодинамикой, а машины используемые для этой цели – тепловыми двигателями.
Типы тепловых двигателей:
1. Паровые турбины (ТЭЦ, морские суда)
2. Паровые машины (Вытеснены другими)
3. Двигатели внутреннего сгорания /д. в. с./ (Транспорт)
4. Газовые турбины (Небольшая мощность)
5. Реактивные двигатели (Для больших скоростей)
Для всех тепловых двигателей необходимо затрачивать тепло.
80 % получаемой энергии человечество получает за счет сжигания топлива.
На очереди стоит применение регулируемой термоядерной реакции.
Преобразование тепловой энергии в электрическую непосредственно:
ТЭГ – термоэлектро генератор
ТИГ – термоионный генератор
МГДГ – магнитогидравлический генератор
ХЭГ – химикоэлектро генератор
Другой проблемой технической термодинамики является проблема получения холода за счет затраты работы. Такие машины называются холодильниками.
Методы исследования тепловых двигателей аналогичны методам исследования холодильных машин.
Основные параметры. Уравнения состояния.
Система – это объект термодинамического исследования. Может быть открытой (существует обмен веществом и энергией с окружающей средой), закрытой (отсутствует обмен веществом с окружающей средой), адиабатной (отсутствует энергообмен с окружающей средой).
Рабочее тело – это посредник служащий для получения работы, теплоты, холода. Может быть в газообразном и твердом виде.
Независимым параметром состояния системы является степень свободы, находящаяся в термодинамическом равновесии, и которую можно изменять в определенных пределах так, чтобы сохранились все фазы, имевшиеся в системе, и не появились какие-либо новые фазы. Например, двигатель внутреннего сгорания – это закрытая система, имеющая две степени свободы, т.к. топливо сжигается непосредственно в рабочей полости, а выделяющаяся при этом теплота преобразуется в механическую работу.
Рассмотрим основные параметры состояния системы.
Абсолютное давление: (измеряется в Па, МПа, кПа.)
P = Pатм + Pмех
P = Pатм - Pвак
Pвак – давление вакуметра.
1 кгс/см2 = 9,81 ´ 104 Па;
1 мм рт. ст. = 133,32 Па;
1 мм вод. ст. = 9.81 Па;
1 бар = 105 Па = 100 кПа = 0,1 МПа;
1 нормальная атмосфера = 101325 Па;
Абсолютная температура (Кельвин), за ноль принята точка абсолютного нуля:
T = t + 273,15 K
Если изменение температуры равно нулю (ΔТ = 0) , то теплообмен между телами невозможен.
Удельный объем:
v = V/ m (м3/кг);
Плотность
r = 1/v = m/V (кг/м3)
Уравнение состояния реального газа
pv/RT = z .
где z = 1 + ar + br2 + cr3 – характеристика сжимаемости (функция плотности),
a, b, c – вириальные коэффициенты, которые зависят от состояния газа и температуры.
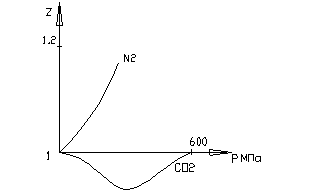 |
Рис. 1. Зависимость сжимаемости газов от температуры
При малых давлениях, для идеального газа принимают z = 1, тогда уравнение состояния принимает форму Менделеева-Клапейрона
pv = RT,
или pV = mRT,
где R – газовая постоянная одного килограмма газа 8314/m[Дж/кг´К]
mR = 8314 – работа одного моля газа, совершаемая при нагреве на один градус.
Для реальных газов часто уравнение состояния применяется в виде уравнения Ван-Дер-Ваальса:
(p + a/v2)(v - b) = RT
где a/v2, b – поправки на взаимное влияние молекул и их размеров.
2. Смеси идеальных газов
Рассмотрим смеси идеальных газов не вступающих в химические реакции. Даны молекулярные веса и газовые постоянные соответственно смеси и её компонентов: m, R, mi, Ri
Каждый из этих компонентов оказывает свое давление, причём давление смеси определяется законом Дальтона.
p = Spi
Vi – парциальный объем – это тот объем, который занимал бы компонент при давлении и температуре смеси (Vi ® p,T).
Состав смеси можно задавать:
1. Объемными долями ri = Vi/V , в смеси: Sri = 1
Vip = piVi pi = rip
2. Молярными долями Mi = m/mi , в смеси: M = SMi ,
молярная доля компонентов: Yi = Mi/M SYi = 1
3. Массовыми долями: qi =mi/m m = Smi Sqi = 1
Молекулярный вес смеси
mсмеси = Smi/SM Þ Газовая постоянная смеси R = SqiRi , mi - масса компонента.
Пример 1.
Сухой воздух, состоит по объему из 21% О2; 79% N2. Определить газовую постоянную и парциальные давления R; pi;
PСМ=760 мм рт. ст.
Решение:
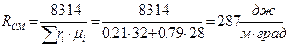
 мм рт. ст.
мм рт. ст.
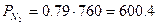 мм рт. ст.
мм рт. ст.
Пример 2.
Определить массовый мольный состав воздуха.
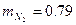
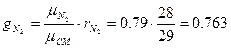
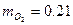
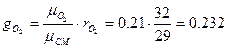
Понятие о равновесном и обратимом процессах.
Уравнение состояния справедливо для газа, находящегося в покое. Такое состояние называется равновесным, т.е. когда параметры одинаковы по всему объему.
Для выведения его из этого состояния, необходимо воздействие окружающей среды, т.е. необходим процесс. Процесс – любое изменение состояния рабочего тела.
В зависимости от взаимодействия со средой процесс может быть равновесным и неравновесным.
Равновесный термодинамический процесс – когда в любой момент рабочее тело находится в равновесном состоянии.
1. Бесконечно малая разность давлений рабочего тела и окружающей среды.
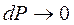
2. Бесконечно малая разность температур рабочего тела и окружающей среды.
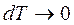
3. Равновесный процесс должен протекать бесконечно медленно.
Для изменения направления равновесного процесса, достаточно только изменить знак у dP и dT. При свершении такого процесса в одном, затем в другом направлении в системе не произойдет никаких изменений. Поэтому равновесный процесс при отсутствии трения называется обратимым процессом.
В теоретических циклах все процессы обратимы.
В реальных двигателях процессы считают равновесными или квазиравновесными, но в следствии трения этот процесс необратим.
Энергетические характеристики термодинамической системы
· Энергия - Е
Для системы, имеющей массу m полная энергия складывается из кинетической, потенциальной и внутренней
Е = ЕК + ЕП + U,
Соответственно для одного килограмма газа – удельная энергия:
е = ек + еп + u
Кинетическая энергия представляет собой энергию движущихся молекул:
ЕК = mv2/2
Потенциальная энергия характеризуется тем, что её изменение может происходить лишь при перемещении рабочего тела, находящегося в силовом поле.
Внутренняя энергия определяется взаимоотношением частиц рабочего тела и является функцией состояния. U = U(T,V) – функция температуры и объема.
Изменение внутренней энергии: ∆U = U2 – U1,
Для сложной системы внутренняя энергия складывается: U = åUi.
Внешняя работа газа в равновесном процессе.
Работа и теплота не являются видами энергии, а являются способами обмена энергии системы с другими телами.
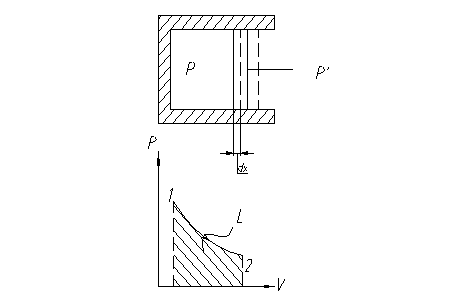
Рассмотрим пример перемещения поршня в цилиндре под действием нагреваемого газа (процесс 1-2).
Элементарная работа совершаемая газом равна произведению давления газа в цилиндре на площадь поршня и элементарное перемещение
dL = pfdx = pd
Полная работа находится инегрированием по перемещению поршня или изменению объёма.
L = ò pfdx = òpdv,
Выделяемое или подводимое тепло
dQ = mCdt
Тепло и работа являются функциями термодинамического процесса
· Энтальпия – Н характеризует запас энергии в системе и для термодинамических систем она совпадает с энергией.
Н = Е.
Если система подвижна, то энтальпия равна сумме внутренней энергии и совершаемой работы
Н = U + Pdv
Функции состояния и функции процесса.
Функции состояния: Все параметры состояния ( 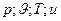 )
)
Функции процесса: Работа и тепло.
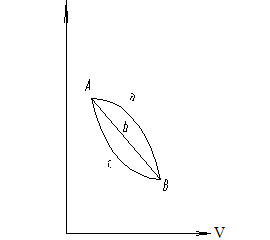
1. Установим математические характеристики функций состояния на примере U:
DU – полный дифференциал, его свойство то, что 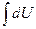 - не зависит от пути процесса, а зависит только от начального и конечного состояния.
- не зависит от пути процесса, а зависит только от начального и конечного состояния.
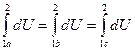 ,
, 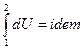 следствие
следствие 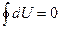
2. Функции процесса – например работа:
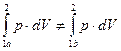
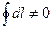
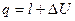 , то
, то 
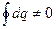 , т.е. dq – не является полным дифференциалом.
, т.е. dq – не является полным дифференциалом.
Энтропия как параметр состояния идеального газа.
Понятие энтропия было введено в науку в середине 19 века и может быть определено в качестве обобщённой координаты при тепловом воздействии на систему по аналогии с изменением объёма при механическом воздействии, что видно из таблицы.
| Воздействие | Энергия воздействия | Движущая сила | Обобщенная координата |
| деформационное | dl | P | dV |
| тепловое | dq | T | ds |
На основе первого закона для идеального газа и обратимого процесса (используя уравнение Менделеева – Клайперона и обратимость работы)
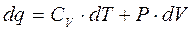
Тепло q – не является параметром состояния.
dq – можно представить как полный дифференциал, подобрав соответствующий интегральный множитель или делитель, например температуру Т.
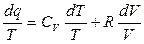 (
( 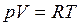 )
)
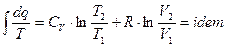
Правая часть не зависит от пути интегрирования.
Интеграл постоянный не зависит от вида процесса.
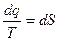 - обладает свойством полного дифференциала, а S – параметр состояния газа, энтропия.
- обладает свойством полного дифференциала, а S – параметр состояния газа, энтропия.
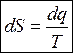
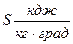
После интегрирования от первого состояния до второго получаем
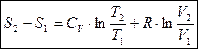
Для массы М, кг 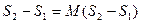
Энтропия смеси равна сумме энтропий составляющих при парциальных давлениях и температуре смеси.
Энтропия используется для графического исследования процессов, так как площадь под кривой, изображающей процесс эквивалентна подводимому к рабочему телу теплу.
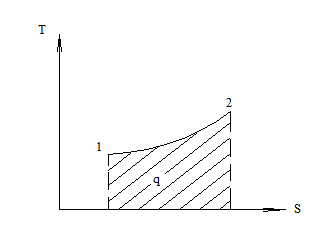
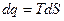 ;
; 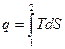
Т>0
Если 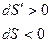 , то
, то 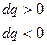
4. Теплоемкость идеальных газов и их смесей.
Теплоемкость – это количество тепла необходимое для нагрева 1 кг вещества на 1°. Для газа может быть изохорной (процесс происходит в неизменном объеме) и изобарной (процесс происходит при одинаковом давлении). Рассмотрим пример: нагревание газа в цилиндре при постоянном и переменном объёме.
 |  |





 В первом случае всё тепло затрачивается на
В первом случае всё тепло затрачивается на
изменение внутренней энергии,
V = const – Cv ® DU
Во втором - на изменение внутренней энергии и
совершение работы.
p = const – Cp ® DU + DL
Разность изобарной и изохорной теплоёмкостей представляет работу одного килограмма газа, совершаемую при его нагревании на один градус иявляется газовой постоянной
Cp - Cv = R
Универсальная газовая постоянная для одного моля газа
m(Cp - Cv) = 8314 Дж/мольК
Соотношение между изобарной и изохорной теплоемкостями зависит от атомности газа, в частности от числа степеней свободы его молекул.
1 ат. – 3 степени свободы все за счет поступательного движения.
2 ат. – 5 степеней свободы: 3 за счет поступательного движения + 2 за счет вращательного.
3 ат. – 6 степеней свободы: 3 за счет поступательного движения + 3 за счет вращательного.
Показатель адиабаты, равный отношению изобарной и изохорной теплоёмкостей зависит от числа атомов в молекуле
k = Cp/Cv
k1 ат = 1,67; k2 ат = 1,40; k3 ат = 1,33; kвоздуха = 1,4.
Теплоёмкости зависят от температуры и давления, что видно из приведённых ниже связей
Cv =Cvид + DCv
Cp = Cpид + DCp
DCv; DCp = f(p) Cvид ; Cpид = f(T)
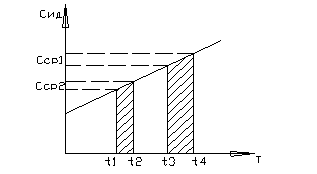
Количество тепла, необходимое для нагрева одного килограмма газа на одинаковое количество градусов в различном температурном диапазоне неодинаково, что видно из рис.
Dq3 - 4 > Dq1 – 2
t4 - t3 = t2 - t1
Задачи можно решать по средней теплоемкости в данном интервале температур. Теплоемкость газовой смеси определяется теплоемкостями входящих в них компонентов массовыми и объемными долями.
5. Первый закон термодинамики.
В термодинамике принято теплоту подведенную к рабочему телу считать положительной, а отведенную от него отрицательной. Совершаемая газом работа считается положительной, отводимая – отрицательная. Рассмотрим закрытую систему, для которой первый закон термодинамики формулируется:
Подводимое к газу тепло расходуется на превращение внутренней энергии и на совершение работы
dq = du + dl (1),
или
dq = CudT + pdV (2)
для 1 кг газа 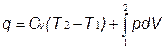 (3).
(3).
Результат интегрирования в выражении (3) зависит от характера термодинамического процесса.
dq = CpdT – UdP.
Для потока газа (открытой системы) первый закон термодинамики:
Подведенное к газу тепло идет на изменение внутренней энергии, совершение работы, изменение кинетической энергии и изменение потенциальной энергии положения.

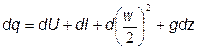
w1 , w2 – скорости газа в 1-м и 2-м сечениях
g – ускорение свободного падения.
6. Политропный процесс.
Изменение внутренней энергии пропорционально подводимому или отводимому теплу.
dU = jdq, j (- ¥; +¥).
Если j = const – процесс политропный – процесс, в котором доля тепла идущего на изменение внутренней энергии есть величина постоянная.
dq = dU + I = jdq +l
dq = CdT , С – теплоемкость политропного процесса,
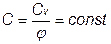 , pvn = const,
, pvn = const,
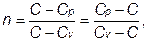 nÎ(- ¥; +¥) – показатель политропы.
nÎ(- ¥; +¥) – показатель политропы.
Рассмотрим расчет работы и внутренней энергии для политропного процесса.
 - связываем параметры газа. Из этой системы можно исключить два параметра, оставив два.
- связываем параметры газа. Из этой системы можно исключить два параметра, оставив два.
Заменим удельный объём на плотность 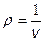 [кг/м3] – если в термодинамике принято оперировать удельным объемом, то в газовой динамике с плотностью.
[кг/м3] – если в термодинамике принято оперировать удельным объемом, то в газовой динамике с плотностью.
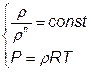
Решив указанную систему можно получить соотношения параметров для политропного процесса 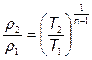
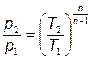 , используя которые получим работу расширения для 1 килограмма газа
, используя которые получим работу расширения для 1 килограмма газа
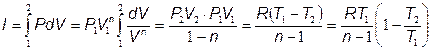
следовательно работа политропного процесса:
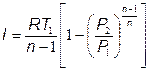 ;
;
изменение внутренней энергии DU = Cv (T2 – T1);
тепло процесса q = DU + l.
Рассмотрим графики основных термодинамических процессов в координатах p-V и T-s.
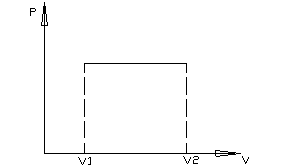
Изохорный -Это процесс протекающий без изменения объема газа.
V = const.
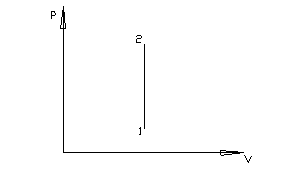
q = DU = Сv(T2 – T1).
Площадь под линией в координатах p-V характеризует совершаемую работу.
V = const 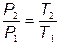
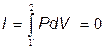
При изохорном процессе невозможно получить полезную работу.
 |
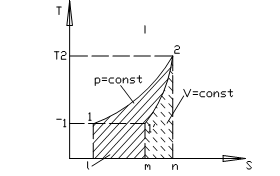 Изобарный - процесс, протекающий при постоянном давлении.
Изобарный - процесс, протекающий при постоянном давлении. 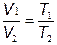 ;
; 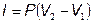 ;
; 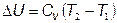 ;
; 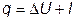 ;
;
Уравнение Майера для определения подводимого в изобарном процеесе тепла.
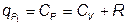
Изотермический - процесс происходящий без изменения температуры.
Т = const.
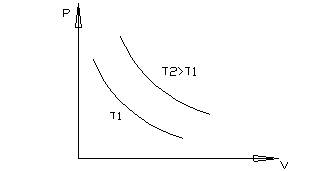 |
pV = RT = const
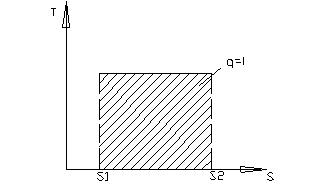 |
p1V1 = p2V2
Т1 и Т2 – разные температуры процессов.
Работа рассчитывается по формуле
 .
.
Адиабатный 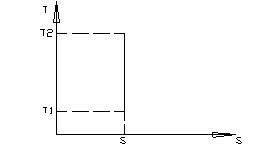 – это процесс, происходящий без теплообмена с окружающей средой.
– это процесс, происходящий без теплообмена с окружающей средой.
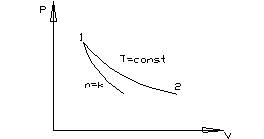
pvk = const, 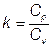 - показатель диабаты (для воздуха k = 1,4); Работа при адиабатном процессе равна изменению внутренней энергии рабочего тела
- показатель диабаты (для воздуха k = 1,4); Работа при адиабатном процессе равна изменению внутренней энергии рабочего тела
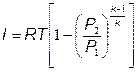 ; l = -DU;
; l = -DU;
T¯ Þ l.
Особенности процессов в тепловых машинах.
Особенность тепловых машин: рабочее тело проходит через машину. Т.е. любая тепловая машина – проточная система. Поэтому необходимо ввести новые характеристики термодинамических процессов.
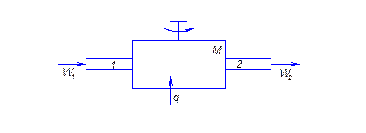
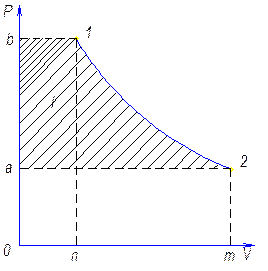
Рассмотрим общую схему тепловой машины, конкретно – тепловой двигатель. В трубопровод 1 поступает рабочее тело P1,V1,T1( и т.д. ). В машине М это тело деформируется, затем поступает в выпускной трубопровод 2 с параметрами P2, V2, T2 ( и т.д. ). К рабочему телу подводится тепло q, с выходного вала получается работа.
Несколько изменим схему
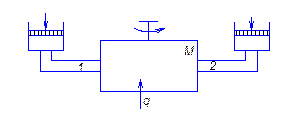
Внутренняя энергия газа во впускном трубопроводе 1 – U1. Внутренняя энергия газа в выпускном трубопроводе 2 – U2 полностью P;T;V.
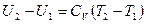 - для идеального газа.
- для идеального газа.
Работа деформации раскладывается на составляющие:
- внешне полезная;
- располагаемая
- техническая работа.
Внешне полезной lп называется та часть от общей работы которая идет например на вращение вала или другую рабочую операцию.
В общем случае часть работы расходуется на увеличение кинетической энергии рабочего тела, это есть располагаемая работа газа lр, т.к. ее можно превратить в работу (использовав турбину и т.д.).
Если в поршневых и турбинных двигателях главный результат lп, то в реактивных двигателях главный результат – lр. Эта располагаемая работа реализуется в процессе полета ракет или летательных аппаратов.
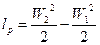
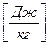
Сумма внешне полезной и располагаемой работ называется технической работой.
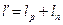
Работа вытеснения.
Проходя через машину газ совершает работу. При поступлении совершается работа вталкивания, т.к. давление в трубопроводе 1 постоянно, то величину работы можно посчитать:
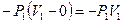 - она отрицательна, т.к. она совершается над рабочим телом.
- она отрицательна, т.к. она совершается над рабочим телом.
На выходе из машины совершается работа выталкивания:
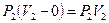
Их алгебраическая сумма – работа вытеснения.
Вся работа деформации l состоит из:
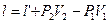
Изображение технической работы в диаграмме P-V.
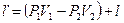

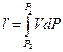
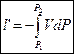
Рассмотрим соотношение между работой деформации l ии технической работой l’:
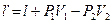
Для внешней работы в политропном процессе:
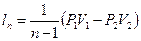
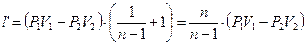
Сравним l и l’:
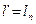
II-й закон термодинамики.
I-й закон не касается условий, при которых возможен переход тепла в работу. Опыт показывает, что если ТА > ТВ , то тепло идет только от А к В, причем при ТА = ТВ теплообмен прекращается. Исходя из I-го закона термодинамики непонятно почему в тепловых двигателях все подведенное тепло не превращается в работу (h < 1), хотя известно, что работа превращается в тепло на 100%.
Все эти взаимные превращения рассматриваются II-м законом термодинамики, он ограничивает действие I-го закона.
1) Установление условий превращения тепла в работу.
2) Установление степеней совершенства этого превращения.
Формулировка II-го закона термодинамики.
Формулировка Карно(для тепловых двигателей):
Всюду, где имеется разность температур, возможно возникновение работы.
Т.е. тепло не может всё превращаться в работу, часть тепла переходит к источнику с низкой Т°.
Формулировка Оствольда:
Осуществление вечного двигателя II-го рода (кпд =100%) невозможно.
Формулировка …:
Тепло не может переходить само собой от тела более холодного к более нагретому.
Т.е. для этого перехода необходимо затратить работу, например в холодильных машинах.
Формулировка Ломоносова:
Холодное тело В, погруженное в тело А не может воспринять большую степень тепла, чем имеет А.
Круговые процессы (циклы).
Круговым процессом называют всякий процесс, в результате которого рабочее тело приходит в исходное состояние.
Рабочие процессы в тепловых машинах рассматриваются как циклы,
Паротурбинная установка – очевидно. Двигатель внутреннего сгорания – менее очевидный цикл, нужно в систему включать атмосферу, являющуюся холодильником.
Для цикла изменение внутренней энергии DU=0, всё подводимое тепло расходуется на совершение работы q=l.
Все термодинамические циклы разделяются на 2 группы:
а) прямые – тепловые двигатели.
б) обратные – холодильные машины.
Прямой цикл и его характеристика.
Это цикл, который в координатных осях p-V совершается по часовой стрелке.
В каждом цикле можно выделить 2 группы процессов:
а) расширения DV > 0
б) сжатия DV < 0
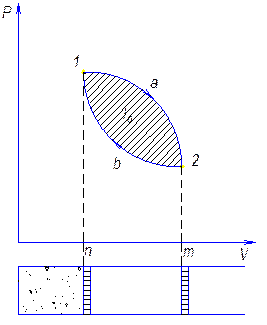
а) работа расширения соответствует площади под кривой lрасш=1a2mn, онаограничена линейным перемещением поршня. Затем необходимо вернуть поршень в исходное положение, а рабочее тело в исходное состояние, т.е. необходимо совершить процесс сжатия.
б) работа сжатия соответствует площади под кривой lсж=2b1nm
lрасш>lсж – в прямом цикле,
lрасш-lсж=l0 – полезная работа цикла.
Рассмотрим цикл в диаграмме T – S.
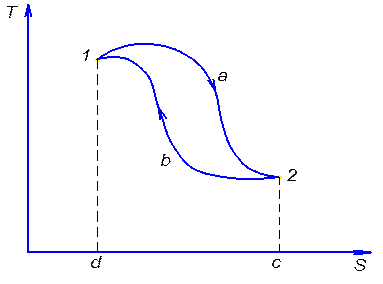
1а2 – тепло подводится
q1=1a2сd – подводимое тепло
q2=2b1dc – отводимое тепло
Видно, что для совершения цикла тепло надо и отводить и подводить.
DU=0 – т.к. это цикл
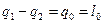 - на основании I-го закона термодинамики
- на основании I-го закона термодинамики
q0 – полезная теплота цикла
Характеристикой прямого цикла является термический КПД цикла.
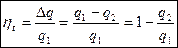
Это есть отношение количества тепла, превращенного в работу, ко всему подводимому за цикл теплу.
Среднее давление цикла:
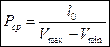
Цикл Карно.
Из всех возможных циклов он обладает максимальным термическим КПД. Выбирая наивыгоднейшие процессы, образующих цикл, Карно доказал, что лучшим является обратимый цикл, состоящий из 2-х изотерм и 2-х адиабат.
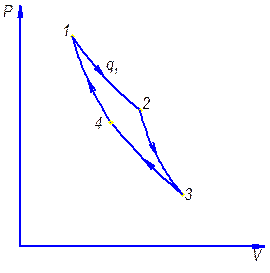
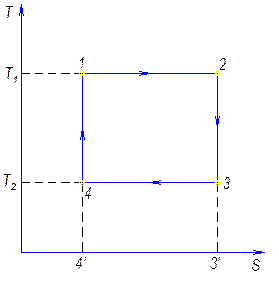
Т1 и Т2 - температуры горячего и холодного источников тепла
1-2 – изотерма с подводом тепла
2-3 – адиабата расширения
3-4 – изотерма сжатия с отводом тепла
4-1 – адиабата сжатия
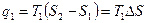
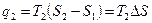
Термический кпд цикла Карно
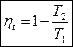 - зависит только от Т1 и Т2
- зависит только от Т1 и Т2
ht < 1
Так для температуры камеры сгорания реактивного двигателя Т1 = 2000 К, и температуры холодильника (атмосферы) Т2 = 293 К:
ht = 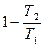 ;
;
ht = 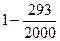 = 0,8535 = 85,35%
= 0,8535 = 85,35%
