Раздел 4. Кривые второго порядка
Алгебраическая кривая – плоская кривая, координаты точек которой удовлетворяют уравнению F(x, y) = 0, где левая часть – многочлен; степень многочлена называется порядком алгебраической кривой.
Большая ось эллипса – длина хорды эллипса, расположенная на фокальной оси эллипса.
Большая полуось эллипса – половина большой оси эллипса.
Гипербола – плоская кривая (алгебраическая кривая второго порядка), каноническое уравнение которой в декартовых координатах имеет вид: 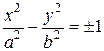 . См. Равнобочная гипербола.
. См. Равнобочная гипербола.
Главные направления квадратичной формы – направления осей симметрии соответствующей кривой второго порядка; квадратичная форма имеет два главных направления.
Действительная ось гиперболы – длина отрезка между вершинами гиперболы.
Действительная полуось гиперболы – половина действительной оси гиперболы.
Канонический вид квадратичной формы – вид квадратичной формы, содержащей только квадраты переменных, т.е. F(x, y) = l1x2 + l2y2.
Каноническое уравнение кривой второго порядка - уравнение кривой в декартовых координатах, в котором хотя бы одна переменная была в квадрате, и система координат расположена определенным образом по отношению к к кривой (см. соответствующую таблицу).
Квадратичная форма – однородный многочлен второй степени, в данном разделе содержит две переменные: F(x, y) = a11x2 + 2a12xy + a22y2.
Коническое сечение см. Кривая второго порядка.
Кривая второго порядка (Линия второго порядка, коническое сечение) – алгебраическая кривая, уравнение которой в декартовых координатах содержит одну или обе координаты в квадрате.
Кривая на плоскостисм. Линия на плоскости.
Круг – часть плоскости, ограниченная окружностью.
Линия на плоскости (Кривая на плоскости) – множество точек плоскости, координаты которых удовлетворяют некоторому уравнению F(x, y) = 0.
Малая ось эллипса – длина хорды эллипса, расположенной на оси перпендикулярной фокальной оси эллипса.
Малая полуось эллипса – половина малой оси эллипса.
Матрица квадратичной формы – симметричная матрица, составленная из коэффициентов квадратичной формы (см. соответствующую таблицу).
Матрица поворота к главным направлениям квадратичной формы (кривой второго порядка) – матрица, элементами которой являются тригонометрические функции и которая находится по определенному правилу (см. соответствующую таблицу).
Мнимая ось гиперболы – ось, сопряженная действительной оси гиперболы.
Мнимая полуось гиперболы – половина мнимой оси гиперболы.
Нецентральная кривая второго порядка - кривая второго порядка, не имеющая центра симметрии; такой кривой является парабола.
Общее уравнение кривой второго порядка – уравнение второй степени, содержащее квадратичную форму, линейную часть и свободный член:
a11x2 + 2a12xy + a22y2 + 2b1x + 2b2y + c = 0.
Окружность – плоская кривая, все точки которой находятся на данном расстоянии от фиксированной точки (центра окружности).
Ось симметрии – прямая, относительно которой симметрично отображаются точки пространства, плоскости или прямой.
Парабола - алгебраическая кривая второго порядка, каноническое уравнение которой в декартовых координатах имеет вид: y2 =2px или x2 =2py.
Параллельный перенос осей координат – переход к новой системе координат, при котором меняется положение начала координат, а направление осей координат и масштаб остаются неизменными.
