Дополнительное задание 1
1.18.Даны матрицы A = 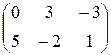 , B =
, B = 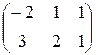 . Найти:
. Найти:
а) 3A + 2B; б) A - B; в) 2A + 4B; г) матрицу X в уравнении 3A + 2X = B.
| 1.19. Найти линейную комбинацию матриц: A – lE, где E – единичная матрица, | A = 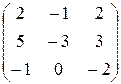 . . | |
| 1.20. Найти произведения AB и BA: | A = 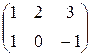 , B = , B = 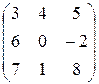 . . | |
Найти произведение матриц:
1.21. 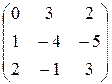 .
. 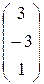 . 1.22.
. 1.22. 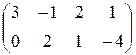 .
. 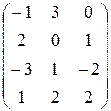 .
.
1.23. 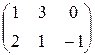 .
. 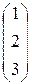 .
. 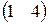 . 1.24.
. 1.24. 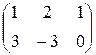 .
. 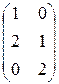 .
.
1.25. 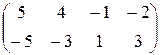 .
. 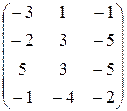 .
.
| 1.26. Вычислить AB, BA, AB - BA, если | A = 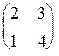 , B = , B = 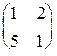 . . | ||
| 1.27. Вычислить AB, BA, AB - BA, если | A = 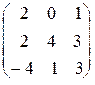 , B = , B = 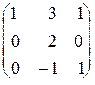 . . | ||
1.28. Найти все матрицы, перестановочные с матрицей 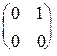 .
.
1.29. Доказать, что A3 = E, где A = 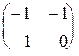 .
.
Найти значение матричного многочлена f(A), соответствующего многочлену f(x): 1.30.f(x) = 2x3- 3x2 + 5, A = 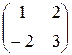 . 1.31.f(x) = x3- 6x2 + 9x + 4, A = . 1.31.f(x) = x3- 6x2 + 9x + 4, A = 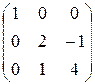 . . | ||
1.32. Показать, что при некотором значении k выполняется равенство M2 - 8M = kE, где E - единичная матрица; M = 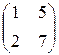 . . | ||
Найти произведения а) AAT и б) ATA: 1.33. A =  . 1.34. A = (1 2 3 4). 1.35. A = . 1.34. A = (1 2 3 4). 1.35. A = 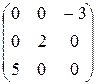 . . |
Ответы к занятию 1
1.2. AB - BA = 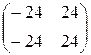 . 1.3.
. 1.3. 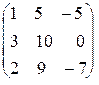 . 1.4.
. 1.4. 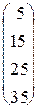 . 1.5.
. 1.5. 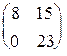 .
.
1.7. - 4; 5. 1.10. AB - BA = 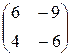 . 1.11.
. 1.11. 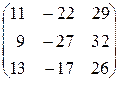 . 1.12.
. 1.12. 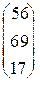 .
.
1.13. 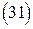 . 1.14.
. 1.14. 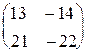 . 1.15.
. 1.15. 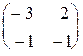 . 1.16.
. 1.16. 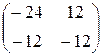 .
.
1.18.X = 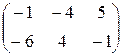 . 1.19.
. 1.19. 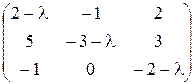 .
.
1.20.AB = 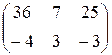 , BA не существует. 1.21.
, BA не существует. 1.21. 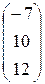 .
.
1.22. . 1.23. .1.24. .1.25. .
1.28. 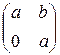 , где a и b - любые числа. 1.30.
, где a и b - любые числа. 1.30. 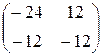 . 1.31.
. 1.31. 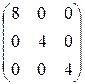 .
.
1.33. а) 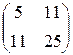 , б)
, б) 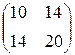 . 1.34. а) (30); б)
. 1.34. а) (30); б) 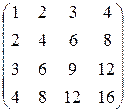 .
.
1.35. а) 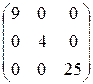 , б)
, б) 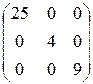 .
.
Занятие 2. Формулы Крамера. Алгебра матриц
Изучаемый материал: формулы (правило) Крамера; виды матриц; линейные операции над матрицами; умножение матриц.
| 1. Правило Крамера | 2.1, 2.2 | 2.7, 2.8, 2.9 | ||
| 2. Линейные операции над матрицами | 2.3 | 2.10 | ||
| 3. Произведение матриц | 2.4, 2.5, 2.6 | 2.11, 2.12, 2.13, 2. 14, 2.15 | ||
Решить системы по правилу Крамера:
2.1. 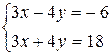 . . | 2.2. 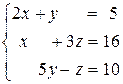 . . | ||||
2.3.Вычислить линейные комбинации матриц: а) A+2B, б) A-B, в) 2A+4B, где A = 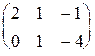 ; B = ; B =  . Вычислить произведение матриц: . Вычислить произведение матриц: | |||||
2.4. 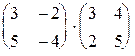 . . | 2.5.  . . | 2.6. 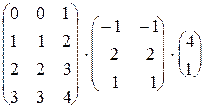 . . | |||
Домашнее задание 2
| Решить системы по правилу Крамера: | ||
2.7. 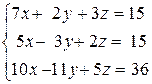 . . | 2.8. 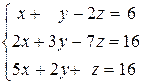 . . | 2.9. 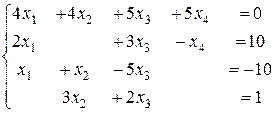 . . |
2.10.Вычислить линейные комбинации матриц: а) 3A+2B, б) 3A-2B, где A = 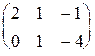 ; B = ; B =  . . |
Вычислить произведение матриц:
