Геометрияның мектептік курсының аксиомалары жайында

Орта мектепке арналған геометрияның жаңа оқулықтарында курстың негізін құруға Σ_W системадан да, Σ_Н системадан да өзгеше система алынған.

Біз VI – VIII кластарға арналған оқулықтарда А.Н.Колмогоровтың редакциясымен берілген планиметрияның аксиомалар системасын қарастырамыз. Мұнда евклид жазықтығының структурасының базасы Е, F, G үш жиыннан тұрады, сонымен бірге 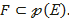Е-нің элементтері – нүктелер, ал F-тің элементтері түзулер (әрбір түзу – Е жиынының белгілі бір бөлімше жиыны) деп аталады. G – қашықтық деп аталатын белгілі бір теріс емес шамалардың жиыны.

Негізгі қатынастар тиістілік қатынас болып табылады және 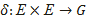бейнелеумен анықталатын тернарлық қатынас болады.

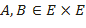элементінде δфункциясын қабылдайтын δ(АВ) мәні А дан В-ге дейінгі қашықтық деп аталады және |АВ| арқылы белгіленеді.

«Арасында жатады» қатынасы былай анықталады: егер Х нүктесі А және В нүктелерінің әрқайсысынан өзгеше болса, онда мына шарттарды қанағаттандырса: |АВ|+|ХВ|=|АВ|, онда Х нүктесі А және В нүктелерінің арасында жатады. Бұл жағдайды біз былай жазамыз: µ(АХВ). Планиметрияның мектептік курсының аксиомалар системасы (мұны Σ_К арқылы белгілейміз) I – V бес топқа бөлінген 12 аксиоманы қамтиды.

Т и і с т і л і к а к с и о м а л а р ы.

І₁. Түзу – нүктелер жиыны.

І₂. Кез келген әр түрлі екі нүктеге сәйкес, оларды қамтитын тек қана бір түзу болады.

І₃. Ең болмағанда бір түзу бар және сол түзудің әрқайсысында ең болмағанда бір нүкте болады.

Қ а ш ы қ т ы қ а к с и о м а л а р ы.

ІІ₁. |АВ|=0↔А=В.

ІІ₂. |АВ|=|ВА|.

ІІ₃. |АС|≤|АВ|+|ВС|,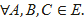

Р е т а к с и о м а л а р ы.

ІІІ₁. ρ түзуінің кез келген О нүктесі ρ\{О} жиынын бос емес L₁, L₂ екі жиынға былай бөледі:

а) 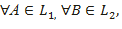мынаны табамыз: µ(АОВ);

б) егер А және В≠А нүктелері L₁, L₂ жиындарының біріне тиісті болса, онда µ(ОАВ) немесе µ(ОВА).

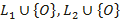жиындарының әрқайсысы, бас нүктесі О болатын сәуле деп аталады. Х≠О нүктесі бар бас нүктесі О болып келген сәулені [ОХ) деп белгілейді.

ІІІ₂. Егер [ОХ) сәуле берілсе, онда 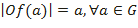болатындай f:G→[ОХ) бейнелеу бар болады.

ІІІ₃. Егер µ(АВС) қатынас орындалса, онда А, В, С нүктелері бір түзуде жатады.

ІІІ₄. Кез келген ρ түзуі Е\ρ жиынын бос емес екі П₁, П₂ жиынға былай бөледі:

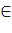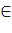а) кез келген А П₁, В П₂ нүктелері ρ түзуімен бөлінген;

б) егер А және В нүктелері П₁, П₂ жиындарының біріне тиісті болса, онда бұл нүктелер ρ түзуімен бөлінген.

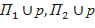жиындарының әрқайсысы р түзуімен шектелген жарты жазықтық деп аталады, ал р түзуі жарты жазықтықтың шекарасы деп аталады.

IV. Ж а з ы қ т ы қ т ы ң қ о з ғ а л ғ ы ш т ы қ а к с и о м а с ы.

Егер |АВ|>0 және |АВ|=|А₁В₁| болса, онда дәл екі ығыстыру бар, олардың әрқайсысы А нүктесін А₁ нүктесіне, ал В нүктесін В₁ нүктесіне көшіреді. Бұл ығыстырулар (АВ) түзуімен шектелген Н жарты жазықтығы (А₁В₁) түзуімен шектелген Н₁, Н₁^’ екі жарты жазықтыққа көшіреді.

V. П а р а л л е л ь д е р а к с и о м а с ы. Берілген нүктеден берілген түзуге параллель бірден артпайтын түзу өтеді.

1 – т е о р е м а. Σ_К 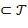(Σ_W).

С а л д а р. Егер нақты сандар арифметикасы қайшылықсыз болса, онда Σ_К аксиомалар системасы да қайшылықсыз болады.

2 – т е о р е м а. Σ_W 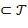(Σ_К).

1 және 2 теоремалардан шығатын салдар.

С а л д а р. Σ_W және Σ_К аксиомалар системасы эквивалентті.

Сфералық геометрия белгілі бір сферада жататын фигуралардың қасиеттерін зерттейді. Осы сфераны S, оның центірін О, радиусын r арқылы белгілелік.

П׀ρ(О, П)< r жазықтығын алалық. Сонда S∩П қиылысуы шеңбер болады, мұны егер О 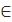П болса, онда үлкен шеңбер, ал егер О 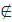П болса, онда кіші шеңбер дейміз.

Сфералық М₀М₁М₂...М_n сынақ ұғымы жазықтығы сынық ұғымы сияқты анықталады, тек түзулердің [М₀М₁],...,[М_n-1M_n] кесінділерінің орнына үлкен шеңберлердің 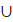М₀М₁,..., 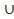М_n-1M_n доғалары алынады.

Егер 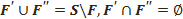болып, мына екі шарт орындалса:

а) 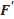(немесе 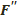) фигураның кез келген екі нүктесін F фигурасымен қиылыспайтын, сфералық сынықпен қосуға болса;

б) егер A 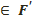, B 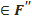болған жағдайда А және В нүктелерін қосатын және және F фигураны қимайтын сфералық сынақ болмаса, онда 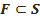фигура 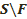фигураны 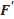, 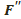екі бөлікке бөледі.

Кез келген 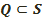үлкен шеңбер 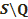фигураны екі бөлікке бөлетінін байқау қиын емес, бұларды 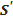және 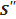арқылы белгілейік. Q шеңбердің П жазықтығының бір жағында жатқанда ↔А және В нүктелері 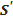, 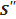фигураларының бірінде жатады.

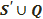және 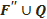фигуралардың әрқайсысы жартылай сфера деп, ал Q үлкен шеңбер осы жартылай сфералардың шеті деп аталады.

А мен В нүктелері – S сфераның диаметр бойындағы қарама-қарсы екі нүктесі, АВС және АDВ – ұштары А мен В нүктелерінде жататын жартылай шеңбер болсын, Г – осы шеңбердің бірігуі болсын.

Г фигура S\Г фигураны 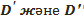екі бөлікке бөлетінін көрсетуге болады. 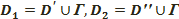фигуралардың әрқайсысы, төбелері А және В нүктелерінде жататын екібұрыш деп аталады. Берілген АВС және АDВ жартылай шеңберлері осы екібұрыштың қабырғалары деп аталады. Осы екіжақты бұрыштың сызықтық бұрышы берілген екібұрыштың бұрышы деп аталады. Егер екібұрыш тік болса, онда екібұрыш тік бұрышты деп аталады.

Q₁, Q₂ – әр түрлі екі үлкен шеңбер болсын, әрі 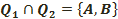делік. Біз мұнда П 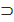Q₁ және Σ 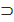Q₂ жазықтықтарды қиғаннан алынған вертикаль екіжақты бұрыштың екі қосағы мен S сферада ойып түсіретін вертикаль екібұрыштың екі қосағын табамыз. Егер осы екібұрыштың біреуі тек тік бұрышты болса, онда қалған үшеуі де тік бұрышты. Бұл жағдайда Q₁, Q₂ үлкен шеңберлер перпендикуляр деп аталады: Q₁ Q₂. Мынау түсінікті:

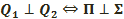
2. Екі А, В 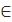S нүктесін алалық және Q осы нүктелерден өтетін үлкен шеңбер болсын. Q шеңбер, ұштары А және В нүктелерінде жататын өзінің 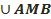және 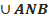екі доғасының бірігуі болып табылады. осы екі доғаның ұзындықтарының жартылай шеңберден ұзын емес, А және В нүктелерініңиарасындағы сфералық қашықтық деп аталады және d(А,В) деп белгіленеді. Демек d(А,В)≤πr, .

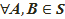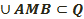жартылай шеңберден кем болсын, яғни d(А,В) – осы доғаның ұзындығы. АМВ доғаға сүйенетін АОВ цнтрлік бұрыштың шамасын α, ал АВ кесіндінің ұзындығы ρ(А,В) деп белгілелік. Мынау белгі:

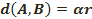(1)

АОВ үшбұрышынан мынаны табамыз:

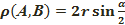(2)

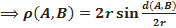(1), (2) (3)

3. Сфераның қозғалысы деп сол сфераның өзіне кез келген изометриялық бейнелеуін, яғни төмендегі шартты қанағаттандыратын f:S→S бейнелеуі аталады.

Егер F, 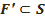екі фигураның біреуін екіншісіне көшіретін S сфераның қозғалысы бар болса, онда ол екі фигура конгурэнтті деп аталады.

4. S сферада жалпы жағдайдағы А, В, С үш нүктені алалық. Олар үш жартылай сфераны анықтайды, олардың әрқайсысы А, В, С нүктелерін қамтиды, оның үстіне, бұл нүктелердің екеуі жартылай сфераның шетінде жатады.

Осы үш жартылай сфераның қиылысуы төбелері А, В, С болатын сфералық үшбұрыш деп аталады. Үлкен шеңбердің АВ, ВС, АС доғалары (жартылай шеңберден кемдері) АВС сфералық үшбұрыштың қабырғалары деп аталады.

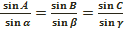немес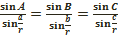

Бұл теңдіктер сфералыққ үшбұрыштарға сәйкес синустар теоремасын өрнектейді.

5. АВС сфералық үшбұрышты алалық. А^* деп Q(В,С) үлкен шеңбердің [Q(B,C), A] жартылай сферада жататын полюсін белгілелік. Дәл осы сияқты В^*, С^* нүктелерін табамыз.

А*, В^*, С^* сфералық үшбұрыш АВС сфералық үшбұрышқа қарағанда полрлық деп аталады.

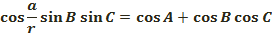
Бұл теңдік сфералық үшбұрышқа сәйкес косинустар теоремасын өрнектейді.

1.V – нақты сандардың R өрісі үстіндегі n+1 өлшемді евклидтік векторлық кеңістік болсын. Егер π:V\{0}→E бейнелеуі беріліп, ол мынадай:

1) π – сюръекция;

2) 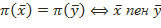коллинеар;

деген аксиомалары қанағаттандырса, онда Е≠ 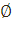жиыны Риманның n-өлшемді эллипстік кеңістігі деп аталады.

V векторлық кеңістік евклидтік болғандықтан, S_n кеңістігінде қашықтық ұғымын былай енгізуге болады. r оң санды береміз. Егер М₁, М₂ нүктелері векторларымен тудырылса, онда М₁, М₂ нүктелердің арасындағы қашықтық деп,

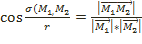(1)

шартты қанағаттандыратын теріс емес δ(М₁, М₂) санын айтамыз. r>0 саны S_n кеңістік қисықтығының радиусы деп аталады.

Сөйтіп, S_n эллипстік кеңістік Р_n проективтік кеңістік схемасымен салынады, бірақ тек V евклидтік векторлық кеңістіктің үстінде тұрғыз ылады және ондағы скаляр көбейтінді (1) формула бойынша S_n де қашықтықты анықтау үшін пайдаланылады.

(1)формуладан f кеңістіктің түрлендіруі оның кез келген нүктесінің арақашықтығын сақтайтыны шығады. Мұндай түрлендіру S_n кеңістіктің қозғалысы деп аталады.

2. n=2 жағдайын егжей-текжей қарастралық. S₂ қашықтық элиппстік жазықтық деп аталады.

Үш өлшемді Е₃ евклидтік кеңістікте О нүктесін таңдап алалық. Сонда, егер 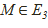нүктеге өзінің 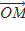радиус-векторына сәйкестендірсек, Е₃кеңістікті өзінің V көшірулер кеңістігімен пара-пар өтуге болатыны белгілі.

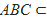S₂ үшбұрыштың ауданы мына формуламен есептеледі:

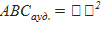
мұндағы ε=А+В+С-π – осы үшбұрыштың артығы.

Демек, кез келген 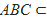S₂ үшбұрышта былай болады:

А+В+С>π.

3. S₂ эллипстік жазықтықтың проективтік моделін қарастыралық. S₂ жазықтық үш өлшемді эвклидтік V векторлық кеңістікпен тудырылған, ондағы векторлардың скаляр көбейтіндісі берілген 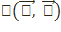бисызықтық форманың көмегімен анықталады.

Р₂=P(V) проективтік жазықтықта екінші ретті қисық Q анықталған: Ф(Х)=0, мұндағы Ф(Х)= 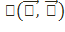, бұл 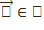векторы 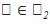нүктесін тудырған жағдайда болады. Бұл жағдайда V векторлық кеңістікте тек отогональ түрлендірулер, яғни векторлардың скаляр көбейтіндісін, демек, 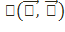квадраттық форманы сақтайтын V кеңістіктің сызықтық түрлендірулері қарастырылады. Демек, Р₂ жазықтықта біз кез келген проективтік түрлендірулерді емес, тек екінші ретті Q қисықтың Н Q стационар бөлімше (бөлгіш) группасын жасайтындарын қарастыруымыз керек.

V кеңістікте белгілі бір 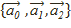ортонормальды базисті алалық. Ол Р₂ жазықтықтың 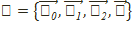проективтік реперін тудырады.Егер 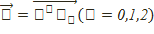болса, онда

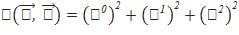
демек,R реперде Q қисық мына теңдеумен анықталады:

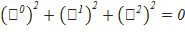
Бұдан Q-дің нольдік қисық екенін көреміз.

4. Біз эллипстік жазықтықтың екі моделін қарастырдық:

1) 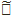жиыны Е₃ евклидтіккеңістіктегі радиусы r-ге тең Q сферасының қос диаметрлі қарам-қарсы нүктесі; қашықтық

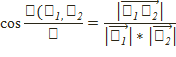
формула бойынша анықталады.

2) Q нольдік қисық (эллипстік жазықтықтың абсолюті) берілген Р₂ проективтік жазықтық және H_Q стационар бөлімше группадан алынған түрлендірулер ғана жіберіледі; қашықтық

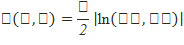
Формула бойынша анықталады.