Функція називається неперервною в точці , якщо для будь-якої послідовності відповідна послідовність значень збігається до

Функція 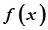називається неперервною в точці 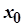,якщодля довільного числа 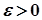існує число 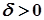таке, що для всіх 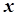, які задовольняють умову 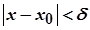, виконується нерівність .

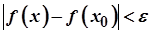Наведені означення рівносильні.

Функція 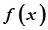називається неперервною в точці 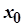справа (зліва), якщо .

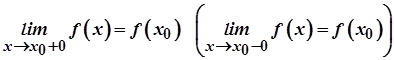Отже, функція 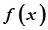неперервна в точці 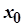, якщо вона неперервна в цій точці як справа, так і зліва.

Покажемо, що неперервна функція характеризується тим, що нескінченно малому приростові аргументу 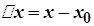відповідає нескінченно малий приріст функції .

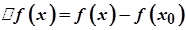Дійсно, умову 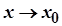можна записати як 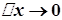. Тоді

.

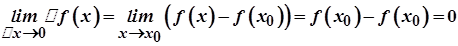Отже, можна дати наступне означення неперервності функції в точці 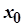. Функція 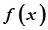називається неперервною в точці 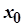, якщо нескінченно малому приростові аргументу в цій точці відповідає нескінченно малий приріст функції.

Уведене поняття неперервності функції є локальною (місцевою) властивістю. Якщо функція 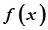неперервна в кожній точці інтервалу 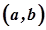, то говорять, що вона неперервна на інтервалі 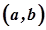. Якщо при цьому в точці 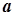функція неперервна справа, а в точці 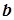– неперервна зліва, то говорять, що функція 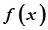неперервна на відрізку .

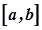Зауважимо, що термін неперервної кривої походить із поняття неперервної функції. Графіком неперервної на 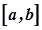функції є неперервна крива ("суцільна крива").

Операції над неперервними функціями

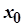Теорема. Якщо функції неперервні в точці , то функції 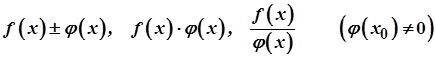у точці 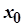також неперервні.

Доведення цієї теореми безпосередньо випливає з означення неперервності функції в точці та властивостей границь.

Теорема (про неперервність складеної функції). Якщо функція 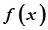неперервна в точці 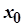, а функція 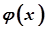неперервна в точці 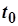, причому 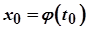, то складена функція 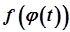неперервна, як функція від 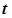, у точці .

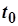Доведення. Нехай задано довільне число 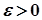. Тоді за неперервністю функції 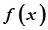у точці 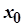знайдеться число 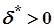таке, що 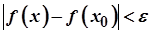для всіх 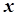, які задовольняють умову .

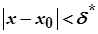Для числа 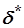за неперервністю функції 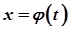у точці 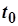знайдеться число 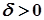таке, що для всіх 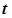, які задовольняють умову .

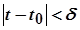Отже, для довільного числа 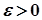знайдеться число 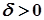таке, що з умови 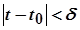випливає нерівність 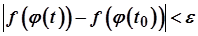, а це означає, що функція 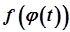неперервна в точці .

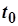Можна довести, що всі елементарні функції в області їх визначення неперервні.

Звернемо увагу на те, що з означення неперервності функції 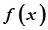у точці 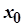випливає

.

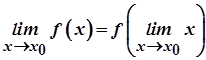Наведемо приклади деяких важливих границь, обчислення яких спирається на неперервність елементарних функцій.

1) .

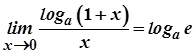Доведення.

.

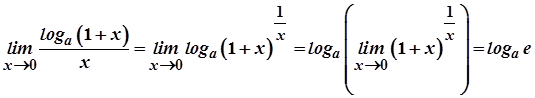Якщо 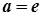, то маємо: 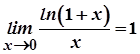, тобто при виконується .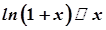

2) .

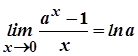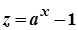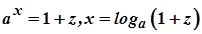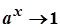Доведення. Покладемо . Тоді . Якщо , то і .

.

Якщо 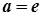, то маємо: 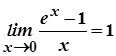, тобто при справедливо .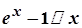

3) .

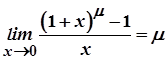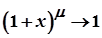Доведення. Покладемо . Якщо , то і .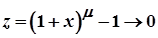

Далі 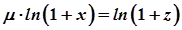. Звідси маємо: 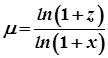. Тоді

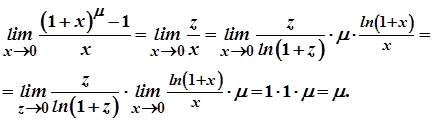
Розглянемо степенево-показниковий вираз 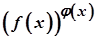. Нехай 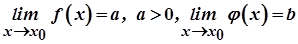. Запишемо

.

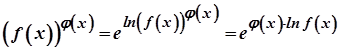Оскільки 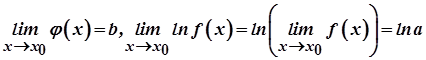, то 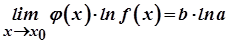. Звідси маємо

.

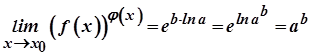Зазначимо, що вирази є не визначеними. Для знаходження відповіді на питання, що є границею виразу 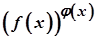, у цих випадках недостатньо знати лише границі функцій 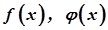, потрібно знати закон, за яким вони прямують до своїх границь.

3. Класифікація точок розриву функції.