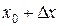Теорема. Якщо функція диференційовна в деякій точці, то у цій точці функція неперервна
Властивості
Якщо функція неперервна в кожній точці інтервалу (а,b), то вона називається
неперервною на цьому інтервалі.
Функція неперервна на відрізку [а,b], якщо вона неперервна на (а,b) і, крім того,
неперервна справа в точці а і зліва в точці b.
Сформулюємо теореми про неперервні функції.
Теорема 1(перша теорема Больцано-Коші). Якщо функція y = f (x)
неперервна на відрізку [а; b] і на його кінцях набирає значень різних знаків, то
всередині відрізка [а; b] знайдеться хоча б одна точка x = c , в якій функція
дорівнює нулю.
Теорема 2(друга теорема Больцано-Коші). Нехай функція y = f (x)
неперервна на відрізку [а; b] і набуває на його кінцях різних значень: f (a) =/ f (b) .
Тоді для довільного числа и є [ f (a); f (b)] знайдеться таке число c(a; b) , що
f (c) є и.
Теорема 3(Вейєрштрасса). Якщо функція y f (x) неперервна на відрізку
[а; b], то серед її значень на цьому відрізку існує найбільше і найменше.
8) Якщо хоча б одна з умов неперервності функції в точці не виконується, то
функція розривна в точці x0 , а саму точку x0 називають точкою розриву функції.
Класифікація точок розриву проводиться таким чином:
1) якщо існують лівостороння і правостороння границі функції в точці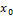 
, тобто 
,
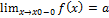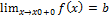, де a і b –скінченні числа, причому а не дорівнює b, то точку x0 називають точкою розриву першого роду; відмітимо, що в точці
x0 сама функція може бути як визначена так і невизначена;
2) якщо хоча б одна з границь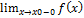 
, 
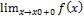не існує або дорівнює
нескінченості, то точку x0 називають точкою розриву другого роду, в точці x0
функція робить “нескінченний стрибок”
3) якщо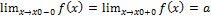 
, 
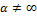, f(x0)≠a або в цій точці функція
невизначена, то точку x0 називають усувною точкою розриву
9) Похідною функції y = f(x) у точці Х називають число, до якого прямує відношення
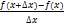Похідну функції f(x) позначають f'(x).
Фізичний зміст похідної. Якщо матеріальна точка рухається прямолінійно і її координата змінюється за законом S = S(t), то швидкість її руху v(t) у момент t дорівнює похідній S'(t): v(t) = S'(t)
Геометричний зміст похідної: значення похідної функції y = f(x) у точці x0 дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x0:
y' = f'(x0) = k = tgα.
Зв’язок між неперервністю і диференційовністю функції встановлює теорема.
Теорема. Якщо функція диференційовна в деякій точці, то у цій точці функція неперервна.
10) Основні правила диференціювання.
Теорема 1. Похідна сталої дорівнює нулю.
y = c,тоy΄ = 0
Теорема 2. Похідна алгебраїчної суми скінченого числа диференційованих функцій дорівнює алгебраїчній сумі похідних цих функцій
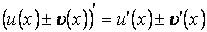
Теорема 3Похідна добутку двох диференційованих функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:
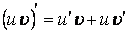
Теорема 4Сталий множник виносимо за знак похідної
(cu)΄ = cu΄,деc = const
Теорема 5Якщо чисельник і знаменник дробу диференційовані функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різниця добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат знаменника початкового дробу
11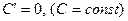 
; 
; 
; 
; 
;
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
.
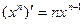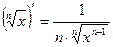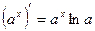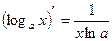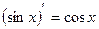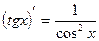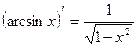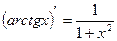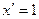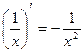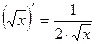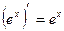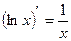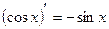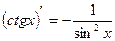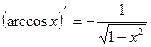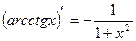12) Похідна складеної функції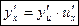 
Похідна оберненої функції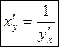 
Похіднафункції, заданої параметрично: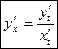 
Похідна неявно заданої функції
Якщо залежність між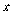 
та 
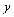задана в неявній формі 
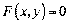, причому надалі будемо вважати, що 
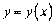диференційовна функція, то для знаходження похідної 
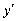достатньо:
а) знайти похідну по 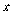від лівої частини рівняння, 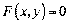, враховуючи, що 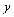є функцією ;
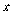б) прирівняти цю похідну до нуля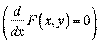 
в) розв’язати отримане рівняння відносно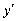
Логарифмічне диференціювання
Означення 1. Логарифмічною похідною функції називається похідна від логарифма цієї функції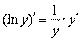 
.
Для знаходження похідної степенево-показникової функції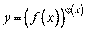 
має сенс застосовувати логарифмічне диференціювання.
Нехай 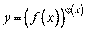. Якщо спочатку прологарифмувати за основою 
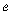обидві частини рівності: 
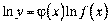, а потім продиференціювати, враховуючи, що 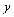є функцією 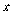, то отримаємо
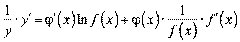
Звідки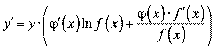 
або, якщо згадати вигляд 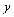, то
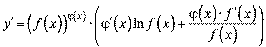
13)Якщо функція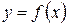 
має похідну 
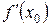в точці 
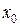, то вираз 
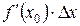називається диференціалом (differential) функції в цій точці і позначається символом 
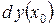. Тобто,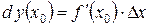 
Скористаємося геометричним змістом похідної: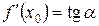 
.
З трикутника 
маємо: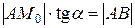 
або 
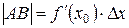. Але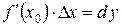 
, тому 
.
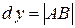Отже, диференціал функції 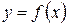в точці 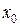визначає приріст ординати дотичної до кривої в точці 
при переході від абсциси 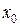до абсциси 