Вычислить криволинейный интеграл. где – контур прямоугольника с вершинами , , и .
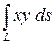
где  – контур прямоугольника с вершинами
– контур прямоугольника с вершинами 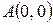 ,
, 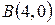 ,
, 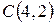 и
и  .
.
Вычислить криволинейный интеграл
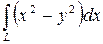
где  – дуга параболы
– дуга параболы 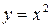 от точки
от точки 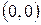 до точки
до точки 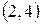 .
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 15
1. Вычислить интегралы:
1) 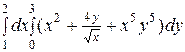
2) 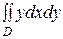 , где область
, где область  ограничена линиями:
ограничена линиями: 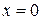 ,
, 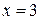 ,
, 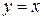 ,
, 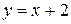 .
.
3) 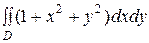 , где область
, где область  ограничена окружностью
ограничена окружностью 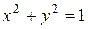 и
и
осями координат, и расположена в первой четверти.
2. Изменить порядок интегрирования в двойном интеграле:
1) 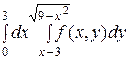 2)
2) 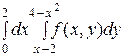
3. Вычислить площадь фигуры, ограниченной линиями: 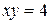 ,
, 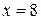 ,
, 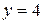 .
.
Вычислить криволинейный интеграл
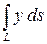
где  – дуга параболы
– дуга параболы 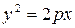 , отсечённая параболой
, отсечённая параболой 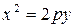 .
.
Вычислить криволинейный интеграл
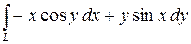
где  – отрезок, соединяющий точки
– отрезок, соединяющий точки 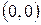 и
и 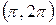 .
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 16
1. Вычислить интегралы:
1) 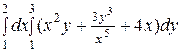
2) 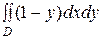 , где область
, где область  ограничена линиями:
ограничена линиями: 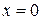 ,
, 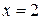 ,
, 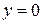 ,
, 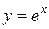 .
.
3) 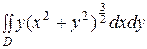 , где область
, где область 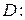
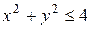 ,
, 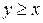 .
.
2. Изменить порядок интегрирования в двойном интеграле:
1) 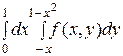 2)
2) 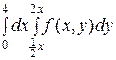
3. Вычислить площадь фигуры, ограниченной линиями:  ,
, 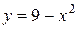 .
.
Вычислить криволинейный интеграл
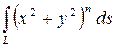
где  – окружность
– окружность 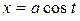 ,
, 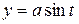 .
.
Вычислить криволинейный интеграл
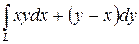
где  – линия
– линия  от точки
от точки 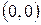 до точки
до точки 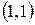 .
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 17
1. Вычислить интегралы:
1) 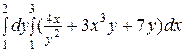
2) 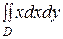 , где область
, где область  ограничена линиями:
ограничена линиями: 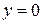 ,
, 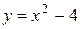 .
.
3) 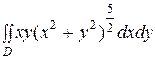 , где область
, где область  - кольцо
- кольцо 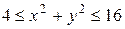 .
.
2. Изменить порядок интегрирования в двойном интеграле:
1) 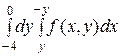 2)
2) 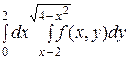
3. Вычислить площадь фигуры, ограниченной линиями: 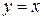 ,
, 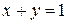 ,
, 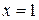 .
.
Вычислить криволинейный интеграл
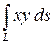
где  – четверть эллипса
– четверть эллипса 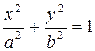 , лежащем в первом квадранте.
, лежащем в первом квадранте.
5. Вычислить криволинейный интеграл 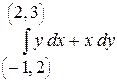
КОНТРОЛЬНАЯ РАБОТА
Вариант 18
1. Вычислить интегралы:
1) 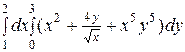
2) 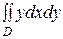 , где область
, где область  ограничена линиями:
ограничена линиями: 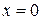 ,
, 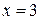 ,
, 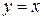 ,
, 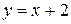 .
.
3) 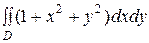 , где область
, где область  ограничена окружностью
ограничена окружностью 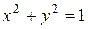 и
и
осями координат, и расположена в первой четверти.
2. Изменить порядок интегрирования в двойном интеграле:
1) 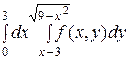 2)
2) 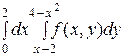
3. Вычислить площадь фигуры, ограниченной линиями: 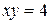 ,
, 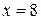 ,
, 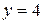 .
.
Вычислить криволинейный интеграл
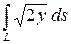
где  – первая арка циклоиды
– первая арка циклоиды 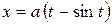 ,
, 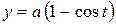 .
.
Вычислить криволинейный интеграл
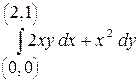
КОНТРОЛЬНАЯ РАБОТА
Вариант 19
1. Вычислить интегралы:
1) 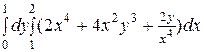
2) 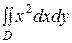 , где область
, где область  ограничена линиями:
ограничена линиями: 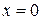 ,
, 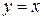 ,
, 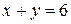 .
.
3) 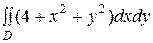 , где область
, где область  ограничена окружностью
ограничена окружностью 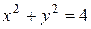 и
и
прямыми 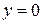 и
и 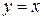 .
.
2. Изменить порядок интегрирования в двойном интеграле:
1) 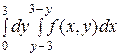 2)
2) 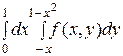
3. Вычислить площадь фигуры, ограниченной линиями: 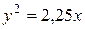 ,
, 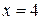 .
.
Вычислить криволинейный интеграл
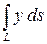
где  – дуга параболы
– дуга параболы 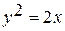 , отсечённая параболой
, отсечённая параболой 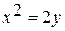 .
.
Вычислить криволинейный интеграл
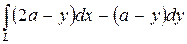
где  – первая от начала координат арка циклоиды
– первая от начала координат арка циклоиды 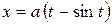 ,
, 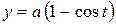 .
.
КОНТРОЛЬНАЯ РАБОТА
Вариант 20
1. Вычислить интегралы:
1) 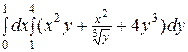
2) 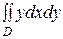 , где область
, где область  ограничена линиями:
ограничена линиями: 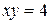 ,
, 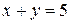 .
.
3) 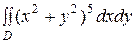 , где область
, где область  часть кольца между окружностями
часть кольца между окружностями 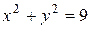 и
и 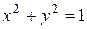 , расположенная во второй четверти.
, расположенная во второй четверти.
2. Изменить порядок интегрирования в двойном интеграле:
а) 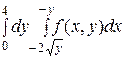 б)
б) 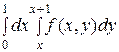
3. Вычислить площадь фигуры, ограниченной линиями: 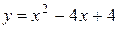 ,
, 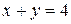 .
.
Вычислить криволинейный интеграл
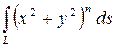
где  – окружность
– окружность 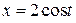 ,
, 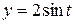 .
.
Вычислить криволинейный интеграл
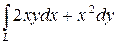
где  – линия
– линия 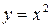 от точки
от точки 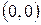 до точки
до точки 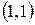 .
.
