Кореневі показники якості

Для непрямої оцінки якості управління використовують кореневі показники якості, які обумовлені розташуванням коренів p₁, p₂, … p_n... характеристичного рівняння замкнутої системи

а₀pⁿ + а₁p^n-1 + а₂p^n-2 +…+a_n=0

на комплексній площині.

Найбільш загальній кореневий показник якості – середнє геометричне значення модулів коренів (середньогеометричний корінь):

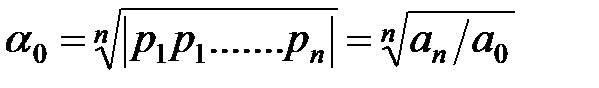
Середньогеометричний корінь 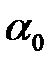визначає на дійсній осі комплексної площини 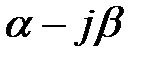точку, що є геометричним центром всіх корінь характеристичного рівняння. Величина 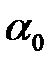має розмірність із^-1 і є узагальненою мірою швидкодії системи: чим менше 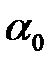, тим ближче корінь до мнимої осі й тем більше тривалість перехідного процесу.

Коефіцієнт a_n залежить від передатного коефіцієнта k розімкнутого контуру: для статичних систем a_n = 1+k, для астатичних a_n =k. Звідси можна зробити висновок: чим більше коефіцієнт k, тим краще швидкодія системи (за інших рівних умов – однакової конфігурації коренів).

Корені, розташовані ближче всього до мнимої осі називаються домінуючими, вони впливають на характер перехідного процесу й дають найбільш тривалі складові перехідного процесу.

Відстань від мнимої осі до найближчого до неї кореня називається ступенем стійкості η. Якщо найближчий корінь дійсний (корінь р₁), то домінуючою складовою перехідного процесу буде експонента з показником :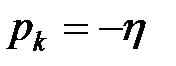

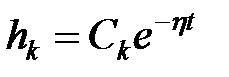
Якщо найближчими коренями до мнимої осі буде пара комплексно сполучених корінь, то домінуюча складовій перехідного процесу - коливальна складова, що загасає по експоненті.

В обох випадках тривалість перехідного процесу при припустимій погрішності регулювання d_п = 0,05С_к визначається за наближеною формулою: t_n £ 3/h, де знак «=» ставиться до випадку дійсного домінуючого кореня, а знак «<» - до випадку домінуючої комплексно сполученої пари коренів.

При виборі настроєних параметрів регулятора завжди прагнуть компенсувати домінуючі (найменші) корені, яким відповідають найбільші постійні часу об'єкта, і тим самим поліпшити швидкодію системи.

Коливальні властивості САУ визначає k-я пара комплексних корінь 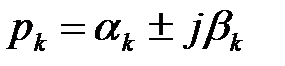для якої найбільше відношення

,

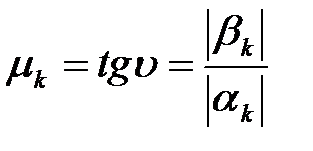або найбільший кут 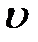між двома симетричними променями. У цьому випадку такою парою, що визначає домінуючу коливальну складовій перехідного процесу, є комплексні коріння р₁ і р₂.

Відношення 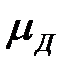мнимої частини b до дійсної частини a домінуючої пари комплексних корінь називають ступенем коливальності.

У практичних розрахунках найчастіше використовують кореневий показник коливальності:

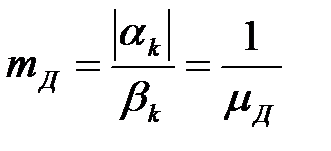
який також визначається через домінуючу пару комплексних корінь. При виборі налаштувань регулятора прагнуть отримати m_Д = 0,2 ¸ 0,5.

Спеціальними математичними дослідженнями встановлено, що в системі будь-якого порядку найбільш швидкий аперіодичний процес має місце, коли всі n коренів рівні між собою.

Максимальна швидкодія системи досягається при невеликий коливальності (d £ 10%). Для цього всі комплексні корені (і один дійсний при n непарному) повинні розташовуватися на однаковій відстані h від мнимої осі, а мнимі частини повинні утворювати арифметичну прогресію з різницею Db = b₁. Причому, для кожного порядку рівняння існує оптимальне відношення Db/h:

- для другого порядку Db/h = 1;

- для третього порядку Db/h = 1,45;

- для четвертого порядку Db/h = 0,79

- для п'ятого порядку Db/h = 1,5.

Визначення показників h і m по рівнянню з відомими коефіцієнтами є в загальному випадку такою же трудомісткою задачею, як і відшукання самих коренів. Легше вирішується зворотна задача – визначення коефіцієнтів рівняння й параметрів системи, при яких всіх корені лежать в області із заданим ступенем стійкості або заданим ступенем коливальності (рис.).

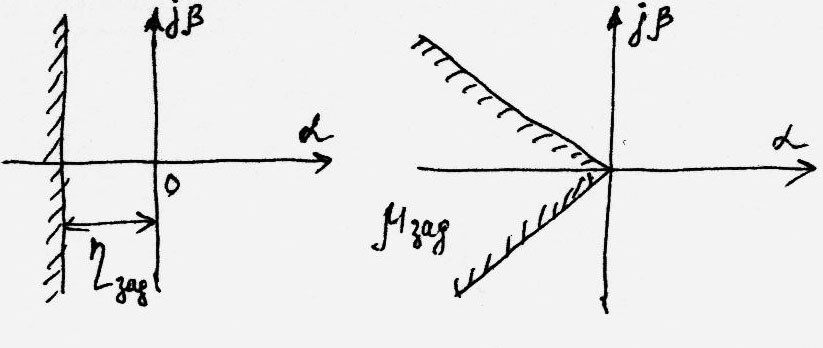
Для цього може бути використаний метод D-Розбивки. Тільки замість звичайної заміни 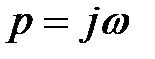в характеристичному рівнянні необхідно зробити підстановку 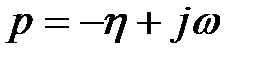або 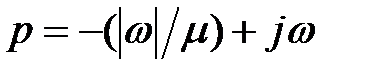, де h і m - задані числа. Виконуючи далі всі звичайні операції методу D-Розбивки, можна одержати області заданого ступеня стійкості й коливальності в просторі коефіцієнтів, що варіюються, і параметрів системи.

Кореневі показники a₀, h, m_Д, m_Д важливі для розуміння проблеми якості і її зв'язків із проблемою стійкості, але використовуються рідше інших, тому що їх безпосереднє визначення для конкретної системи високого порядку (n > 3) являє собою складне обчислювальне завдання.