Интерференция волн. Стоячие волны. Уравнение стоячей волны
Глава 7. Механические волны
Волны. Уравнение волны
Помимо уже рассмотренных нами движений, почти во всех областях физики встречается ещё один тип движения – волны. Отличительной особенностью этого движения, делающей его уникальным, является то, что в волне распространяются не сами частицы вещества, а изменения в их состоянии (возмущения).
Возмущения, распространяющиеся в пространстве с течением времени, называются волнами. Волны бывают механические и электромагнитные.
Упругие волны – это распространяющиеся возмущения упругой среды.
Возмущение упругой среды – это любое отклонение частиц этой среды от положения равновесия. Возмущения возникают в результате деформации среды в каком-либо её месте.
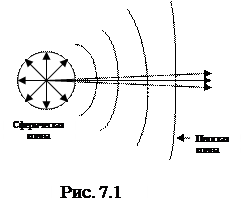
Совокупность всех точек, куда дошла волна в данный момент времени, образует поверхность, называемую фронтом волны.
По форме фронта волны делятся на сферические и плоские. Направление распространения фронта волны определяется перпендикуляром к фронту волны, называемым лучом. Для сферической волны лучи представляют собой радиально расходящийся пучок. Для плоской волны лучи- пучок параллельных прямых.
В любой механической волне одновременно существуют два вида движения: колебания частиц среды и распространения возмущения.
Волна, в которой колебания частиц среды и распространение возмущения происходят в одном направлении, называется продольной(рис.7.2 а).
Волна, в которой частицы среды колеблются перпендикулярно направлению распространения возмущений, называется поперечной(рис. 7.2 б).
В продольной волне возмущения представляют собой сжатие (или разрежение) среды, а в поперечной - смещения (сдвига) одних слоев среды относительно других. Продольные волны могут распространяться во всех средах (и в жидких, и в твёрдых, и в газообразных), а поперечные - только в твёрдых.
Каждая волна распространяется с некоторой скоростью. Под скоростью волны υ понимают скорость распространения возмущения. Скорость волны определяется свойствами среды, в которой эта волна распространяется. В твёрдых телах скорость продольных волн больше скорости поперечных.
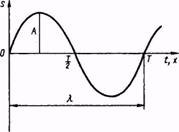
Длиной волны λ называется расстояние, на которое распространяется волна за время, равное периоду колебания в её источнике. Поскольку скорость волны – величина постоянная (для данной среды), то пройденной волной расстояние равно произведению скорости на время её распространения. Таким образом, длина волны
λ= υТ (7. 1)
Из уравнения (7.1) следует, что частицы, отделённые друг от друга интервалом λ, колеблются в одинаковой фазе. Тогда можно дать следующее определение длины волны: длина волны есть расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе.
Выведем уравнение плоской волны, позволяющее определить смещение любой точки волны в любой момент времени. Пусть волна распространяется вдоль луча от источника с некоторой скоростью υ.
Источник возбуждает простые гармонические колебания, и смещение любой точки волны в любой момент времени определяетcz уравнением
S = Asinωt (7. 2)
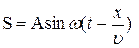
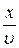Тогда точка среды, отстоящая от источника волны на расстоянии х, также будет совершать гармонические колебания, но с запаздыванием по времени на величину , т.е. на время, необходимое для распространения колебаний от источника до этой точки. Смещение колеблющейся точки относительно положения равновесия в любой момент времени будет описываться соотношением
(7. 3)
Это и есть уравнение плоской волны. Эта волна, характеризуется следующими параметрами:
· S — смещение от положения равновесии точки упругой среды, до которой дошло колебание;
· ω — циклическая частота колебаний, генерируемых источником, с которой колеблются и точки среды;
· υ — скорость распространения волны (фазовая скорость);
· х – расстояние до той точки среды, куда дошло колебание и смещение которой равно S;
· t – время отсчитываемое от начала колебаний;
Вводя в выражение (7. 3) длину волны λ, уравнение плоской волны можно записать так:
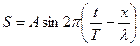(7. 4)
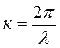или
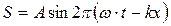(7. 5)
|
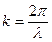называется волновым числом (число волн, приходящихся на единицу длины). Интерференция волн. Стоячие волны. Уравнение стоячей волны
Стоячие волны образуются в результате интерференции двух встречных плоских волн одинаковой частоты ω и амплитуды А.
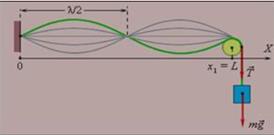Представим себе, что в точке S находится вибратор, от которого вдоль луча SO распространяется плоская волна. Достигнув преграды в точке О, волна отразится и пойдёт в обратном направлении, т.е. вдоль луча распространяются две бегущие плоские волны: прямая и обратная. Эти две волны когерентны, так как рождены одним и тем же источником и, накладываясь друг на друга, будут интерферировать между собой.
Возникающее в результате интерференции колебательное состояние среды и называется стоячей волной.
Запишем уравнение прямой и обратной бегущей волны:
прямая -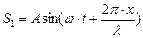 
; обратная -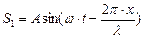 
где S1 и S2 – смещение произвольной точки на луче SO. С учётом формулы для синуса суммы результирующее смещение равно
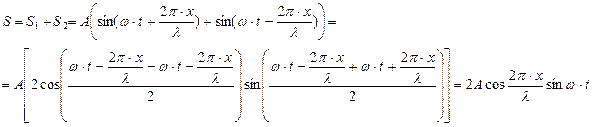
Таким образом, уравнение стоячей волны имеет вид
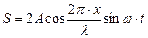
Множитель cosωt показывает, что все точки среды на луче SО совершают простые гармонические колебания с частотой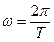 
. Выражение 
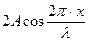называется амплитудой стоячей волны. Как видно, амплитуда определяется положением точки на луче SO (х).
Максимальное значение амплитуды будут иметь точки, для которых
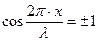или 
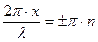(n = 0, 1, 2,….)
откуда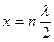 
, или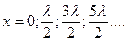 
(4.70)
Точки, имеющие такие координаты, называют пучностями стоячей волны.
Минимальное значение, равное нулю, будут иметь те точки для которых
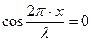или 
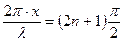(n = 0, 1, 2,….)
откуда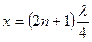 
или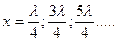 
(4.71)
Точки, имеющие такие координаты, называют узлами стоячей волны. Сопоставляя выражения (4.70) и (4.71), видим, что расстояние между соседними пучностями и соседними узлами равно λ/2.
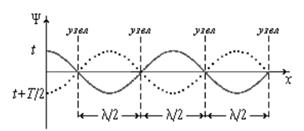На рисунке сплошной линией изображено смещение колеблющихся точек среды в некоторый момент времени, пунктирной кривой – положение этих же точек через Т/2. Каждая точка совершает колебания с амплитудой, определяемой её расстоянием от вибратора (х).
В отличие от бегущей волны в стоячей волне не происходит переноса энергии. Энергия просто переходит из потенциальной (при максимальном смещении точек среды от положения равновесия) в кинетическую (при прохождении точками положения равновесия)в пределах между узлами, остающимися неподвижными.
Все точки стоячей волны в пределах между узлами колеблются в одинаковой фазе, а по разные стороны от узла – в противофазе.
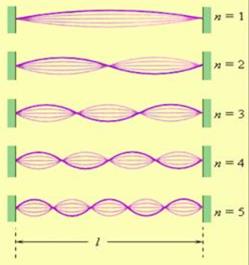
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.
Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.
Звук. Эффект Доплера
Продольные упругие волны, распространяющиеся в газе, жидкости и твёрдых телах, невидимы. Однако при определённых условиях их можно услышать. Так, если мы возбудим колебания длинной стальной линейки, зажатой в тисках, то порождаемые ею волны мы не услышим. Но если укоротить выступающую часть линейки и тем самым увеличить частоту её колебаний, то мы обнаружим, что линейка начнёт звучать.
Упругие волны, вызывающие у человека слуховые ощущения, называются звуковыми волнами или просто звуком.
Человеческое ухо способно воспринимать упругие механические волны с частотой ν от 16Гц до 20000Гц. Упругие волны с частотой ν<16Гц называют инфразвуком, а волны с частотой ν>20000Гц – ультразвуком.
Частоты в диапазоне от 16 Гц до 20000Гц называют звуковыми. Любое тело (твёрдое, жидкое или газообразное), колеблющееся со звуковой частотой, создаёт в окружающей среде звуковую волну.
В газах и жидкостях звуковые волны распространяются виде продольных волн сжатия и разряжения. Сжатия и разряжения среды, возникающее вследствие колебаний источника звука (струны, ножек камертона, голосовых связок и т.д.) , через некоторое время достигают человеческого уха и, заставляя барабанную перепонку уха совершать вынужденные колебания, вызывают у человека определённые слуховые ощущения.
В вакууме звуковые волны распространяться не могут, так как там нечему колебаться. В этом можно убедиться на простом опыте. Если поместить под стеклянный колпак воздушного насоса электрический звонок, то по мере выкачивания воздуха мы обнаружим, что звук будет становиться всё слабее, пока не прекратится совсем.
Звук в газах. Известно, что вовремя грозы мы сначала видим вспышку молнии и лишь, затем слышим раскаты грома. Это запаздывание возникает из-за того, что скорость звука в воздухе значительно меньше скорости света. Скорость звука в воздухе впервые измерил французский учёный Марен Мерсен в 1646 г. При температуре +20ºС она равна 343 м/с, т.е. 1235км/ч.
Скорость звука зависит от температуры среды. С увеличением температуры она возрастает, а с уменьшением убывает.
Скорость звука не зависит от плотности газа, в котором этот звук распространяется. Однако она зависит от массы его молекул. Чем больше масса молекул газа, тем меньше скорость звука в нём. Так, при температуре
0 ºС скорость звука в водороде 1284м/с, а в углекислом газе – 259 м/с.
Звук в жидкостях. Скорость звука в жидкостях, как правило, больше скорости звука в газах. Скорость звука в воде впервые была измерена в 1826г. Опыты проводились на Женевском озере в Швейцарии. На одной лодке поджигали порох и одновременно ударяли в колокол, опущенного в воду. Звук этого колокола с помощью специального рупора, также опущенного в воду, улавливался на другой лодке, которая находилась на расстоянии 14 км от первой. По разности времени между вспышкой света и приходом звукового сигнала определили скорость звука в воде. При температуре 8 ºС она оказалась равной 1435м/с.
В жидкостях скорость звука, как правило, уменьшается с ростом температуры. Вода является исключением из этого правила. В ней скорость звука увеличивается с ростом температуры и достигает максимума при температуре 74 ºС, а при дальнейшем увеличении температуры она уменьшается.
Нужно сказать, что человеческое ухо плохо «работает» под водой. Большая часть звука при этом отражается от барабанной перепонки и потому слуховых ощущений не вызывает. Именно это в своё время дало основание нашим предкам считать подводный мир «миром молчания». Отсюда же и выражение «нем как рыба». Однако ещё Леонардо да Винчи предлагал слушать подводные звуки, приложив ухо к веслу, опущенному в воду. Воспользовавшись таким способом, можно убедиться в том, что рыбы на самом деле довольно болтливы.
Звук в твёрдых телах. Скорость звука в твёрдых телах ещё больше, чем в жидкостях. Только здесь следует учитывать, что в твёрдых телах могут распространяться как продольные, так и поперечные волны. Скорость этих волн, как мы знаем, различна. Например, в стали поперечные волны распространяются со скоростью 3300м/с, а продольные –со скоростью 6100 м/с. В том, что скорость звука в твёрдом теле больше, чем в воздухе, можно убедится следующим образом. Если ваш товарищ ударит по одному концу рельсы, а вы приложите ухо к другому концу, то будут слышны два удара. Сначала звук достигнет вашего уха по рельсу, а затем – по воздуху.
Хорошей проводимостью обладает земля. Поэтому в старые времена при осаде в крепостных стенах помещали «слухачей», которые по звуку, передаваемому землёй, могли определить, ведёт ли враг подкоп к стенам или нет. Прикладывание уха к земле также позволяло обнаружить приближение вражеской конницы.
Помимо слышимых звуков, в земной коре распространяются и инфразвуковые волны, которые человеческое ухо уже не воспринимает. Такие волны могут возникать при землетрясениях.
Мощные инфразвуковые волны, распространяющиеся как в земле, так и в воздухе, возникают при извержении вулканов и взрывах атомных бомб. Источниками инфразвука могут служить и вихри воздуха в атмосфере, грузовые разряды, орудийные выстрелы, ветер, обтекающие гребни морских волн, работающие двигатели реактивных самолётов и т.д.
Ультразвук тоже не воспринимается человеческим ухом. Однако его способны излучать и улавливать некоторые животные, например летучие мыши и дельфины. В технике для получения ультразвука используют специальные устройства.