Свойства нормального распределения

Рассмотрим основные свойства этого важнейшего распределения.

Свойство 1. Функция плотности нормального распределения (21) определения на всей оси абсцисс.

Свойство 2. Функция плотности нормального распределения (21) больше нуля для любого из области определения ( ).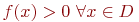

Свойство 3. При бесконечном увеличении (уменьшении) функция распределения (21) стремится к нулю .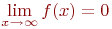

Свойство 4. При 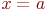функция распределения 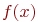, заданная (21), имеет наибольшее значение, равное

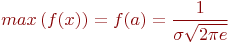(24)

Свойство 5. График функции 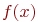(рис.9.11 ) симметричен относительно прямой .

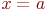Свойство 6. График функции 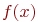(рис.9.11 ) имеет по две точки перегиба симметричные относительно прямой :

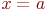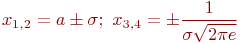(25)

Свойство 7. Все нечетные центральные моменты равны нулю. Заметим, что используя свойство 7, определяют асимметрию функции 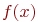по формуле 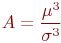. Если 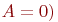, то делают вывод, что исследуемое распределение симметрично относительно прямой 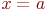. Если 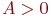, то говорят, что ряд смещен вправо (более пологая правая ветвь графика 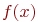или затянута). Если , тогда считают, что ряд смещен влево (более пологая левая ветвь графика рис.9.12 ).

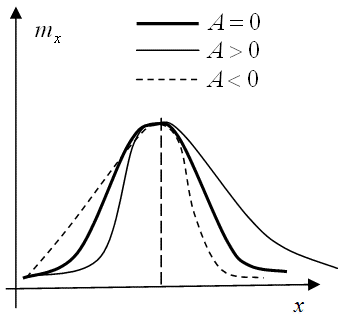
Рис. 9.12. Функция плотности распределения для различных А

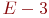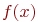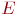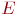Свойство 8. Эксцесс распределения равен 3. Часто на практике вычисляют и по близости этой величины к нулю определяют степень "сжатия" или "размытости" графика (рис.9.13 ). А так как связан с , то, в конечном итоге характеризует степень рассеяния частоты данных. А так как определяет точность измерений (степень рассеянности данных), то становится очевидным, почему в случае повышенной точности измерений, результаты будут группироваться около центра, а в результате кривая 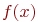будет круче подниматься в центре и резче спадать по мере удаления от среднего (рис.9.13 , 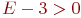). А тогда с увеличением , т.е. ухудшением качества измерений, рассеяние результатов увеличивается, а кривая 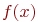принимает более пологий (сглаженный) вид (рис.9.13 , ).

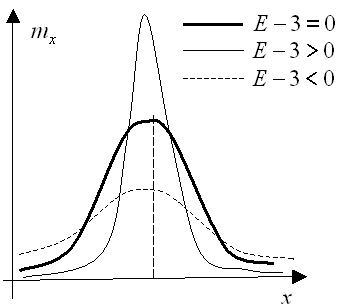
Рис. 9.13.

Свойство 9. Форма кривой 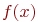не изменяется при изменении параметра .

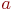График нормальной функции распределения (22) показан на рис.9.14 .

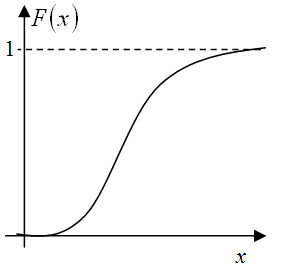
Рис. 9.14. График нормальной функции распределения

Правило трех сигм:

Площадь под кривой Гаусса в диапазоне

(Хср - Б; Xcp + Б) составляет 68,3%

(Хср - 2Б; Xcp + 2Б) составляет 95,4%

(Хср - 3Б; Xcp + 3Б) составляет 99,7%

Xcp - среднее. Б(сигма) - среднеквадратическое отклонение

Правило трёх сигм ( 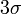) — практически все значения нормально распределённой случайной величины лежат в интервале 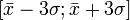. Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина 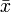истинная, а не полученная в результате обработки выборки).

Если же истинная величина 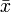неизвестна, то следует пользоваться не 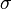, а s. Таким образом, правило трёх сигм преобразуется в правило трёх s