Оценивание параметров линейной модели множественной регрессии (ЛММР) при нормальном векторе случайных остатков методом максимального правдоподобия (ММП)

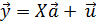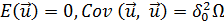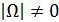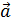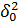Задача: пусть в схеме Гаусса-Маркова вектор случайных остатков с числовыми характеристиками , , имеет нормальный закон распределения. Требуется оценить параметры и модели методом максимального правдоподобия.

Решение: Будем предполагать, что объясняющие переменные в модели

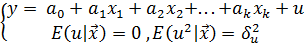
детерминированные, матрицу 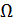полагаем известной. Из 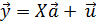и сделанного предположения о числовых характеристиках и законе распределения вектора 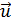следует, что вектор 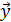тоже обладает нормальным законом распределения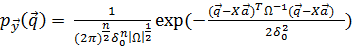

с числовыми характеристикам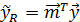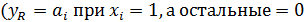и и .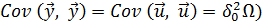

Для отыскания оценок параметров ММП действуем согласно следующему алгоритму:

1) составим функцию правдоподобия выборки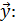

(

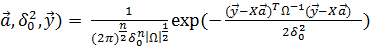
и вычисляем ее логарифм:

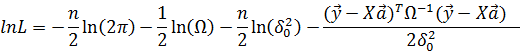
2) Найдем производные логарифма по аргументам и приравняем их к нулю:

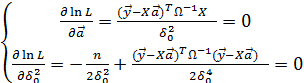
3) Решаем полученную систему уравнений. Сначала из первого уравнения ( после умножения его на 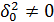) находим :

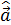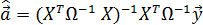
Затем подставляем его во второе уравнение системы и после умножения этого уравнения на 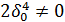находим 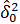= 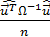, где 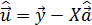. Полученные величины образуют решение системы и являются искомыми ММП-оценками параметров (эффективными и ассимптотически несмещенными).

Спецификация и оценивание нелинейных по коэффициентам моделей множественной регрессии со специальными функциями регрессии (на примере производственной модели с функцией Кобба-Дугласа).

Примером нелинейной по коэффициентам функции регрессии служит производственная функция Кобба-Дугласа:

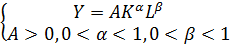(1)

В ней Y – уровень выпуска продукции за принятый отрезок времени; K и L – уровни соответственно основного капитала и живого труда, использованные в процессе выпуска величины Y. Подчеркнём, что функция не линейна по коэффициентам 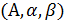. Это значит, что оценить параметры эконометрической модели с такой функцией регрессии строго нельзя ни одним из обсуждённых методов. Заметим, однако, что преобразование логарифмирования позволяет трансформировать функцию К-Д к линейной по коэффициентам:

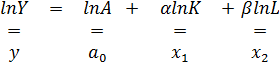(2)

Функция регрессии в уравнении (1) называется стандартной, поскольку операция логарифмирования трансформировала её к линейной по коэффициентам.

С учётом свойств операции логарифмирования составим следующим образом спецификацию модели товаров и услуг в стране:

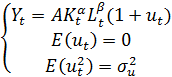(3)

(случайные возмущения включили в виде подходящего сомножителя)

После операции логарифмирования с учётом отмеченных в (2) обозначений, мы получили трансформацию модели (3) в виде базовой модели эконометрики:

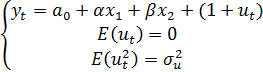
После оценивания линеаризованной модели можно вернуться при помощи операции возведения в степень к оценке исходной модели (3), где

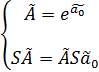
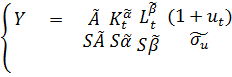
Оптимальное точечное прогнозирование значений эндогенной переменной по линейной модели (случай гомоскедастичного и неавтокоррелированного случайного остатка) на примере модели Оукена.

Рассмотрим построение оптимального (наиболее точного) прогноза искомого значения y₀ эндогенной переменной линейной модели множ. регрессии на примере модели Оукена:

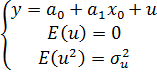, где

y – темп прироста реального ВВП, x₀=U_t-U_t-1 – изменение уровня безработицы.

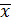₀ – значение экзогенной переменной, при которой должен быть вычислен прогноз величины y₀.

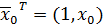
Прогноз величины y₀ обозначим символом .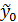

Мы предполагаем, что искомая величина и известные значения экзогенной переменной связаны м-ду собой уравнением линейной модели:

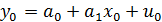
Прогноз 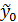будем строить так, чтобы оказались справедливыми следующие 2 требования к ошибкам прогноза:

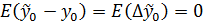– ожидаемая ошибка прогноза равна 0 (несмещённость прогноза)

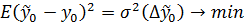– квадрат среднеквадратической ошибки прогноза минимален –кучность рассеивания минммальна(разброс минимален)

Справедлива следующая теорема – теорема об оптимальном прогнозе: Пусть справедливы все предпосылки теоремы Гаусса-Маркова для обучающей выборки . Тогда:

А) оптимальный прогноз величины y₀ вычисляется по формуле:

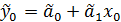(1)

Чтобы вычислить оптимальный прогноз, нужно оценить коэффициенты модели МНК и подставить в уравнение регрессии известное значение эндогенной переменной.

Б) Точность прогноза вычисляется по правилу:

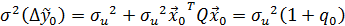, где

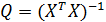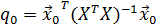, –квадратичная форма заданных значения экзогенной переменной, в случае модели Оукена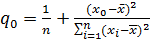

Неотрицательная константа q₀ отражает влияние на точность прогноза ошибок оценок коэффициентов модели-точность прогноза падает по мере удаления значения x₀ регрессора x от его выборочного среднего.

Среднеквадратичная ошибка прогноза (1) отыскивается по формуле: =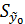

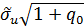
36. Тест Голдфелда-Квандта гомоскедастичности случайного остатка в ЛММР

Обратимся к предпосылке теоремы Гаусса-Маркова №2: Дисперсия случайного остатка не зависит от значений объясняющих переменных: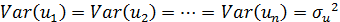

Обсудим тестирование этой предпосылки, записав её в виде следующей статистической гипотезы:

(*)

В основании процедуры проверки этой гипотезы лежит следствие из теоремы Гаусса-Маркова: при оценивании коэффициентов модели по двум группам уравнений наблюдений (в первую группу входят, например, n1 первых уравнений, во вторую – n2 последних уравнений наблюдений) следующая дробь:

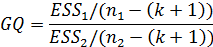
Эта дробь обладает законом распределения Фишера с количеством степеней свободы m1 =n1-(k+1) и m2= n2-(k+1).

Гипотеза Н0 может быть принята, если GQ не превосходит 2%-ой точки распределения Фишера.

Замечание: Гипотеза Н0 о гомоскедастичности остатка означает, что при любых перестановках наблюдений дисперсии случайных остатков остаются одинаковыми.

Обычное нарушение на практике возникает тогда, когда дисперсия случайного остатка возрастает (или убывает) с ростом абсолютных значений объясняющих переменных.

Тест Голдфелда-Квандта реализуется в итоге следующих шагов:

Шаг 1.Упорядочить уравнения наблюдений по возрастанию суммы модулей значений предопределенных переменных модели, т.е. по возрастанию значений .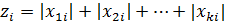

Замечание: В этот пункт процедуры Г-К заложена естественная предпосылка, что возможная гетероскедастичность случайного остатка в модели, т. е. зависимость его условной дисперсии 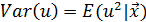от объясняющих переменных модели имеет специальный вид:

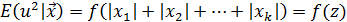, (1)

причём ф-ия f(z) является либо возрастающей, либо убывающей. Подчеркнём, что если случайный остаток гомоскедастичен, то любая зависимость 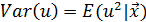от 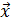, в частности зависимость (1) отсутствует.

Шаг 2. По первым n’ упорядоченным уравнениям наблюдений объекта (где n’ удовлетворяет условиям k+1<n’, n’≈0,3n, k+1 – кол-во оцениваемых коэффициентов ф-ии регрессии) вычислить МНК-оценки параметров модели и величину 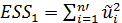, где 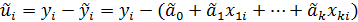– МНК-оценка случайного возмущения u_i.

Шаг 3. По первым n’ упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину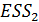

Шаг 4.Вычислить статистику

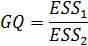
Шаг 5. Задаться уровнем значимости α и с помощью ф-ии FРАСПОБР при количествах степенней свободы 𝑣₁, 𝑣₂, где 𝑣₁= 𝑣₂=n’-(k+1), определить (1-α)-квантиль F_крит=F_1-α распределения Фишера.

Шаг 6. Принять гипотезу, если справедливы неравенства

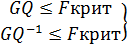, т. е. при этих справедливых неравенствах случайный остаток в модели полагать гомоскедастичным. В противном случае, гипотезу (*) отклонить как противоречащую реальным данным и делать вывод о гетероскедастичности случайного остатка в модели.

Тест корректен, когда остатки распределены по нормальному закону и выполнены другие предпосылки теоремы Г-М.

Обоснование: из-за утверждения выше 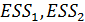– случайные переменные и распределены по закону хи-квадрат с количеством степеней свободы n’-(k+1), кроме того они независимы. А значит, 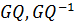- случайные переменные и распределены по Фишеру с количеством степеней свободы 𝑣₁, 𝑣₂. Следовательно критерием нулевой гипотезы может служить множество: 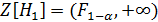. А если величина 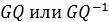попадает в это множество, то гипотезу следует отклонить в пользу альтернативной гипотезы 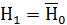, представляющей отрицание гипотезы (*), т. е. означающей гомоскедастичность случайного остатка в модели.