Свойства функции распределения

Функция распределения 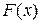является исчерпывающей вероятностной характеристикой случайной величины, поскольку позволяет определять вероятности любых событий с ней связанных. Это вытекает из следующих ее свойств функции распределения.

F0). 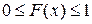для любого .

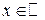(свойство следует из определения, так как 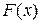- вероятность).

F1). Функция распределения 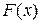является функцией неубывающей: .

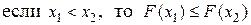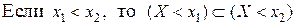▲ . Поэтому в силу свойства 3 вероятности ■.

F2). .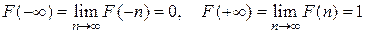

▲ Нестрогое доказательство данного свойства и его смысл состоят в следующем:

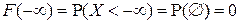в силу свойства 2 вероятности;

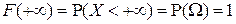в силу аксиомы нормированности Р2).

Строгое доказательство свойства F2) основано на использовании аксиомы непрерывности Р4).

Рассмотрим события 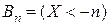, 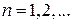. Нетрудно заметить, что последовательность событий 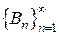удовлетворяет свойствам: 1) ;
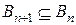2) 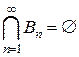. Поэтому в силу аксиомы непрерывности

.

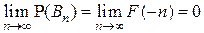Свойствам аксиомы непрерывности удовлетворяют также события 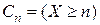, 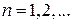и поэтому 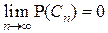. Поскольку 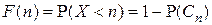, то ■.

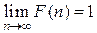F3). Функция распределения 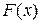является функцией непрерывной слева, то есть для любого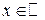

,

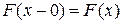где 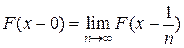- предел слева функции распределения в точке х.

▲ Рассмотрим события 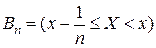, 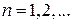. В силу аксиомы непрерывности 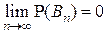. Поскольку

,

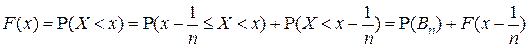то ■.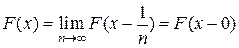

Замечание. Отметим, что если функцию распределения определить как 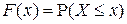, то она будет функцией непрерывной справа.

Замечание. Свойства F1), F2) и F3) полностью описывают класс функций распределения в смысле следующего утверждения (без доказательства).

Если функция 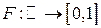удовлетворяет свойствам F1), F2) и F3), то 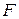есть функция распределения некоторой случайной величины 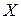, то есть найдется вероятностное пространство 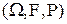и такая случайная величина на этом пространстве, что .

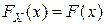F4). Для любого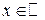

,

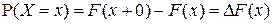где 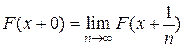- предел справа функции распределения в точке х, 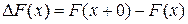- величина скачка функции распределения в точке .

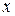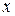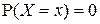Следствие. Если функция распределения непрерывна в точке , то . Если функция распределения непрерывна для любог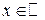о , то 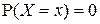для любого .

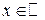▲ Поскольку справедливо представление

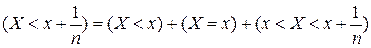
и события в сумме являются попарно несовместными, то в силу аддитивности вероятности

.

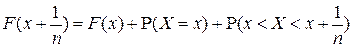Доказательство свойства следует из того, что последовательность событий 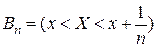, 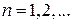удовлетворяет аксиоме непрерывности и поэтому ■.

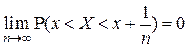F5). Для любого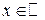

.

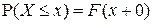▲ Действительно,

■.

Замечание. Геометрически свойства F3), F4) и F5) означают следующее. В точках 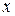, где функция распределения имеет разрыв 1 рода, то есть когда 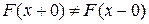, за значение функции распределения принимается левое (нижнее, меньшее). При этом вероятность события 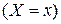является ненулевой и ее значение равно величине скачка 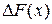. В точках непрерывности функции распределения свойства F3) F4) и F5) содержательными не являются.

F6). Вероятность попадания случайной величины 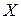в интервал 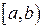определяется как приращение функции распределения на этом интервале:

для любых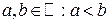

.

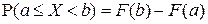▲ Поскольку 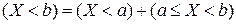и события в сумме являются несовместными, то в силу аддитивности вероятности

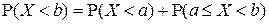
или, что эквивалентно,

■.

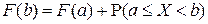F7). .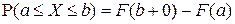

F8). .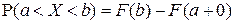

F9). .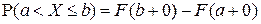

(Доказать свойства F7), F8) и F9) самостоятельно).

В общем случае график функции распределения может иметь вид:

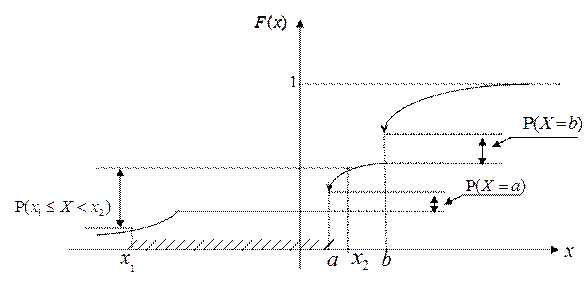
В приложениях, как правило, встречаются случайные величины, функции распределения которых являются либо везде кусочно-постоянными (дискретные случайные величины), либо везде непрерывными и даже гладкими (непрерывные случайные величины). В каждом из этих случаев существуют более удобные, чем функция распределения, вероятностные характеристики случайных величин.

2.2. Дискретные случайные величины. Закон распределения дискретной случайной величины.

Определение. Случайная величина 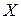, заданная на вероятностном пространстве 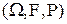, называется дискретной, если множество ее возможных значений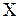конечно или счетно:

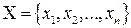или .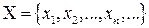

Для полной вероятностной характеристики дискретной случайной величины 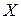достаточно указать все ее возможное значения 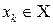и вероятности 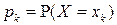, с которыми эти значения принимаются, 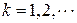. При этом, поскольку события 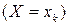, , 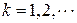образуют полную группу событий, то

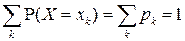(условие нормировки).

Подобную информацию о дискретной случайной величине записывают в виде таблицы:

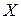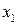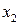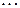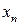						(2.1)

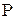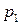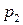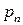которую называют законом распределения дискретной случайной величины 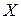или рядом распределения.

Закон распределения (2.1) является более удобной и наглядной вероятностной характеристикой, чем функция распределения, и его задание полностью эквивалентно заданию функции распределения.

Действительно, функция распределения дискретной случайной величины определяется по закону распределения (2.1) с помощью формулы:

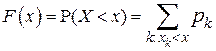. (2.2)

Подробнее в случае конечного числа значений дискретной случайной величины формула (2.2) выглядит следующим образом:

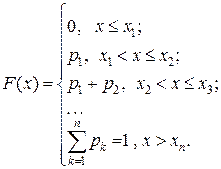
График функции распределения дискретной случайной величины является кусочно-постоянным со скачками в точках 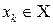равными 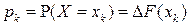, . Это означает, что закон распределения (2.1) по функции распределения (2.2) всегда можно однозначно восстановить.

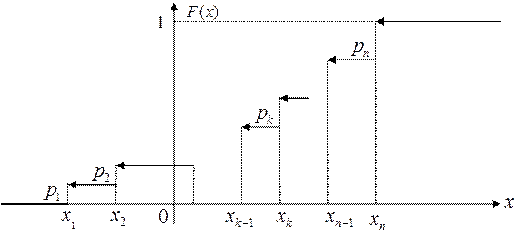
Вероятность попадания дискретной случайной величины 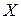в любое борелевское множество на числовой прямой 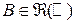определяется по формуле:

.

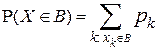Отметим, что через функцию распределения вероятность 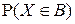в явном виде может и не выражаться.

2.3. Важнейшие дискретные случайные величины

и их законы распределения

1. Вырожденная случайная величина.

Любую константу С можно рассматривать как случайную величину, принимающую одно значение: 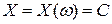для любого .

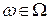Закон распределения вырожденной случайной величины имеет вид:

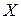	С

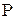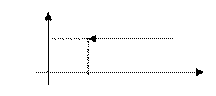
Выражение для функции распределения вырожденной случайной величины и ее график также имеют вырожденный вид:

F(x)

x

С

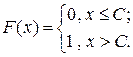
2. Индикаторная случайная величина.

С любым случайным событием А можно связать случайную величину вида:

.

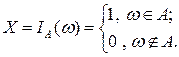Случайная величина 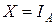называется индикатором случайного события А или индикаторной случайной величиной. Она принимает только два значения 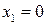и 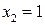, при этом

, .

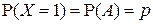Закон распределения индикаторной случайной величины имеет вид:

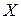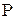	q	p

Аналитическое выражение и график функции распределения имеют вид:

x

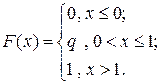
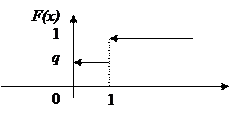
3. Биномиальная случайная величина.

Биномиальной называется дискретная случайная величина 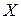, представляющая собой число успехов в n независимых испытаниях, проводимых по схеме Бернулли, с вероятностью успеха в одном испытании равной р.

Множество возможных значений биномиальной случайной величины:

.

Вероятности, с которыми значения принимаются, определяются по формуле Бернулли:

.

Закон распределения имеет вид:

				n

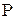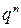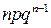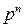и называется биномиальным законом распределения.

Условие нормировки при этом следует из формулы Бернулли или непосредственно из бинома Ньютона:

.

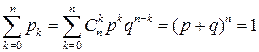(Записать аналитическое выражение для функции распределения и построить ее график самостоятельно).

Сокращенное обозначение для биномиальной случайной величины:

.

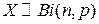4. Геометрическая случайная величина.

Геометрической называется дискретная случайная величина 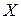, представляющая собой число испытаний, проводимых по схеме Бернулли, до появления первого успеха с вероятностью успеха в одном испытании равной р.

Геометрическая случайная величина имеет счетное множество возможных значений:

.

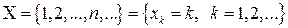Вероятности значений определяются по формуле:

.

Закон распределения имеет вид:

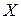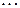				n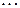

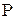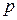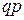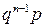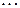и называется геометрическим законом распределения.

Условие нормировки при этом следует из формулы для суммы бесконечно убывающей геометрической прогрессии:

.

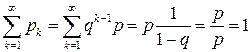(Записать аналитическое выражение для функции распределения и построить ее график самостоятельно).

Сокращенное обозначение для геометрической случайной величины:

.

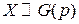5. Пуассоновская случайная величина.

Пуассоновской называется целочисленная случайная величина, множество возможных значений которой

,

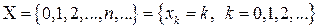а вероятности, с которыми значения принимаются, задаются формулой:

.

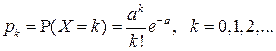Число 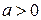называется параметром пуассоновской случайной величины.

Закон распределения имеет вид:

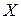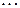				n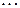

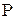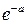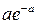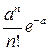и называется пуассоновским законом распределения.

Условие нормировки при этом следует из разложения экспоненты в ряд Тейлора:

.

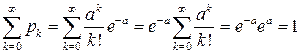(Записать аналитическое выражение для функции распределения и построить ее график самостоятельно).

Сокращенное обозначение для пуассоновской случайной величины:

.

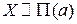2.4. Непрерывные случайные величины.

Плотность вероятностей

Определение. Случайная величина 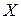, заданная на вероятностном пространстве 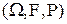, называется непрерывной или имеющей непрерывный закон распределения, если существует такая функция 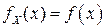, что для любого 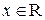функция распределения случайной величины 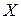допускает представление:

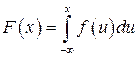. (2.3)

При этом функция 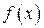называется плотностью вероятностей (плотностью распределения вероятностей, плотностью распределения) случайной величины .

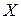Замечание. Для существования интеграла (2.3) предполагается, что плотность вероятностей 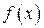является функцией непрерывна всюду, за исключением, может быть, конечного числа точек.

Из определения следует:

1. Если случайная величина 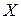является непрерывной, то ее функция распределения непрерывна на всей числовой прямой.

(Это следует из свойств интеграла с переменным верхним пределом).

Следствие. Если случайная величина 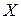является непрерывной, то

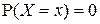для любого 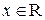. (2.4)

2. Если случайная величина 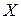является непрерывной, то ее функция распределения является дифференцируемой во всех точках, где плотность вероятностей 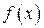непрерывна, и при этом справедливо равенство:

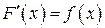. (2.5)

(Этот факт также следует из свойств интеграла с переменным верхним пределом).

В точках, где плотность вероятностей 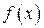непрерывной не является, производная функции распределения 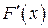не существует. Это означает, что в этих точках функция распределения , являясь функцией непрерывной, имеет излом, так что 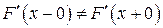. Но таких точек в соответствии с замечанием не более конечного числа и в них плотность вероятностей может быть задана произвольно (на величине интеграла (2.3) и на вероятностях событий, связанных со случайной величиной, в соответствии с (2.4) это никак не отражается).

Замечание. Говорят также, что равенство (2.5) выполняется «почти всюду» или «для почти всех 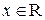», понимая под этим справедливость равенства «везде» или «для всех 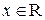», кроме (возможно) 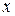из некоторого множества нулевой меры (длины). Используя данную терминологию, можно сказать, что функция распределения непрерывной случайной величины является дифференцируемой почти всюду.

Геометрическая иллюстрация.

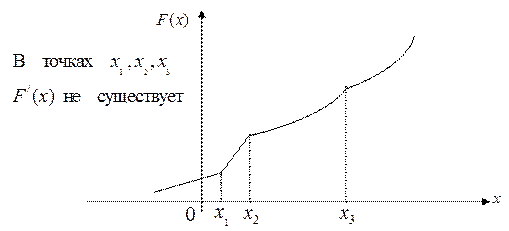
Из равенства (2.5) и определения производной следует, что

.

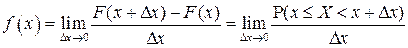Интерпретируя вероятность 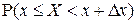как массу, приходящуюся на интервал 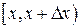, отношение 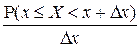представляет собой среднюю плотность массы на этом интервале, а в пределе при 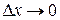получаем плотность массы в точке х. Это обстоятельство и оправдывает использование термина «плотность» для функции .

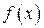Формулы (2.3) и (2.5) показывают, что между функцией распределения непрерывной случайной величины и плотностью вероятностей 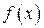существует взаимно однозначное соответствие. Поэтому по аналогии с дискретным случаем плотность вероятностей можно называть законом распределения непрерывной случайной величины или непрерывным законом распределения.