Описание поведения системы
Описание динамики системы составляет основу любой имитационной модели (ИМ).
6.3.1. Общие положения.
Случайные факторы в зависимости от их природы могут быть отражены в модели как:
- случайные события (например, отказ);
- случайные величины (интервал времени);
случайные функции.
В основе всех методов и приемов моделирования случайных факторов лежит использование случайных чисел, имеющих равномерное распределение на интервале либо [0; 1], либо [-1; 1].
“Истинно” случайные числа формируются с помощью АЦП на основе сигналов физических генераторов, использующих естественные источники случайных шумов.
Случайные числа, генерируемые аппаратно или на ЭВМ, называются псевдослучайными. (Но их статистические свойства совпадают со статистическими свойствами “истинно” случайных чисел).
В составе всех (практически) современных систем программирования входят специальные функции генерации случайных чисел, которые обычно называют датчиками или генераторами случайных чисел.
6.3.2. Методика моделирования случайных факторов
Наиболее простой метод программной генерации случайных чисел – это мультипликативный. В его основе лежит следующее рекуррентное соотношение:
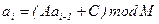 , (6.1)
, (6.1)
где 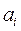 ,
, 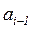 - очередное и предыдущее случайные числа;
- очередное и предыдущее случайные числа;
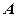 ,
, 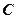 - константы;
- константы;
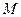 - достаточно большое целое положительное число (чем больше
- достаточно большое целое положительное число (чем больше 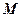 , тем длиннее неповторяемая последовательность).
, тем длиннее неповторяемая последовательность).
Достоинством этого метода является то, что при одних и тех же значениях, входящих в выражение (6.1) величин можно полностью воспроизвести эксперименты.
На практике часто используют удобное и наглядное выражение, по которому определяют случайное значение какого – либо параметра, входящего в имитационную модель:
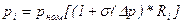 , (6.2)
, (6.2)
где 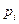 - случайное значение параметра;
- случайное значение параметра;
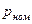 - его номинальное значение;
- его номинальное значение;
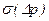 - среднеквадратическое отклонение значений параметра относительно его номинального значения;
- среднеквадратическое отклонение значений параметра относительно его номинального значения;
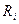 - значения случайных чисел, имеющих заданное (равномерное, нормальное и др.) распределение на интервале [-1; 1].
- значения случайных чисел, имеющих заданное (равномерное, нормальное и др.) распределение на интервале [-1; 1].
6.3.3. Два подхода к моделированию случайных чисел
Условно можно выделить два подхода к получению случайных чисел: аналитический и графический [21].
Аналитический способ
Для получения случайных значений параметра P аналитическимспособом можно использовать зависимости, представленные в таблице 6.1.
Таблица6.1 Аналитические зависимости для формирования случайных величин
| Закон распределения случайной величины P | Аналитическое выражение зависимости | Обозначения |
Равномерный в интервале изменения 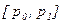 с плотностью с плотностью  | 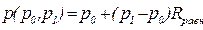 | 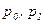 - границы интервала изменения величины P; - границы интервала изменения величины P; 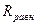 - случайная величина, равномерно распределенная в интервале - случайная величина, равномерно распределенная в интервале 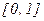 |
Нормальный с плотностью 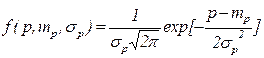 | 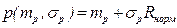 | 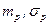 - математическое ожидание и СКО величины P; - математическое ожидание и СКО величины P; 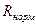 - случайная величина из нормально распределенной совокупности с математическим ожиданием - случайная величина из нормально распределенной совокупности с математическим ожиданием 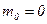 и СКО и СКО 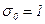 |
Экспоненциальный с плотностью 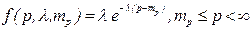 | 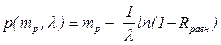 | 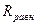 - случайная величина, равномерно распределенная в интервале - случайная величина, равномерно распределенная в интервале 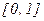 ; ; 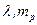 - параметры распределения - параметры распределения |
Для получения случайных величин, имеющих другие распределения, существуют специальные методики.
Например, в [21] для этого используются нормированные случайные величины, распределенные по нормальному или равномерному законам.
Графический способ
Методика получения случайных величин графическим способом заключается в следующем.
По этой методике, называемом преобразованием равномерно распределенной случайной величины, используется тот факт, что интегральная функция распределения любой непрерывной случайной величины равномерно распределена в интервале 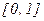 , т.е. для любой случайной величины pс плотностью распределения
, т.е. для любой случайной величины pс плотностью распределения 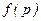 случайная величина
случайная величина
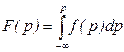 (6.1)
(6.1)
имеет равномерное распределение в интервале 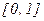 , или функции
, или функции 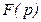 соответствует плотность распределения
соответствует плотность распределения
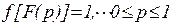 . (6.2)
. (6.2)
 |
Эта методика может быть проиллюстрирована рисунком 6.1
