Метод областей 5 страница
в) Графиком функции 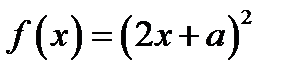 является парабола с подвижной вершиной в точке (– 0,5а; 0), где
является парабола с подвижной вершиной в точке (– 0,5а; 0), где 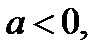 ветви которой направлены вверх.
ветви которой направлены вверх.
5. Из рисунка 24 (масштаб на осях координат разный) следует, что исходное уравнение имеет три корня при тех значения параметра  , при которых парабола
, при которых парабола 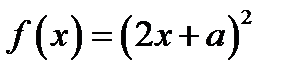 проходит через точку (8; 36) при условии, что
проходит через точку (8; 36) при условии, что 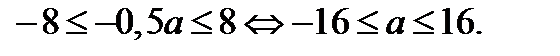
Парабола 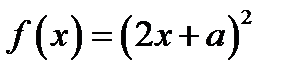 проходит через точку (8; 36), если
проходит через точку (8; 36), если
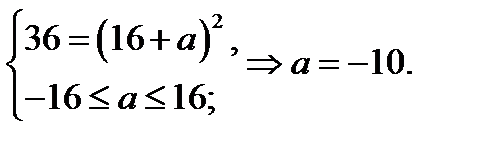
Из замечания следует, что исходное уравнение и при 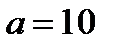 имеет три корня.
имеет три корня.
Ответ. 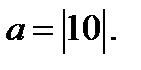
23.Найдите все значения параметра а, при каждом из которых уравнение 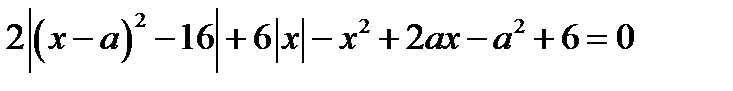 имеет единственный корень.
имеет единственный корень.
Решение. 1. Если 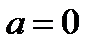 , то исходное уравнение принимает вид
, то исходное уравнение принимает вид 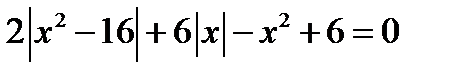 . (23.1)
. (23.1)
Уравнение (23.1) имеет нечётное число корней тогда и только тогда, когда 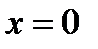 является корнем уравнения (так как
является корнем уравнения (так как 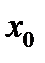 и
и  являются одновременно корнем уравнения). Легко проверить, что
являются одновременно корнем уравнения). Легко проверить, что 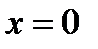 не является корнями уравнения (23.1), поэтому при
не является корнями уравнения (23.1), поэтому при 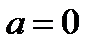 исходное уравнение не может единственного корня.
исходное уравнение не может единственного корня.
2. Исходное уравнение равносильно уравнению
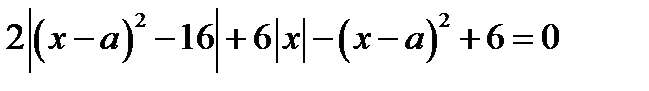 .
.
Сделаем замену 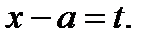 Тогда
Тогда 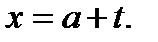 Исходное уравнение принимает вид
Исходное уравнение принимает вид 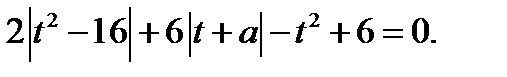 (23.2)
(23.2)
Исходное уравнение и уравнение (23.2) имеют одинаковое число решений при одних и тех же значениях параметра а (так как 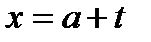 , то для каждого значения t находится единственное значение х).
, то для каждого значения t находится единственное значение х).
Перепишем уравнение (23.2) в виде 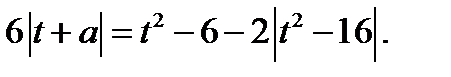 Так как
Так как 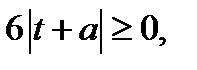 то уравнение (23.2), имеет решение, если
то уравнение (23.2), имеет решение, если
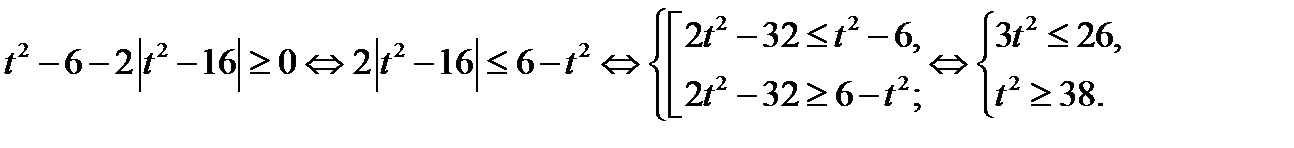
Из последней системы следует, что уравнение (23.2), имеет решение, если 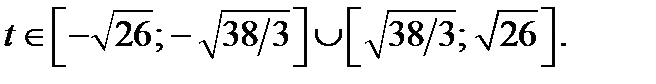
Замечание.Если точка 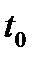 является корнем уравнения (23.2) при
является корнем уравнения (23.2) при 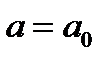 ,то
,то 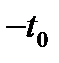 является корнем этого уравнения при
является корнем этого уравнения при 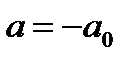 . Это следует из того, что
. Это следует из того, что 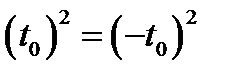 и
и 
Из замечания следует: еслиуравнение (23.2), а значит и исходное уравнение, имеет один корень при 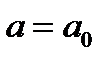 , то оно имеет также один корень при
, то оно имеет также один корень при 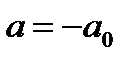 .
.
Рассмотрим исходное уравнение при 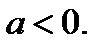 Имеем
Имеем
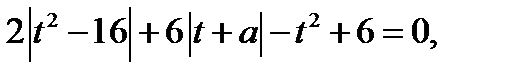 где
где 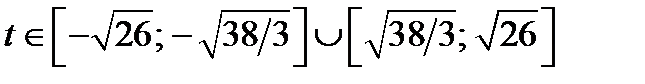 и
и 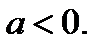 (23.3)
(23.3)
Уравнение (23.3) равносильно совокупности
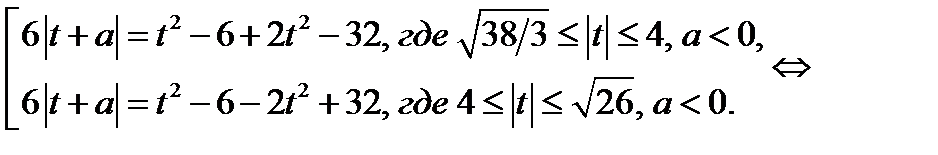
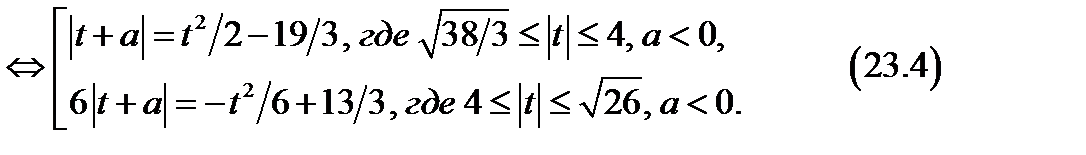
2. На плоскости 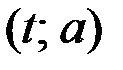 при
при 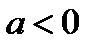 построим множество точек, удовлетворяющих совокупности (23.4).
построим множество точек, удовлетворяющих совокупности (23.4).
Для построения множества точек проделаем следующее.
Приравняем нулю выражение, стоящие под знаком модуля 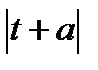 ,
,
где 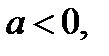 и получим уравнение
и получим уравнение 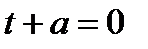 . Построим прямую
. Построим прямую 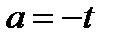 . Эта
. Эта
прямая разобьют плоскость 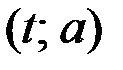 на 2 области. В области I выполняется неравенство
на 2 области. В области I выполняется неравенство 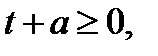 где
где 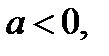 а в области II –
а в области II – 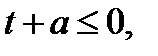 где
где 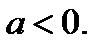
Рассмотрим совокупность (23.4) в каждой области.
1) В области I совокупность (23.4) равносильна совокупности
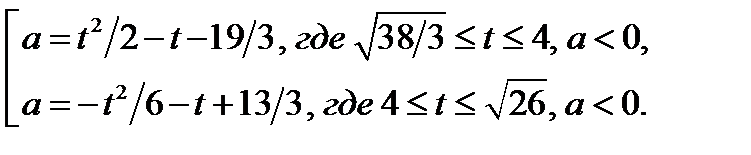
а) Если 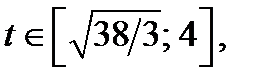 то
то 
Графиком функции 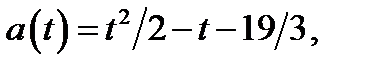 где
где 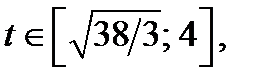 является часть параболы. Так как абсцисса вершины параболы
является часть параболы. Так как абсцисса вершины параболы 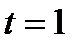 не принадлежит отрезку
не принадлежит отрезку 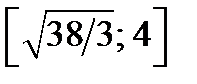 и ветви параболы направлены вверх, то на этом отрезке функция
и ветви параболы направлены вверх, то на этом отрезке функция 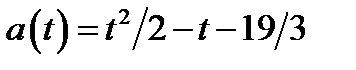 возрастает. Поэтому для построения части параболы найдём следующие значения функции
возрастает. Поэтому для построения части параболы найдём следующие значения функции 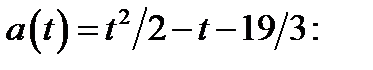
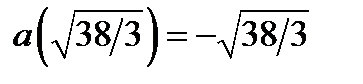 ,
, 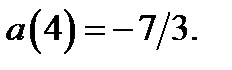
Отметим: точки 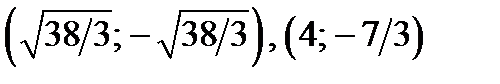 принадлежат области I.
принадлежат области I.
Строим часть параболы 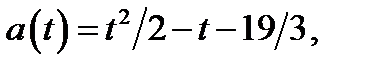 где
где 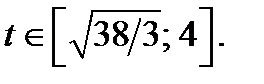
б) Если 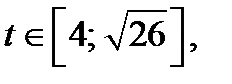 то
то 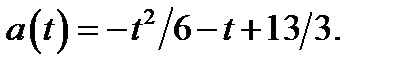
Графиком функции  где
где 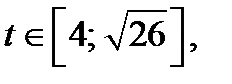 является часть параболы. Так как абсцисса вершины параболы
является часть параболы. Так как абсцисса вершины параболы 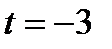 не принадлежит отрезку
не принадлежит отрезку 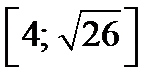 и ветви параболы направлены вниз, то на этом отрезке функция
и ветви параболы направлены вниз, то на этом отрезке функция 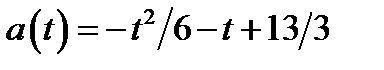 убывает. Поэтому для построения части параболы найдём следующие значения функции
убывает. Поэтому для построения части параболы найдём следующие значения функции 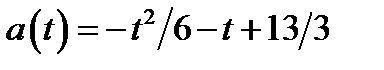 :
: 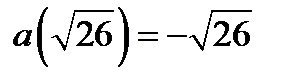 ,
, 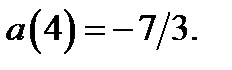
Отметим: точки 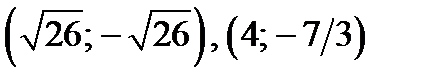 принадлежат области I.
принадлежат области I.
Строим часть параболы  где
где 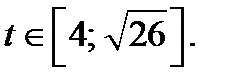
2) В области II совокупность (23.4) равносильна совокупности

а) Если 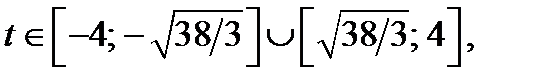 то
то 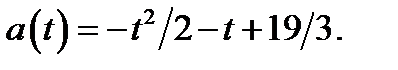
Графиком функции 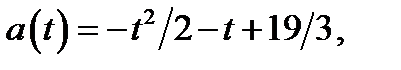 где
где 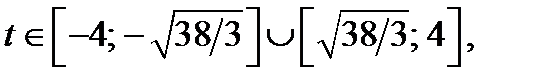 является часть параболы. Абсцисса вершины параболы
является часть параболы. Абсцисса вершины параболы 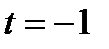 не принадлежит множеству
не принадлежит множеству 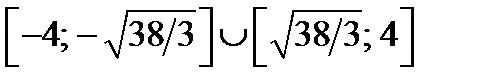 и ветви параболы направлены вниз. Поэтому для построения части параболы найдём следующие значения функции
и ветви параболы направлены вниз. Поэтому для построения части параболы найдём следующие значения функции 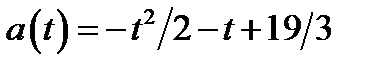 :
:

Отметим: точки 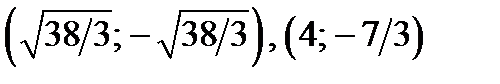 принадлежат области II, а точки
принадлежат области II, а точки 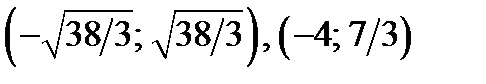 не принадлежат области II, они лежат выше оси абсцисс.
не принадлежат области II, они лежат выше оси абсцисс.
Строим часть параболы 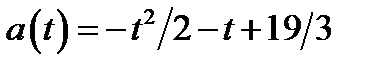 , где
, где 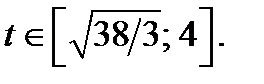
б) Если 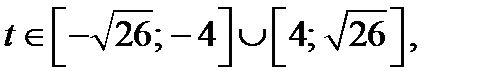 то
то 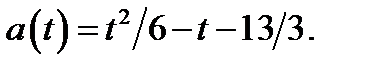
Графиком функции 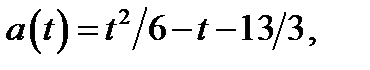 где
где 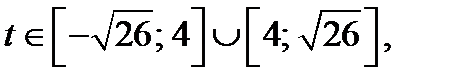 является часть параболы. Абсцисса вершины параболы
является часть параболы. Абсцисса вершины параболы 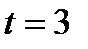 не принадлежит множеству
не принадлежит множеству 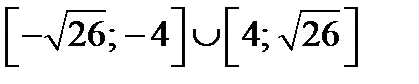 и ветви параболы направлены вверх. Поэтому для построения части параболы найдём следующие
и ветви параболы направлены вверх. Поэтому для построения части параболы найдём следующие
значения функции 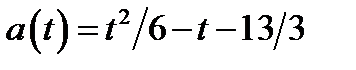 :
:
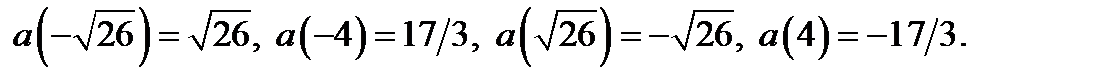
Отметим: точки 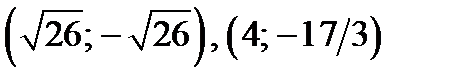 принадлежат области II, а
принадлежат области II, а
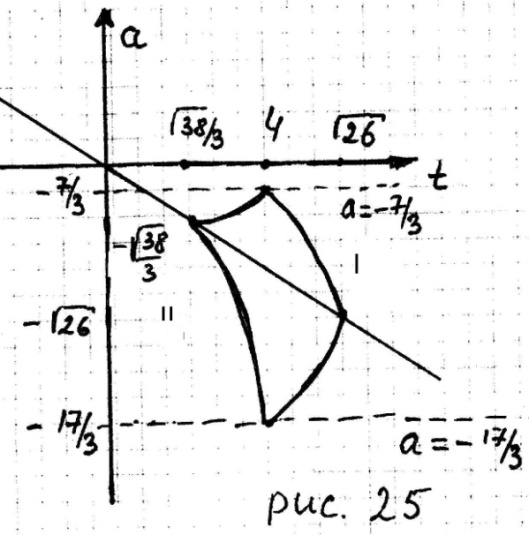 точки
точки 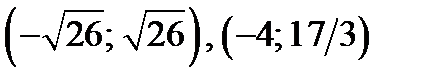 не принадлежат области II, они лежат выше оси абсцисс.
не принадлежат области II, они лежат выше оси абсцисс.
Строим часть параболы 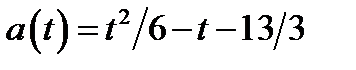 , где
, где 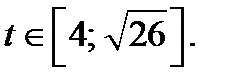
2. Из рисунка 25 следует: если 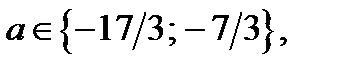 то совокупность (23.4), а значит и исходное уравнение, имеет единственный корень.
то совокупность (23.4), а значит и исходное уравнение, имеет единственный корень.
Из замечания следует, что и при 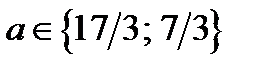 исходное уравнение имеет единственный корень.
исходное уравнение имеет единственный корень.
Ответ. 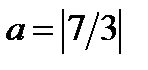 или
или 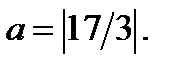
24. Сколько корней в зависимости от параметра а имеет уравнение 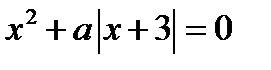 ?
?
Решение. Очевидно, что 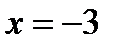 не является корнем исходного уравнения. Имеем
не является корнем исходного уравнения. Имеем
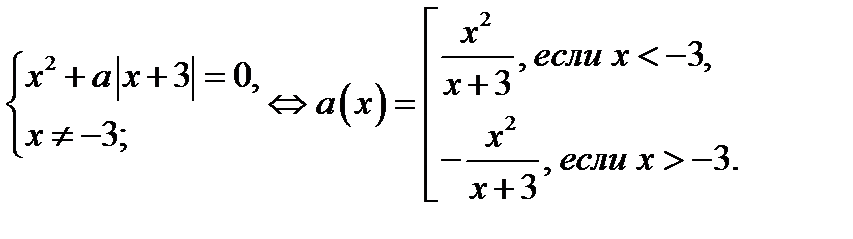
На плоскости 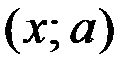 построим график функции
построим график функции 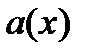 .
.
1. Очевидно, 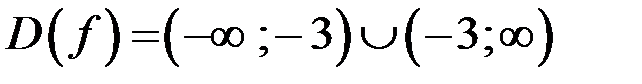 .
.
2. Найдём промежутки монотонности, точки экстремума, значения функции в точках экстремума.
а) Найдём производную функции 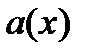 . Имеем
. Имеем
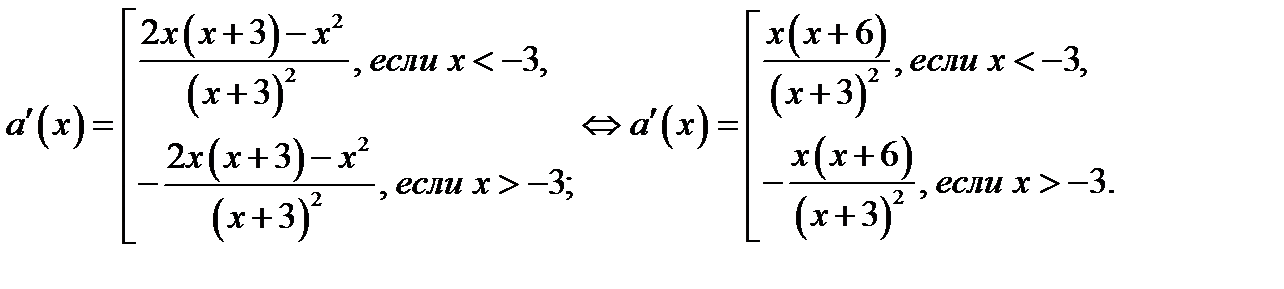
б) Из уравнения 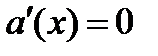 находим критические точки:
находим критические точки: 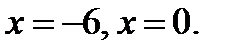
Эти точки и точка 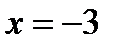 разбивают числовую прямую на интервалы
разбивают числовую прямую на интервалы 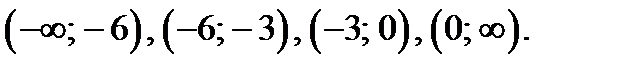
в) Определим знаки функции 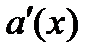 на каждом интервале (рис. 26). Надо учесть то, что функция
на каждом интервале (рис. 26). Надо учесть то, что функция 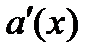 задана различными выражениями.
задана различными выражениями.
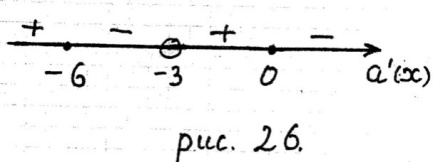 г) Из рисунка 26 делаем вывод.
г) Из рисунка 26 делаем вывод.
Функция 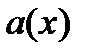 возрастает на каждом промежутке
возрастает на каждом промежутке 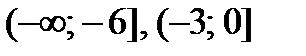
Функция 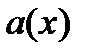 убывает на каждом промежутке
убывает на каждом промежутке 
В точках 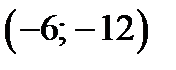 и
и 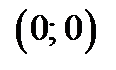 функция
функция 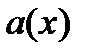 имеет максимум.
имеет максимум.
3. Рассмотрим поведение функции 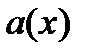 вблизи границ области определения функции. Имеем
вблизи границ области определения функции. Имеем
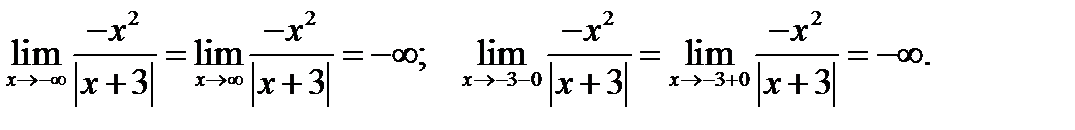
4. Строим график функции 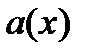 .
.
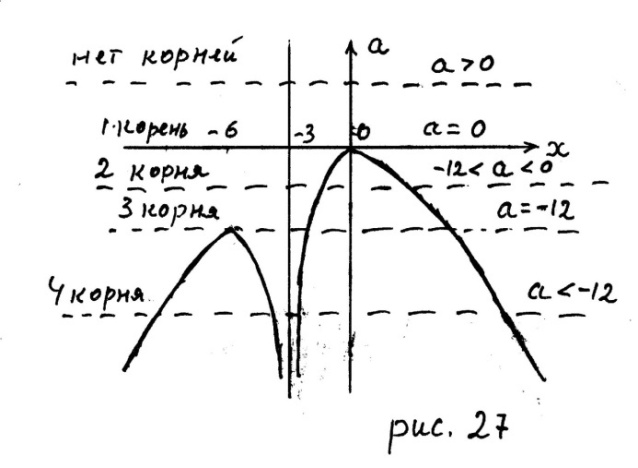
5. Из рисунка 27 (масштаб на осях координат разный) следует ответ.
Ответ. Если 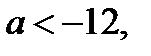 то 4 корня; если
то 4 корня; если 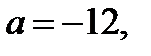 то 3 корня; если
то 3 корня; если 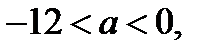 то 2 корня; если
то 2 корня; если  то 1 корень; если
то 1 корень; если 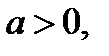 то корней нет.
то корней нет.
25. Сколько корней в зависимости от параметра а имеет уравнение 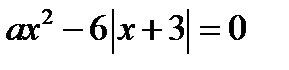 ?
?
Решение. Очевидно, что 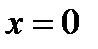 не является корнем исходного уравнения.Имеем
не является корнем исходного уравнения.Имеем
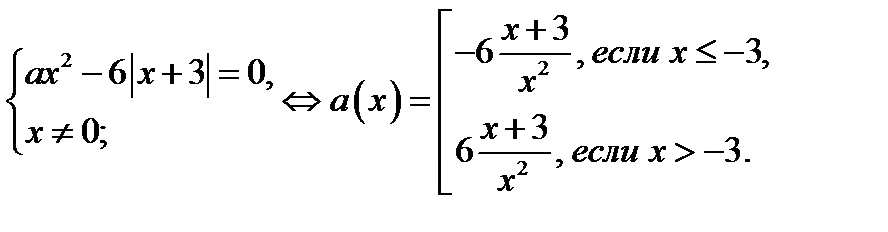
На плоскости 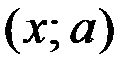 построим график функции
построим график функции 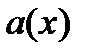 .
.
1. Очевидно, 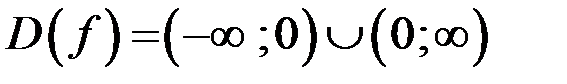 .
.
2. Найдём промежутки монотонности, точки экстремума, значения функции в точках экстремума.
а) Найдём производную функции 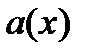 . Имеем
. Имеем
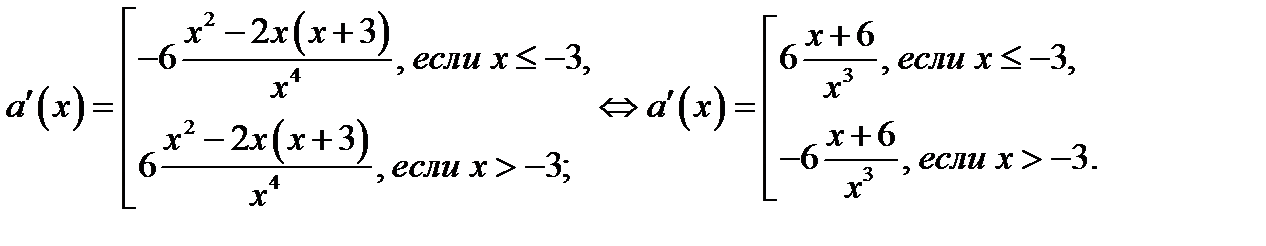
б) Из уравнения 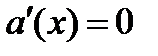 находим критическую точку:
находим критическую точку: 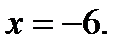
Кроме того,критической точкой является точка 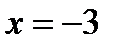 (функция
(функция 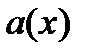 в этой точке определена, а производная не существует).
в этой точке определена, а производная не существует).
Эти точки и точка 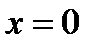 разбивают числовую прямую на интервалы
разбивают числовую прямую на интервалы 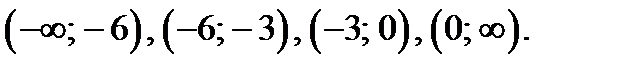
в) Определим знаки функции 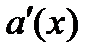 на каждом интервале (рис. 28). Надо учесть то, что функция
на каждом интервале (рис. 28). Надо учесть то, что функция 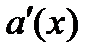 задана различными выражениями.
задана различными выражениями.
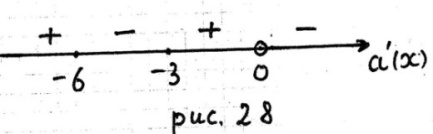 г) Из рисунка 28 делаем вывод.
г) Из рисунка 28 делаем вывод.
Функция 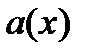 возрастает на каждом промежутке
возрастает на каждом промежутке 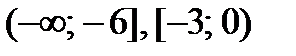
Функция 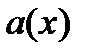 убывает на каждом промежутке
убывает на каждом промежутке 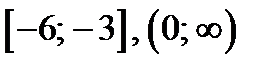 . Функция
. Функция 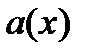 в точке
в точке 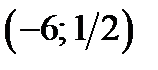 имеет максимум, а в точке
имеет максимум, а в точке 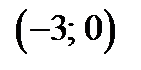 – минимум.
– минимум.
3. Рассмотрим поведение функции 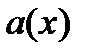 вблизи границ области определения функции. Имеем
вблизи границ области определения функции. Имеем
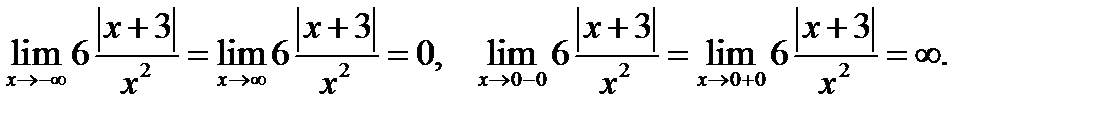
 4. Строим график функции
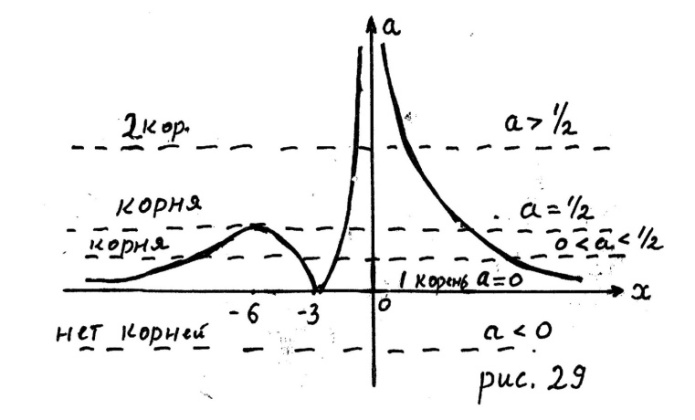
4. Строим график функции 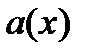 (рис. 29).
(рис. 29).
5. Из рисунка 29 (масштаб на осях координат разный) следует ответ.
Ответ. Если 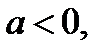 то корней нет; если
то корней нет; если  то 1 корень; если
то 1 корень; если 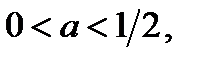 то 4 корня; если
то 4 корня; если 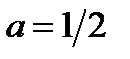 , то 3 корня; если
, то 3 корня; если 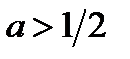 то 2 корня.
то 2 корня.
26. Решите уравнение 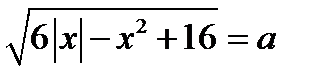 .
.
Решение. 1. Так как 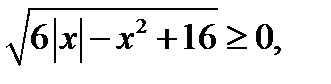 то при
то при 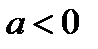 уравнение решений не имеет.
уравнение решений не имеет.
Замечание. Точки 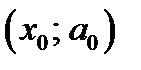 и
и 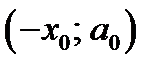 одновременно удовлетворяют уравнению
одновременно удовлетворяют уравнению 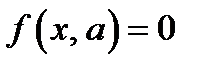 . Поэтому можно сначала решить уравнение
. Поэтому можно сначала решить уравнение 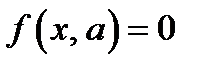 при
при 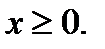
2. Так как точки (х; а) и (–х; а) одновременно удовлетворяют исходному уравнению, то рассмотрим это уравнение при 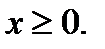
Имеем
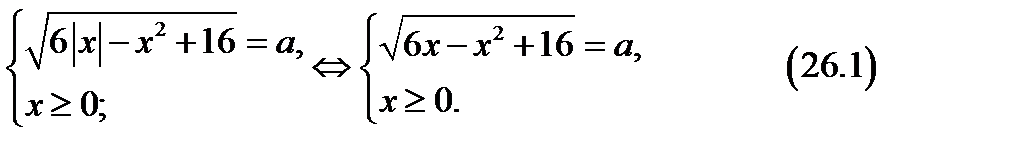
Из системы (26.1) следует, если 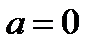 , то
, то 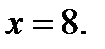
3. Рассмотрим систему (26.1) при 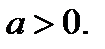 Имеем
Имеем
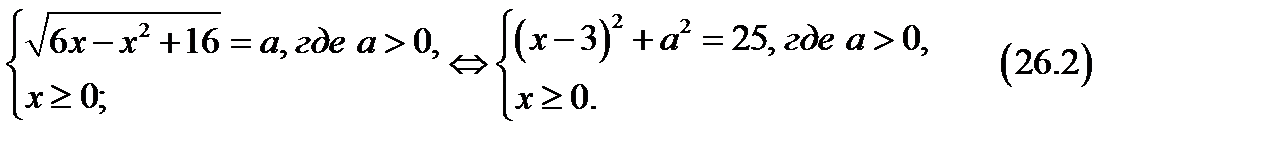
3. Графиком системы (26.2)является часть окружности с центром в точке (3; 0) и радиусом, равным 5.
Построим график системы (26.2) на плоскости х0а.
а) Точку пересечения графика системы (26.2) с осью 0а найдём из системы 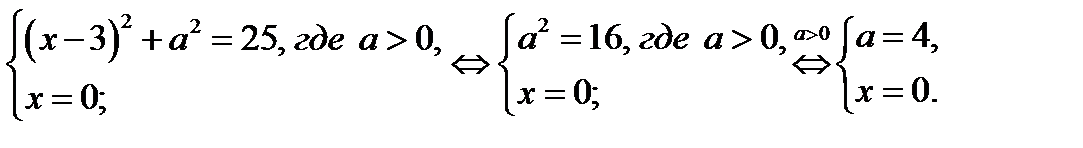
Итак, график системы (26.2) проходит через точку (0; 4).
Строим часть окружности 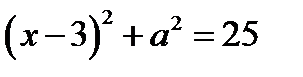 при
при 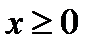 и
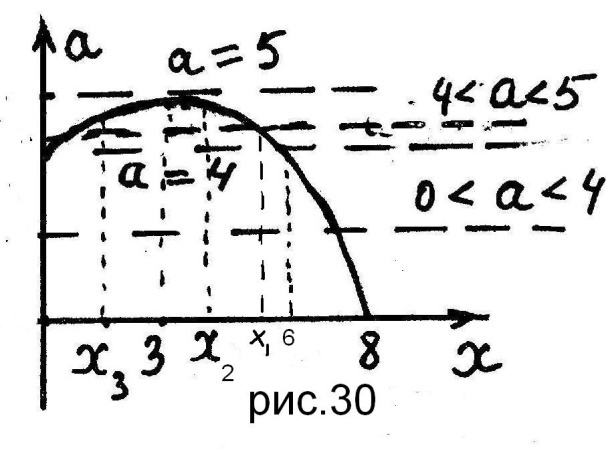
и 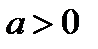 . 5. Из рисунок 30 следует, что система (26.2) имеет
. 5. Из рисунок 30 следует, что система (26.2) имеет
один корень 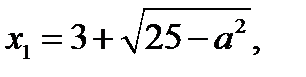 если
если 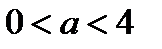 ; один корень
; один корень 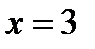 , если
, если 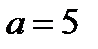 ;
;
два корня: 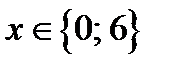 , если
, если 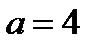 ; два корня:
; два корня: 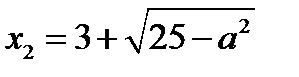
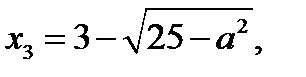 если
если 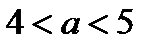 ;
;
корней не имеет, если 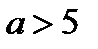 .
.
Из замечания, а также из 1. для исходного уравнения следует ответ.
 Ответ. Если
Ответ. Если 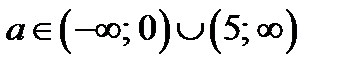 , то корней не имеет;
, то корней не имеет;
если 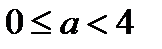 , то два корня:
, то два корня: 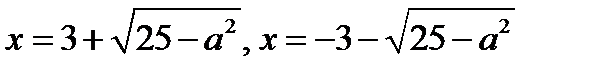 ;
;
если 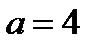 , то три корня:
, то три корня:  ;
;
если 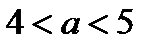 , то четыре корня:
, то четыре корня: 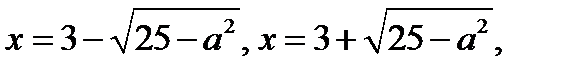
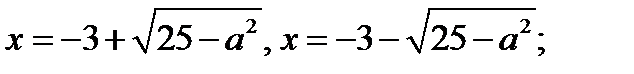
если 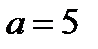 , то два корня:
, то два корня: 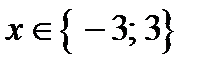 .
.
27. Найдите все значения параметра а, при которых уравнение 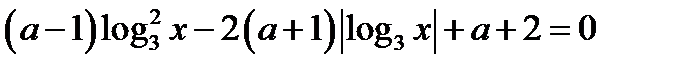 имеет четыре корня.
имеет четыре корня.
Решение. 1. Исходное уравнение при 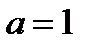 имеет два корня, так как оно принимает вид
имеет два корня, так как оно принимает вид 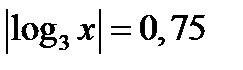 .
.
2. Пусть 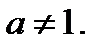
Сделаем замену 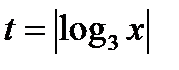 , где
, где 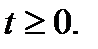
а) Если 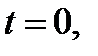 то уравнение
то уравнение 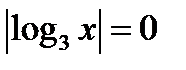 имеет единственный корень. Для любого
имеет единственный корень. Для любого 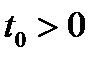 уравнение
уравнение 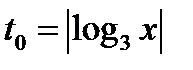 имеет два различных корня
имеет два различных корня
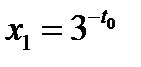 или
или 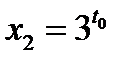 .
.
б) Пусть 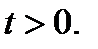
Так как  и
и 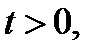 то исходное уравнение принимает вид
то исходное уравнение принимает вид
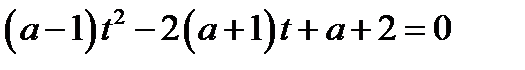 , где
, где 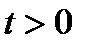 и
и 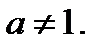 (27.1)
(27.1)
Исходное уравнение имеет четыре корня, если уравнение (27.1) имеет два различных положительных корня.
Так как 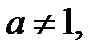 то уравнение (27.1) равносильно уравнению
то уравнение (27.1) равносильно уравнению
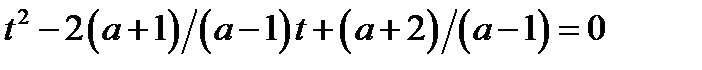 (27.2)
(27.2)
Замечание. Квадратное уравнение 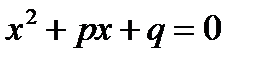 имеет два положительных корня тогда и только, когда
имеет два положительных корня тогда и только, когда 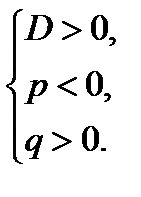
Итак, квадратное уравнение (27.2), а значит и квадратное уравнение (27.1) имеет два положительных корня тогда и только, когда выполняется условие
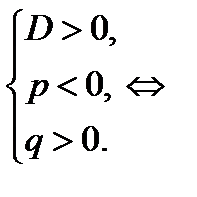

Итак, квадратное уравнение (27.2) имеетдва положительных корня,если 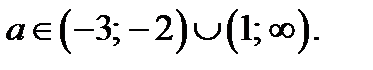 Тогда исходное уравнение имеет четыре различных корня при
Тогда исходное уравнение имеет четыре различных корня при