Изучение затухающих колебаний
1 Дифференциальное уравнение RLC-контура
2 Затухающие колебания
3 Параметры затухающих колебаний
Основные понятия по теме
На рисунке 10.1 показана электрическая цепь, используемая для изучения свободных электромагнитных колебаний. Ключ К сначала приводят в положение 1, при этом происходит зарядка конденсатора от источника постоянного напряжения ε0. Затем ключ К переводят в положение 2, при этом источник ε0 отключается от цепи, однако цепь остается замкнутой, и в ней возникают свободные электромагнитные колебания. При таких колебаниях происходит обмен энергией между конденсатором и катушкой, и этот процесс периодически повторяется, сопровождаемый тепловыми потерями. Другими словами, энергия электрического поля преобразуется в энергию магнитного поля и обратно, при этом часть энергии рассеивается в виде тепла.
| ε0 |
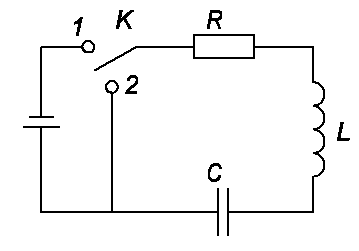
Рисунок 10.1 – RLC-контур
Для такой цепи, содержащей R-, L- и C-элементы (рисунок 10.1), в которой происходят свободные (в отсутствие внешнего напряжения) электромагнитные колебания, согласно второму закону Кирхгофа, можно записать:
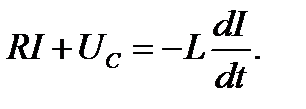
Здесь UC– напряжение на конденсаторе,
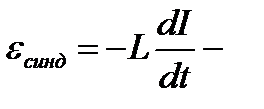 э.д.с. самоиндукции, возникающая в катушке.
э.д.с. самоиндукции, возникающая в катушке.
Выражая UCчерез заряд q, получим
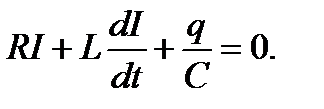
Дифференцируя по времени и учитывая, что сила тока равна
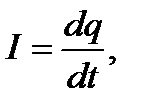
получаем:
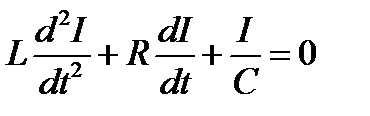 .
.
Вводя собственную частоту колебательной системы 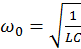 и коэффициент затухания γ = R/2L, перепишем уравнение в виде
и коэффициент затухания γ = R/2L, перепишем уравнение в виде
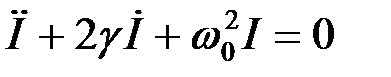 .
.
Здесь точки обозначают дифференцирование по времени.
Решая это уравнение, можно показать, что, в зависимости от соотношения между параметрами ω0 и γ, возможны следующие типы колебаний в контуре:
| I |
| I1 |
| I2 |
| t1 |
| t2 |
| t |
| I0 |
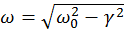 – частота, δ – начальная фаза колебаний, I0 – их начальная амплитуда (рисунок 10.2).
– частота, δ – начальная фаза колебаний, I0 – их начальная амплитуда (рисунок 10.2). Рисунок 10.2 – График затухающих колебаний в контуре 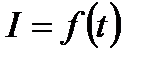
Величины δ и I0 могут быть определены из начальных условий. Для характеристики затухающих колебаний вводятся также такие величины, как период колебаний («повторения нулей»)
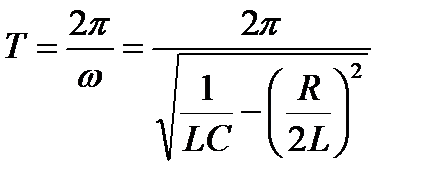 ,
,
логарифмический декремент затухания, который показывает уменьшение амплитуды за период колебаний
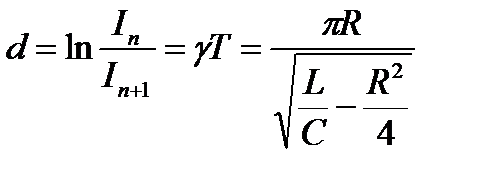 ,
,
и добротность контура, физический смысл которой заключается в отношении запасенной в контуре энергии к энергии потерь за период колебаний
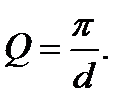
Здесь In и In+1 – значения силы тока в моменты времени, отстоящие друг от друга на один период колебаний;
б) апериодическое затухание силы тока в контуре, которое наблюдается в случае ω02 – γ2 < 0. При этом сила тока монотонно убывает до нуля по закону 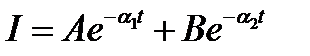 , где
, где 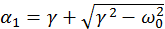 и
и  , А и В – величины, определяемые из начальных условий (рисунок 10.3).
, А и В – величины, определяемые из начальных условий (рисунок 10.3).
| t |
| I |
| А+В |
Рисунок 10.3 – Апериодические затухания силы тока в контуре
в) критический режим изменения силы тока, который имеет место при выполнении соотношения ω02 – γ2 = 0 и представляет собой предельный случай рассмотренных выше затухающих колебаний и апериодического режима. При этом зависимость силы тока от времени можно записать в виде
I = (A + Bt)e –γt,
где значения постоянных А и В определяются из начальных условий. График зависимости в случае А = 0, В ¹ 0 и А ¹ 0 , В = 0 представлен на рисунке 10.4.
Сопротивление 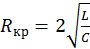 , при котором выполняется соотношение
, при котором выполняется соотношение
ω02 - γ2 = 0, называется критическим сопротивлением.
| В=0 |
| А=0 |
| t |
| I |
Рисунок 10.4 – График зависимости 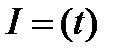
в случаях А ¹ 0, В = 0 и А = 0, В ¹ 0 при критическом режиме
Если колебательный процесс изучать в системе координат I–U, где I – сила тока в контуре, U – напряжение на конденсаторе, то плоскость I–U называют фазовой плоскостью, а кривую, изображающую такую зависимость, называют фазовой кривой (рисунок 10.5).
При затухающих колебаниях амплитуда напряжения и силы тока в контуре убывает, а фазовая кривая превращается в спираль, приближающаяся к фокусу 0. При R ≥ Rкр колебательный процесс прекращается, и спираль превращается в окружность.
| I |

| U |
| U0 |
Рисунок 10.5 – Колебательный процесс на фазовой плоскости
Вопросы для самоконтроля
1 Приведите уравнение, описывающее затухающие колебания в контуре, содержащем R, L и C.
2 Охарактеризуйте следующие параметры: коэффициент затухания, логарифмический декремент затухания, добротность контура.
3 Приведите определение критического сопротивления Rкр контура.
Лабораторная работа 10
