Дифференциалды теңдеулер, өтпелі және беріліс функциялары, жиіліктік сипаттамалары

Дифференциялдық теңдеуді шешу қандай да бір заңдылық бойынша өзгеретін кіріс шаманы кіріс шаманы кіріске беру кезінде шығыс шаманың уақыт бойынша өзгерісін бейнелейді. әртүрлі заңдылықтарда кіріс шаманың әртүрлі түрде өзгерісі уақыт бойынша өзгереді және шығыс шама (2–14) дифференциялдық теңдеуден өтпелі функцияны тауып аламыз. Егер бұл теңдеуде кіріс шама ретінде сатылы әсерді қабылдап алсақ

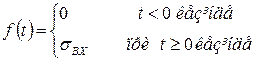(2-16)

онда (2-14) теңдеуц келесі түрде болады

.

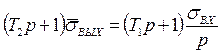Ол теңдеудің шешімі

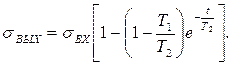
Егер кіріс шама ретінде бірлік секіріс түріндегі әсерді қабылдасақ, яғни 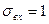болса, онда өтпелі функцияның теңдеуін аламыз

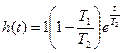(2.17)

ол кіріс шаманың нөльдін бірге дейін сатылы өзгеруі кезіндегі жүйенің (немесе үзбенің) өтпелі процесін бейнелейді. 2.6. суретте (2.17) өрнек бойынша құрылған өтпелі функцияның графигі келтірілген

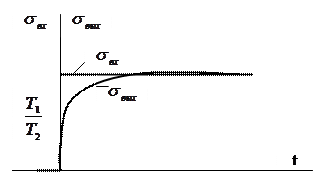
2.6. Сурет. Өтпелі функцияның графигі

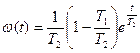(2.18)

бұл өрнек бірлік импульсті ( 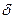–функцияны) берген кездегі жүйенің өтпелі процесін бейнелейді.

(2.8) және (2.14) теңдеулері шығыс шаманың бейнесінің кірістен тәуелділігін бейнелейді. (2.4) теңдеуңн түрлендіріп келесі түрде жазамыз:

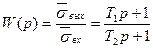(2.19)

(2.19) өрнегі беріліс функциясы деп аталады. Сондан динамикалық жүйенің W(p) беріліс функциясы шығыс шамасының Лаплас бойынша бейнеленуінің кіріс шамасының Лаплас бойынша бейнеленуіне нөльдік бастапқы шарттардағы қатынасын айтамыз. өрнегінен мынаны аламыз.

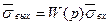(2.20)

біздің мысалымызда қарастырылып жатқан схеманы 2.7.суретте келтірілген W(p)–мен беруге болады. Мұндағы кіріс және шығыс шамалар – сәйкес белгілеулерімен тік жолмен берілген, ал схема беріліс функциясы жазылған тікбұрышпен бейнеленген. Нөльдік бастапқы шарттардағы схема Лаплас бойынша бейнелеу аймағында шығыс шаманы алу үшін кіріс шаманы беріліс функцияға көбейту операторы ретінде қарастырылуы мүмкін.

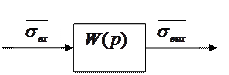
2.7. Сурет. Мысалға блок–схема

Лаплас бойынша (2.17) беріліс функциясы өрнегін түрлендіріп, аламыз.

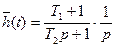(2.21)

немесе (2.20) өрнегін ескере отырып

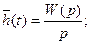
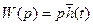(2.22)

Осылай, беріліс функциясы өзінше Лаплас бойынша түрлендірілген беріліс функцияны береді (уақыт бойынша алынған туынды ауданына алымға теңәсердің бейнелену ауданына p көбейту) өтпелі функциясы мен беріліс функциясы жүйенің уақыт бойынша ауданына және Лаплас бойынша бейнелену сәйкес динамикалық қасиеттерін бейнелейді.

Жоғарыда келтірілген барлық пікірлер кез–келген сызықтың автоматты реттеу жүйесі немесе оның жеке элементтері үшін әділітті.

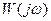Кіріс сигналының кез–келген тіркелген жиілігінің мәніндегі өзінше 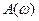ампилтудасы және 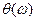аргументті векторды береді. –нің 0–ден ∞–ке дейін өзгеруінен көптеген әртүрлі векторлар аламыз. Осы векторлардың ұштары арқылы өткен басып амплитудалы–фазалы сипаттамасы (а.ф.х) деп аталады, ал (2–25) өркен беріліс функцияның жиілігі деп аталады.

Осылай, амплитудалы – фазалы сипаттама деп радиус – векторлардың ұштарын қосатын сызықты айтамыз, оның ұзындығы кіріс пен шығыс сигналдардың амплитудасының қатынасына тең, ал нақты өсьтің оң бағытынан туған бұрыш 0–ден ∞–ке дейін өзгеретін жиілік үшін кіріс пен шығыс сигналдар фазаларының айырымына тең. (2-19) бен (2-25) өрнектерін салыстыра отырып, амплитудалы-фазалы сипаттаманың теңдеуін 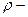ді 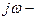ға алмастырған беріліс функцицядан алыну мүмкін. Бұл жалпы ереже болып табылады және олар әрқашан пайдаланады.

Динамикалық жүйенің өтпелі функциясы мен амплитуда-фазалы сипаттамасы арасында тығыз байланысы бар, өйткені олар бірдей деференциялды теңдеулерден салынады. Бірінші жағдайда жүйенің кірісіне бірлік секіріс түріндагі әсер беріледі, ал екінші жағдайда-синусоидалық әсер. Бұл байланыс жүйесінің амплитудалы-фазалы сипаттамасы бойынша теңдейді шешпей-ақ оның өтпелі процесін құруға мүмкіндік береді. Ол үшін әдетте амплитуда-фазалы сипаттаманың заттай бөлігі қолданылады.

Өтпелі функцияның графигі бойынша өтпелі функцияның барлық ординаттарын кіріс шамаға көбейте отырып сотылы әсер кездегі өтпелі процес графигін алуға болады.

Ереже бойынша, жүйенің амплитуда – фазалы сипаттамасының W (j ) теңдеуі дәрежедегі пошнама болып табылатын түбірді алымымен бөлігін береді. Егер алымындағы пошнои дәрежесі бөліміндегі пошнои дәрежесінен жоңары болса, онда 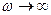болғанда

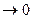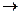
W (j ) болады. Егер алымындағы пошнои дәрежесі бөлімінің пошнои дәрежесіне тең болса, онда 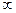болғанда.

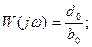
мүндағы ₀ мен b₀ - сәйкесінше алымы мен бөліміндегі жоғары дәрежелердегі коэффициенттер.

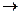
Құрастырылған жағдайда 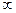болғанда

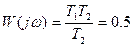
Амплитудалы – фазалы сипаттама айғақты өсіне қатысты симметриялы . Егер + мәнінің орнына - –ді қойсақ, онда айғақты өсьтегі бірінші қисықтың айналу бейнесін аламыз.

Кейбір жағдайларда кері амплитуда – фазалы сипаттама қолданылады.

;

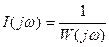Қарастырылып жатқан мысал үшін

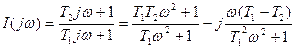
2.8. сурет б–да Т₁=1 сек, T₂=2 сек мәні үшін кері амплитуда – фазалы сипаттама келтірілген. Бұл да жартылай шеңбер, біраө оның радиусы қарапайым а.ф.с.–ға қарағанда үлкен және оң жалған (жорамал) бөлікті.

(2.26) өрнектен айғақты бөлігін жазып аламыз

;

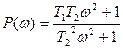және жорамал бөлігі

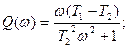
Бұл екі өрнектер жиілігіне тәуелді және айғақты және жорамал жиіліктің сипаттамаларының теңдеуіне сәйкес болып табылады.

(2.29) өрнегін логарифмдейміз

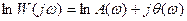; (2.34)

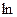A( )және 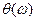өрнектері бойынша жиіліктік логарифмдік маштабында құрылған қисықтар сәйкесінше логарифмді амплитудалы және логарифмді фазалық жиіліктік сипаттамалар деп аталады (сурет. 2–10). Кейде жиілікті қандай да бір тұрақты мәнге бөледі, сонда абцисса өсі бойынша жиіліктің қатысы өлшемсіз мәндері логарифмдік масштабта кейінге қалдырылады. Логарифмдік шкаланың негізгі бірліктері октава және декада болып табылады.

Октава деп жиілігі мен оның екі еселенген 2 мәні арасында бекітілген жиіліктер аралығын айтамыз. Октаваны бейнелеуші кесінді шкаланың кез – келген аймағында бірдей ұзындыққа ие және 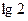–ге тең.

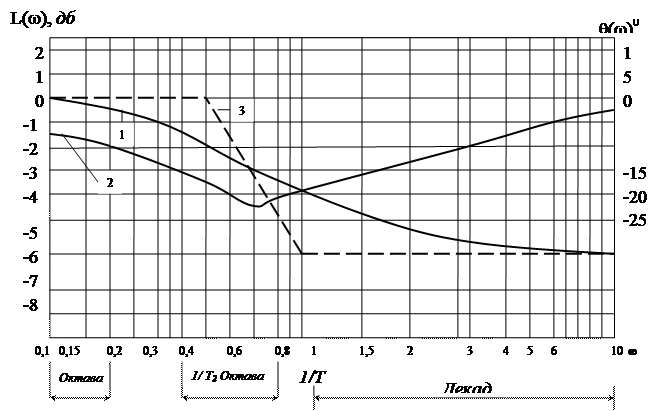
2.10. Сурет. Логарифмдік жиіліктік сипаттамалар

Декада деп жиілігінің еркін мәні мен оның жаңарлаған және он есе үлкейген 10 –ға тең.

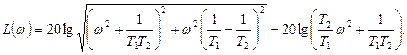(2-35)

Логарифмдік амплитудалы жиіліктік сипаттаманы құру кезінде өсь бойынша 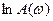емес, ал оған пропорционалды 20 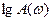шамасы кейінге қалдырылады, ол шама децибельде өлшенеді. Егер L децибельде берілген қандай да В санының мәні болса, онда 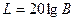болады.

Логарифмдік фазалы жиіліктік сипаттаманы құру кезінде ордината өсі бойынша кіріс пен шығыс сигналдары арасындағы фазалардың жылжу бұрышы градуспен қалдырылады. Қарапайым мысал үшін логарифмдік жиіліктік сипаттаманы құрамыз. Амплитуда логарифмдік жиілікті сипаттамасының теңдеуін (2.32) өрнегін логарифдей отырып аламыз.

Т₁=1 сек және Т₂=2 сек болғанда жиіліктің әртүрлі мәндерін (2.35) қоя отырып, L( ) амплитудасының децибильдегі сәйкес мәндерін анықтаймыз (2.1 кесте) және есептеулер нәтижелері бойынша нүктелер бойынша амплитудалы жиіліктік сипаттаманы құрамыз (2.10 суреттегі 1–қисық). Көп санды қисықтардың оларды логарифмдік масштабта тұрғызу кезіндегі қисықтығы азаяды. Бұл жағдайда көбінесе амплитудалы логарифмдік сипаттамаларды сынған түзетулермен аппроксимациялау үшін қолданылады, ол жіктелуді едәуір қысқарту мүмкін болмай шығады, өйткені үлкен қателіктер тудырады.

Логарифмді фазалы жиіліктік сипаттаманың нүктелерінің координаттарын (21.10, суретте 2–қисық). Т₁=1сек, және T₂=2сек болғанда (2.33) өрнектің көмегімен есептейміз. Есептеу нәтижелері 2.2– кестеге орналастырылған.

Логарифмдік қисықтардың нүктелері бойынша есептеу аса күрделі жұмыс, бірақ сипаттаманы комплекстік жазықтықта құруға қарағанда жеңіл. Егер жорамал сыну қисығын құрсақ, есептеу жұмысы лезде қысқартылады.

дәрежедегі 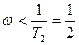кіші жиіліктегі (2–35) өрнегін с 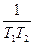– мен салыстырғанда қарастыруға көңіл бөлмеуге болады. Бұл кезде (2–35) өрнегі мына түрге келеді.

,

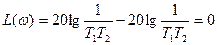яғни сипаттама абсцисса өсімен сәйкес келеді.

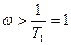жиілігінің үлкен мәндері кезінде, жоғары дәрежедегі –дан бөлек барлық бөлшектерді елемеуге болады. Осыдан

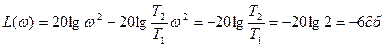
Осылай, 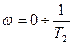мәндердегі лоарифмді амплитудалы жиіліктік сипаттама абсцисса өсімен сәйкес келетін түзукесіндісімен, 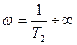мәндерінде абсцисса өсіне параллель және 6 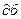–ға қалып қоятын түзумен бейнеленеді. Дәл нүктеге жақын (дәл нүктеден кем дегенде 3 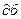–ға ерекшеленеді) жақындатылған сипаттаманы аламыз (2–10 суреттегі 3 сынық). 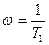және 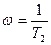жиіліктері жанасушы сипаттаманы көп жағдайларда толығымен құру қажет емес, тек қандай да бір нүктедегі кіріс және шығыс сигналдары арасындағы фазалардың ығысуын анықтау қажеттілігі туады, ол күрделі қиыншылық тудырмайды. Сонымен қатар белгілі амплитудалы логарифмдік сипаттама кезіндегі нүктедегі фазалардың ығысуын анықтаудың жорамал әдістері өңделген. Дегенмен олардың тек массалы бір типті есептеулер кезінде ғана мәндері болады. Эпизодтың есептеулер кезінде жорамал әдістер мен оларды пайдалану ауданын оқып білу бірнеше нүктелерді дәл есептеуге қарағанда үлкен уақытты алады.

2-1 кесте

	0,1	0,2	0,4	0,6	0,8	1,0	2,0	4,0	8,0	10,0	20,0
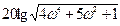	0,21	0,83	2,79	5,21	7,63	10,00	19,29	30,43	42,23	46,08	58,08
-20lg(4 2+1)	-0,34	-1,29	-4,30	-7,75	-11,03	-13,98	-24,61	-36,26	-48,20	-52,06	-64,08
L( ), 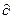б	-0,13	-0,46	-1,51	-2,54	-3,39	-3,98	-5,31	-5,83	-5,97	-5,98	-6,00

Кесте

		0,1	0,2	0,4	0,6	0,8	1,0	2,0	4,0	8,0	10,0	20,0	∞
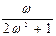		0,1	0,185	0,300	0,347	0,351	0,33	0,222	0,121	0,062	0,050
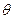		50 40/	100 40/	170 30/	200 20/	200 30/	190 20/	120 50/	70 00/	30 30/	20 50/

Негізгі әдебиет: 1[5-28; 42-54]; 2 [15-33; 73-92].

Қосымша әдебиет: 1 [8-70]; 2 [3-30].

Бақылау сұрақтары:

1. Басқару, автоматты басұару дегеніміз не?
2. АБЖ дегеніміз не?
3. АБЖ қандай функциялапр қойылады?
4. Типтік әсерлерді не үшін қолданады және олардың түрлері?
5. Кіріс және шығыс шамалары дегеніміз не?
6. Кері байланыс түрлері.
7. Статикалық және астатикалық реттеу деп нені айтамыз?
8. АБЖ қандай талаптар қйылады:
9. АРЖ талдау оны синтездеуден қалай ерекшеленеді:
10. Типтік динамикалық буындардың қандай түрлері бар:

№ 2 дәрістің конспектісі

Дәрістің тақырыбы: 1.2. АРЖ–ң типтік буындары, олардың беріліс функциялары мен жиіліктік сипаттамалары. (Жүйе элементтерін типтік динамикалық буындарға жіктеу әдісі. Типтік буындардың – инерциясыз, Ι ретті инерциялы, ΙΙ ретті инерциялы және тербелістік, интегралдаушы, дифференциялдаушы мен кешігу буындарының жиілік сипаттамасының беріліс функциясы мен аналитикалық өрнектерін анықтау).

Автоматты реттеу жүйелері олардың элементтерінің жеке құраушыларының әртүрлі тәсілдермен мүшеленуі мүмкін.

Тәсілдердің бірі жүйе жеке элементтерге олардың қойылымы бойынша, функционалды белгілері бойынша мүшеленеді, мысалы. Реттеу объектісі, басқарушы элемент, орындаушы механизм және т.б. бөлектенеді.

Жүйені конструктивті рәміздеуі бойынша элементтерге мүшелеуге болады (мысал, генератор, электромашиналы күшейткіш, потенциометр).

Дегенмен автоматты реттеу жүйесінің төзімділігі мен сапасын зерттеу кезінде элементтерді олардың динамикалық қасиеттері бойынша бөлу маңызды. Жүйе элементтерін осы көз қараста қарастыру, әртүрлі әрекет принциптері мен әртүрлі конструктивті бейнеленетін әртүрлі элементтер бірдейдифференциялды теңдеулермен жазылады және динамикалық қасиеттері де бірдей, өздерін өтпелі процестерде бәрдей алып жүретінін көрсетеді.

Өзіңіз динамикалық қасиеті жағынан қарастырылатын элемент буын деп аталады. Шоғырланған параметрлері кез­-келген сызықтық жүйе осындай қарапайым жай элементтерге бөлінуі мүмкін. Буынның өтпелі процестері қарапайым дифференциялды теңдеулермен бейнеленеді, олардың әрқайсысының реті екіден жоғары емес. Автоматты реттеу жүйесінің барлық нақты элементтері бөліне алатын үзбелер типінің саны онша үлкен емес. Келесі буындарды ажыратады: күшейткіш, апериодты, тербелістік, интегралдаушы, дифференциялдаушы, кешігу.

Жүйенің типтік буындарға мүшеленуі оның функционалды немесе конструктивті элементтерге мүшеленуімен сәйкес болмауы мүмкін.

Теориялық түрде буынның санын аса үлкен қылып беруге болады, дегенмен оларды физикалық түрде іске асыра алмайды, не анық қанағаттанарсыздық динамикалық қасиеттердің салдарынан тәжірибе жүйесінде қолданылмайды. Кейбір жағдайларда есептеуді жеңілдету үшін физикалық түрде іске асырылуға берілмейтін көрінетін буындар қарастырылады. Бұл тәжірибеде толық жарамайтын есептеулердің нәтижелеріне кейбір қателіктер енгізеді. Жоғарыда айтылған буындарды қарастырған кезде жолай басқа да көрінетін және қолданылмайтын буындар көрсетіледі.