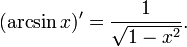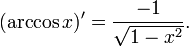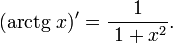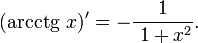Свойства. Парабола — кривая второго порядка

Парабола — кривая второго порядка.

· Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.

· Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.

· Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

· Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

28. Уравнения 2 порядка решаются по правилам замены и вычитания , правилам крамера. Геометрическая интерпретация???

29. 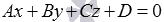т.к удовлетворяет любая точка проходящая на плоскости

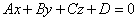
приводится к нормальному виду (1) умножением на нормирущий множитель, определяемый формулой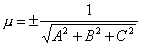

;

30. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

Если задано уравнение плоскости A

x + By + Cz + D = 0, то расстояние от точки M

(M_x, M_y, M_z) до плоскости можно найти, используя следующую формулу

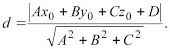
31. 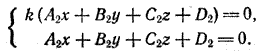Пересечение

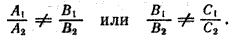
Из евклидовой геометрии известен признак параллельности двух плоскостей: две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой.

32. известно, что две различные точки определяют в пространстве прямую. Выберем в пространстве две точк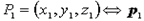и и 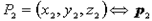и проведем 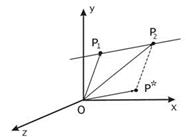через них прямую.

Проведем от точки 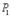к точке 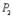вектор 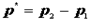. Тогда радиус-вектор 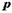, определяющий некоторую точку на прямой, можно получить сложением, например, вектора 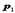и вектора 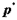, умноженного на некоторое число 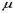. Или 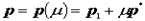. Следующая система уравнений является параметрическими уравнениями прямой:

,

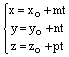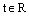
где 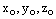– координаты произвольной фиксированной точки данной прямой, 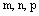– соответствующие координаты произвольного направляющего вектора данной прямой, t – параметр.

Уравнение прямой, проходящей через две данные точки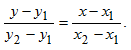

33. Ур.плоскости по 3 точ. Берешь векторное произведение AB x AC, скажем, получится ni+mj+lk
Плоскость : n(x-Ax)+m(y-Ay) + l(z-Az) = 0 + рисунок

34. Если прямая не лежит в плоскости и не параллельна ей, она пересекает плоскость.

Если прямая a, не лежащая в плоскости 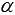, параллельна некоторой прямой b, которая лежит в плоскости , то прямая a параллельна плоскости .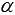

Если одна из двух параллельных прямых параллельна некоторой плоскости, то вторая прямая либо также параллельна этой плоскости, либо лежит в ней.

Прямая лежит в плоскости è

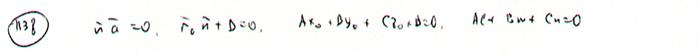
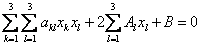35. Поверхность 2-го порядка в трехмерном пространстве

где 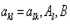- заданные постоянные числа, а 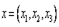- переменная точка в , определяет, вообще говоря, некоторое множество точек в , называемое поверхностью второго порядка. Если уравнение (1) не удовлетворяется ни одной действительной точкой 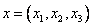, то говорят, что оно определяет мнимую поверхность

36. классификация поверхности второго порядка в трехмерном пространстве???

37. Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел.Действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль.числовая прямая — это прямая, на которой выбраны:некоторая точка O — начало отсчёта;положительное направление, указанное стрелкой;масштаб для измерения длин. действительная функция одной действительной переменной?????

38. Преде́л фу́нкции в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Предел суммы/разности двух функций равен сумме/разности их пределов:

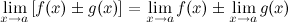
Предел произведения двух функций равен произведению их пределов:

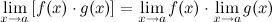
Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

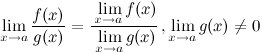
Константу можно выносить за знак предела:

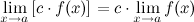
Предел степени с натуральным показателем равен степени предела:

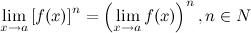
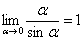– тот же самый первый замечательный предел.

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают т.е 1 число. Ограниченная последовательность бывает сверху , снизу , сверху и снизу , неограниченная. Пределом последовательности называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Второй замечательный предел Важно лишь, чтобы она стремилась к бесконечности.

40.Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.Непрерывная функция — функция без «скачков»

41. Функцию комплексной переменной можно записать в виде:
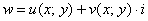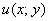, где и 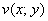– две функции двух действительных переменных.Функция 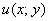называется действительной частью функции .Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. Механический смысл производной: производная от координаты по времени есть скорость v(t)=x'(t).

42. произведения:Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо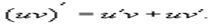

Частного: Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

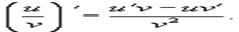
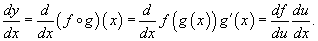Сумма: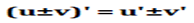

43.

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции.

Тогда обратная функция в точке y0=f(x0) имеет производную, которая может быть найдена по форумуле (f−1(y0))′=1f′(x0).

44. 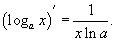èлогарифмическая 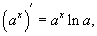è показательная

45.

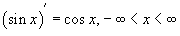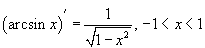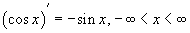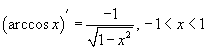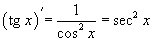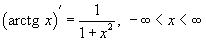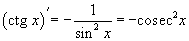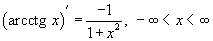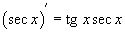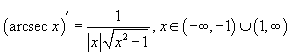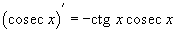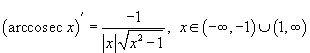46. Обратные тригнометрические

.