Множественный коэффициент корреляции

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

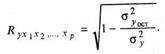
значение индекса множественной корреляции лежит в пределах от 0 до 1 и чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

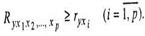
При правильном включении факторов величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости.

Если же дополнительно включенные в уравнение множественной регрессии факторы второстепенны, то индекс множественной корреляции может совпадать с индексом парной корреляции.

Т.о. можно сделать вывод о целесообразности включения в уравнение того или иного фактора.

Индекс множественной корреляциидля уравнениявстандартизованном масштабеможно записать в виде

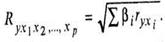
25. Скорректированный коэффициент детерминации.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации.

Коэффициент множественной детерминациирассчитывается как квадрат индекса множественной корреляции:

R²_yx1x2…xp

Множественный коэффициент детерминации (R²), представляющий собой множественный коэффициент корреляции в квадрате, характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель.

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:

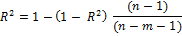
где n – число наблюдений

m – число факторов

26. Частная корреляция.

Как мы отмечали раньше, ранжирование факторов, участвующих во множественной линейной регрессии может быть проведено через стандартизованные коэффициенты регрессии (β-коэффициенты). Эту же цель можно достичь с помощью частных коэффициентов корреляции для линейных связей.

Кроме того, частные показатели корреляции широко используются при отборе фактора. Целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии

(влияние на у фактора х при неизменном уровне других факторов).

В общем виде при наличии p факторов для уравнения

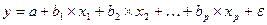
коэффициенты частной корреляции, измеряющие влияние на y фактора xi при неизменном уровне других факторов, можно определить по формуле:

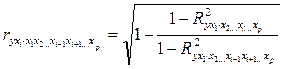
или по рекуррентной формуле:

=

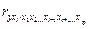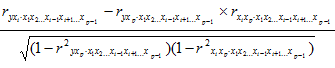
где 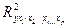- множественный коэффициент детерминации всего комплекса p факторов с результатом;

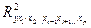- тот же показатель детерминации, но без введения в модель xi.

При i=1 формула коэффициента частной корреляции примет вид:

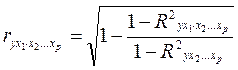Данный коэффициент позволяет измерить тесноту связи между у и х₁ при неизменном уровне всех других факторов, включенных в уравнение регрессии.

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается:

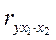- коэффициент частной корреляции 1го порядка

r_yx – нулевого порядка

При двух факторах i=1 данная формула примет вид:

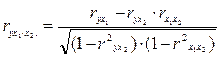Соответственно при i=2 и двух факторах частный коэффициент корреляции у с фактором х₂ можно определить по формуле

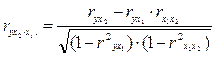Для уравнения регрессии с тремя факторами частные коэффициенты корреляции 2го порядка определяются на основе частных коэффициентов 1го порядка.

28. Предпосылки МНК (Гаусса-Маркова) и последствия их нарушений.
Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.
МНК применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.
МНК позволяет получить такие оценки параметров, при кот. сумма квадратов отклон-й фактич.значений результат. признака от теоретич. минимальна.
- модель д.б. линейной по параметрам
- х - случайная переменная
- значение ошибки – случайны, их изменения не образуют опред.модели (модели остатков)
- число налюденийд.б. больше чисоаоценив.парметров (в 5-6р)
- значения переменной х не д.б. одинаковыми
- совокупность должна быть однородной
- отсутствие взаимосвязи м/у ф-ром х и остатком
- модель регрессии д.б. корректно специфифированна
- в модели не д.б. тесной взаимосвязи м/у фак-ми (ля множ.регрессии)
Основные предпосылки МНК:
n случайный характер остатков
n нулевая средняя остатков, не зависящая от фактора x
n гомоскедастичность (дисперсия каждого отклонения одинакова для всех значений x)
n отсутствие автокорреляции остатков
n остатки должны подчиняться нормальному распределению
p Если регрессионная модель у = a + bх + E удовлетворяет условием Гаусса-Маркова, то оценки а и b, полученные на основе МНК имеют наилучшую дисперсию в классе всех линейных, несмещенных оценок.