Парабола әдісі. (симпсон формуласы)

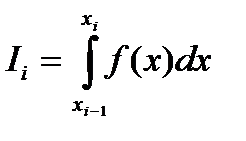интегралын жуықтап есептеу үшін 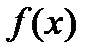функциясын 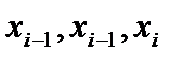нүктелері арқылы тұрғызылған 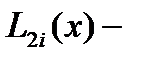Лагранж көп мүшесімен алмастырамыз. Яғни

.

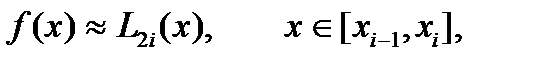
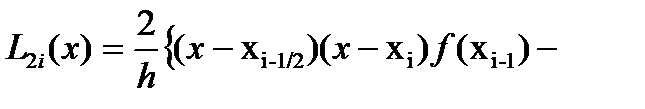
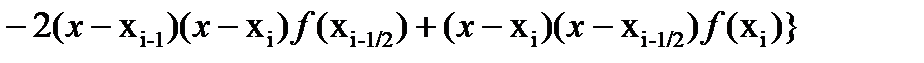Осыдан

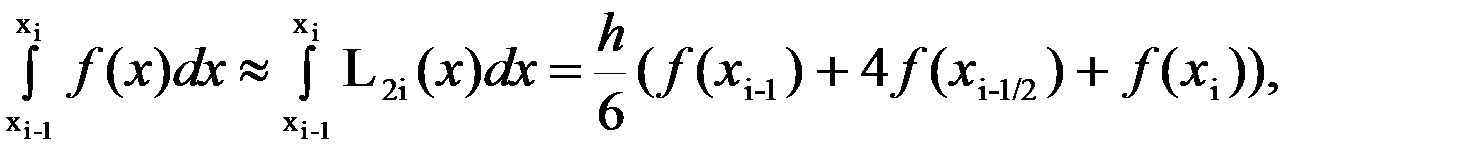
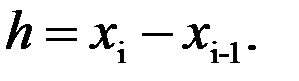
Сонымен мына формуланы –

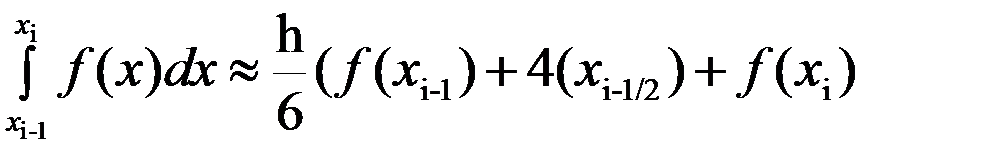
Симпсон немесе парабола формуласы деп атайды.

Бұл формуланың парабола формуласы деп атайтын себебі

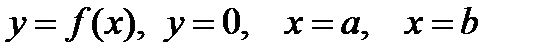сызықтарымен шектелген қисық сызықты трапецияның ауданы 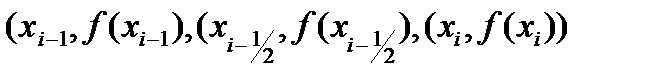нүктелері арқылы өтетін парабола және 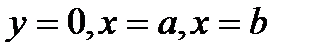түзулерімен шектелген трапецияның ауданымен алмастырылады (4-сурет).

Симпсон формуласы 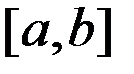кесіндісінде былайша жазылады

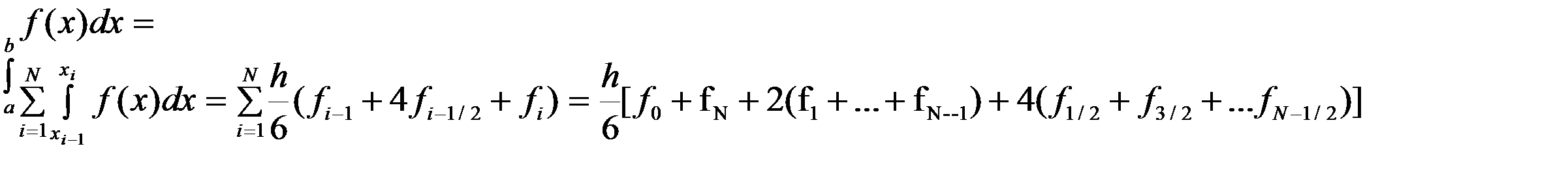
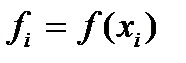
Бөлшекті индекстерден құтылу үшін

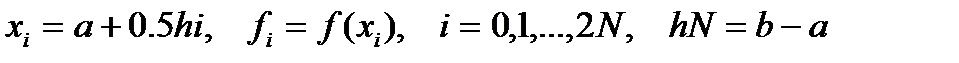десек,онда Симпсон формуласын былайша жазамыз:

.

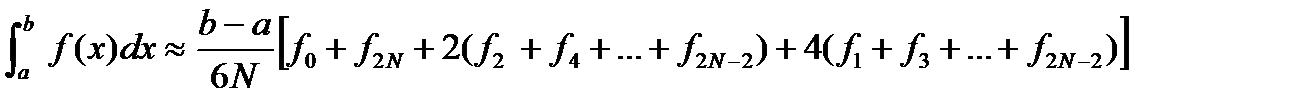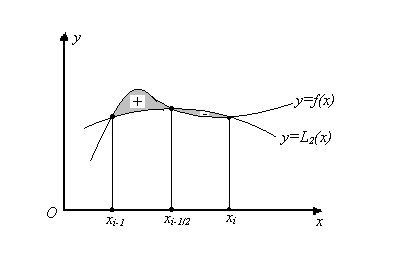
4-сурет

О х у x_i-1 x_i-1/2 x_i y=f(x) y=L₂(x) + -

Симпсон формуласының жіберетін қатесін қарастырардың алдында, оның үш дәрежелі көпмүше үшін дәл екенін көрсетейік. Шынында да

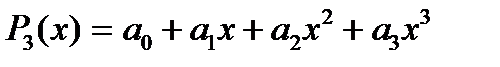болса, онда

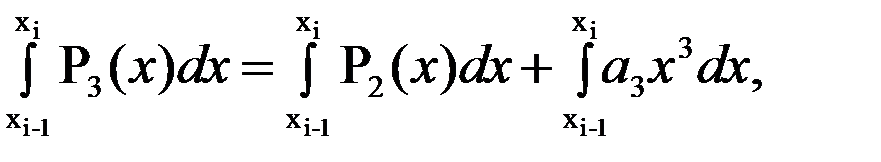
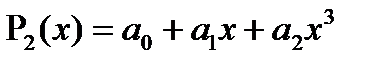
Осыдан

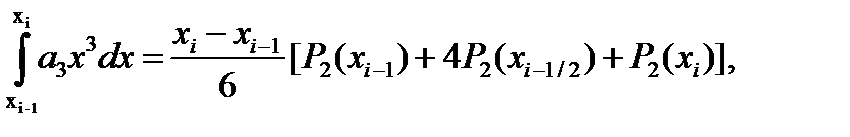
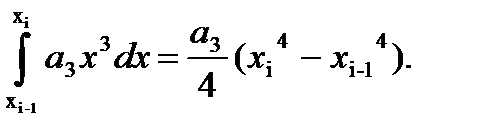
Екіншіден

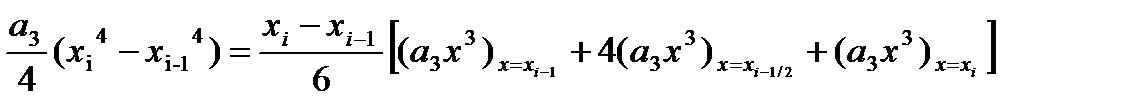
екенін ескерсек

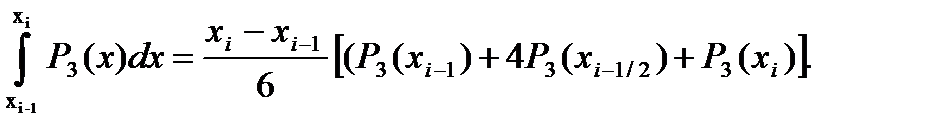
формуласын аламыз.

Сонымен Симпсон формуласының үшінші дәрежеге дейінгі кез келген көпмүшелер үшін дәл екенін көрдік.

Енді Симпсон формуласының қатесін қарастыру үшін мына шарттарды қанағаттандыратын

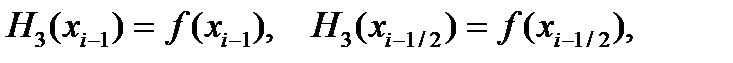
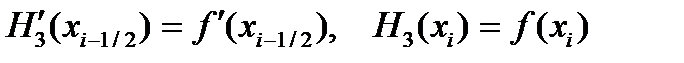
интерполяциялық Эрмит көпмүшелігін пайдаланамыз .

Симпсон формуласы кез келген үш дәрежелі көпмүшеліктер үшін дәл болғандықтан

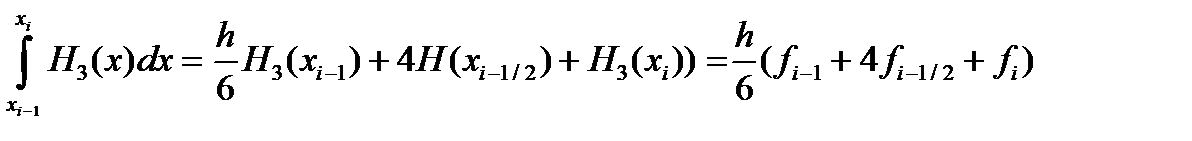
Енді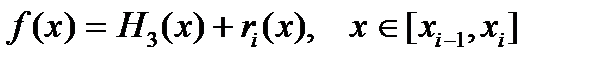

десек,онда

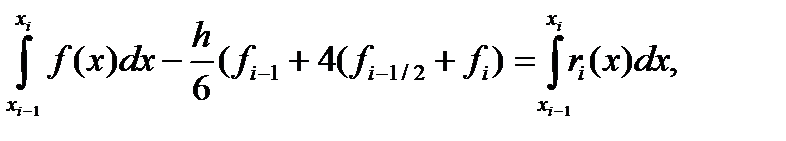
мұндағы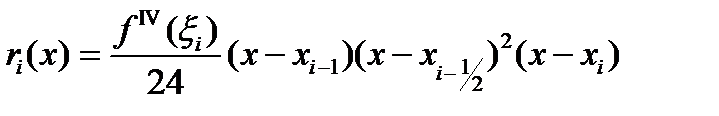

-Эрмит көпмүшесінің жіберетін қатесі.

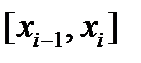кесіндісінде 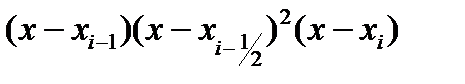көпмүшесі өзінің таңбасын өзгертпейтін болғандықтан

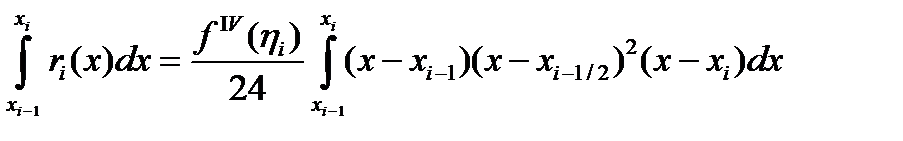
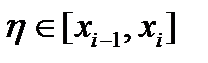
Сондықтан Симпсон формуласының жіберетін қатесi

.

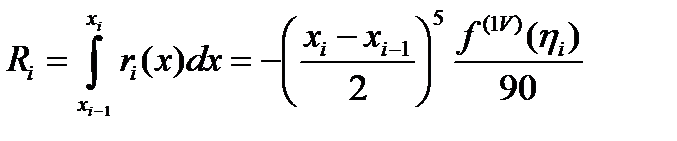Hемесе

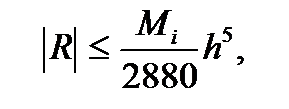
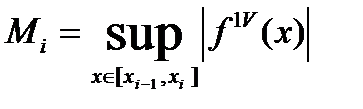
Симпсон формуласының 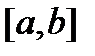кесіндісінде жіберетін қатесі

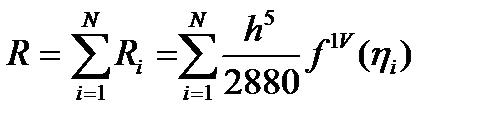
Болғандықтан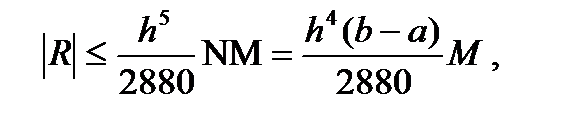

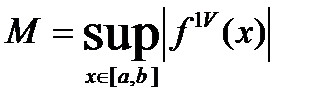
Яғни Симпсон әдісінің 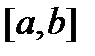кесіндісіндегі дәлдігі .

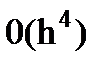16. тор және торлық функциялар

Дифференциалдық тењдеулерді айырымдық ңдістермен шешу – алдымен тор енгізуден басталады. Сондықтан да олар кейде торлық ңдістер деп те аталады. Айырымдық торды тљменде келтірілген мысал арқылы тџсіндірейік.

Айталық, 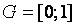аралыѓында мынадай шекаралық есеп берілсін:

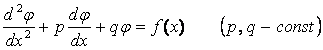, (1.1.1)

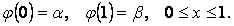(1.1.2)

Бђл есеп бойынша 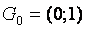аралыѓында (1.1.1) тењдеуін, ал x=0 жңне x=1 болѓанда, (1.1.2) шекаралық шарттарын қанаѓаттандыратын 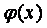функциясын анықтау керек. Осы қойылѓан есеп џшін 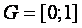аралыѓында айырымдық тор

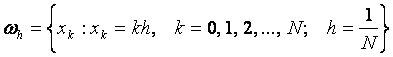
тџрінде енгізіледі. 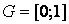аралыѓында бір-бірінен 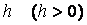қашықтықта жатқан 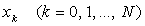нџктелерін айырымдық тордыњ тораптары деп атайды.

Айырымдық тор енгізудіњ нңтижесінде 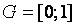аралық тор облысы деп аталатын 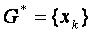нџктелер жиынымен алмастырылады, мђндаѓы 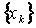– тораптар жиыны. (1.1.1) – (1.1.2) есебініњ 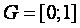облысында анықталѓан дңл шешімі болсын дейік. Онда

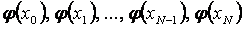(1.1.3)

сандары осы 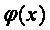функциясыныњ сңйкес

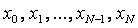
тораптардаѓы мңндері болады. Бђл жаѓдайда (1.1.3) сандар жиыны 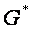облысында анықталѓан торлық функция деп аталады да 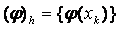арқылы белгіленеді. Ал жоѓарыда айтылѓандай, (1.1.1) – (1.1.2) есебініњ 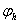жуық шешімі де облысыныњ 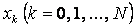тораптарында анықталѓан торлық функция тџрінде анықталады. Ол 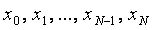нџктелеріне сңйкес келетін 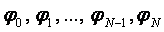сандар жиынынан тђрады жңне 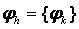деп белгіленеді. Демек, торлық функция џзікті аргументтіњ функциясы, яѓни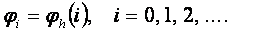

Біз бђл жерде екі торлық функцияны қарастырдық: 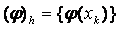– (1.1.1) – (1.1.2) есебініњ 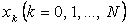тораптарындаѓы дңл шешімі, ал 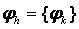– (1.1.1) – (1.1.2) есебініњ 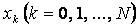тораптарындаѓы жуық шешімі. Жалпы жаѓдайда 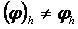, яѓни .

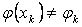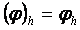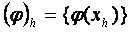Егер N саны жоѓарыдан шектелген болса, онда жңне торлық функцияларын векторлық функциялар деп қарастыруѓа да болады:

.

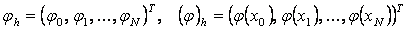Жоѓарыда баяндалѓандай, 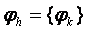– айырымдық тењдеулердіњ шешімі. Ал бђл шешім 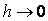жаѓдайда дифференциалдық тењдеулердіњ облысында анықталѓан 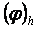дңл шешімінде «жақын» болуы тиіс деген талап – табиѓи нңрсе. Енді осы ђѓымды қандай маѓынада тџсіну керек екендігіне тоқтала кетейік. Ол џшін торлық функцияныњ нормасы деген ђѓым енгіземіз.

Анықтама.Егер 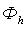торлық функциялар жиынында 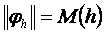сандық функциясы џшін

1. ;

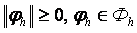2. 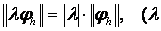– комплекс сан);

3.

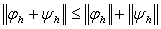
шарттары орындалса, онда 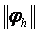шамасы 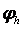торлық функцияныњ нормасы деп аталады жңне 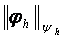арқылы белгіленеді.

Анықтаманыњ аксиомаларын қанаѓаттандыратын норманы ңр тџрлі жолдармен енгізуге болады. Мңселен

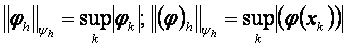(1.1.4)

немесе

(1.1.5)

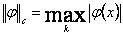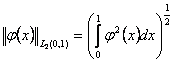Сандық функциялары норма бола алады. Олар функциялар теориясында белгілі жңне нормаларына сңйкес келеді.

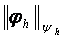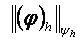Бђдан ары жңне нормалары (1.1.4) тџрінде енгізілген деп есептейміз.

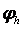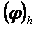Норма анықталѓаннан кейін жңне торлық функциялардыњ бір-біріне «жақындыѓын» 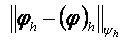нормасыныњ шамасына қарай баѓалаймыз.

17. Эйлер әдісінің модификациялары.(20)

Модифицированный метод Эйлера за счет незначительного увеличения времени вычислений позволяет добиться большей точности вычислений. Этот метод отличается от метода Эйлера тем, что в нем для повышения точности определения значений зависимой переменной применяется процесс итераций.

Хотя модифицированный метод Эйлера приводит к накоплению меньшей ошибки, чем метод Эйлера, но при достаточно большом числе шагов по X ошибка все же может оказаться существенной.

Процедура модифицированного метода Эйлера ( рис. 78, а) строится на основе вычисления касательной к интегральной кривой в средней точке отрезка интегрирования. Значение z / n 1 получается на конце отрезка прямой, параллельной этой касательной и проведенной через точку с координатами tn, уп. Для исправленного метода Эйлера ( рис. 78, б) точка уп 1 лежит на биссектрисе угла, образованного касательными к интегральной кривой в начале и конце отрезка интегрирования.

В модифицированном методе Эйлера существует два типа ошибок: 1) обусловленные линейной апроксимацией и 2) являющиеся результатом накопления ошибок, возникших при вычислении во всех предыдущих точках. Величина этих ошибок до некоторой степени может меняться при соответствующем выборе максимально допустимой разности между двумя последними апроксимациями. Это уменьшение отдельных ошибок приводит к снижению погрешности вычислений в целом.

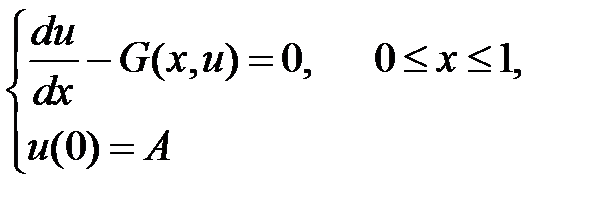(1)

есебін қарастырайық. 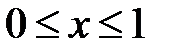кесіндісінде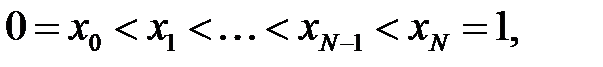

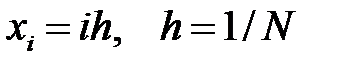нүктелер жиынын (торды) алайық. 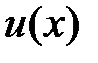шешімі мәндерінінің жуық 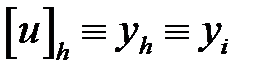шешімінің айырымдылық схемасын жоғарыда алынған торда құрайық:

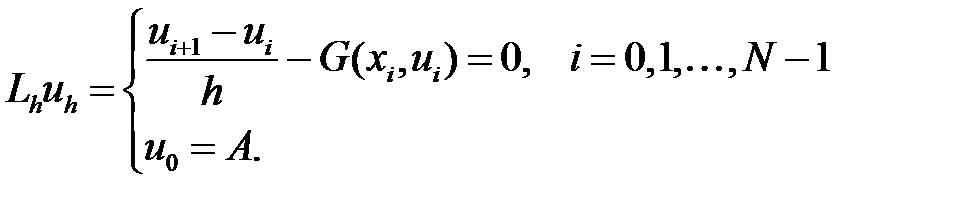(2)

Бұл схеманың аппроксимация (жуықтау) реті (жуықтау дәлдігі) 1-ге тең. Егер 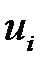есептелсе, онда

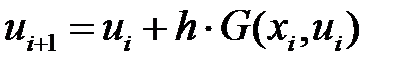(3)

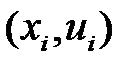нүктесін 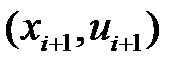нүктесіне, 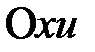жазықтығында 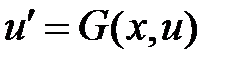дифференциалдық теңдеуінің, 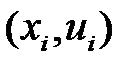нүктесінен өтетін, 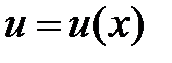интегральдық қисығына жанама бойымен жылжытуы.

Осы айтылған әдіс – Эйлер әдісі деп аталады.

Егер 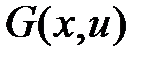функциясы 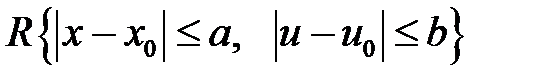тікбұрышында Липшиц шартын қанағаттандырса, яғни 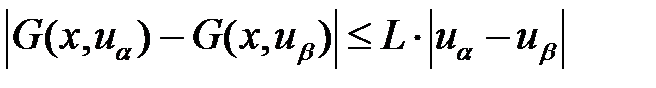, 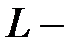тұрақты шама және 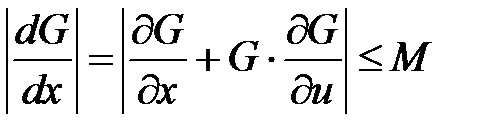теңсіздігі орындалса, 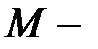тұрақты шама, онда шешімінің қателігінің бағасы төмендегідей болады

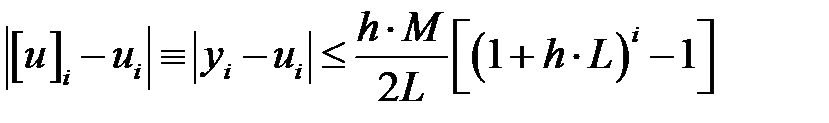. (4)

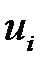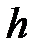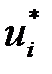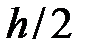Ал, іс жүзінде, алдымен -ді қадамымен және -ді қадамымен есептейді де қателігінің бағасын былай анықтайды:

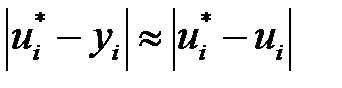. (5)