Связь между векторами и
В случае изотропных диэлектриков вектор поляризации 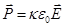 . Подставив это соотношение в (10), получим
. Подставив это соотношение в (10), получим 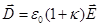 , или
, или
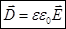 . (12)
. (12)
Из формулы (12) видно, что в изотропных диэлектриках вектор 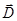 коллинеарен вектору
коллинеарен вектору 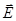 . В анизотропных же диэлектриках эти векторы, вообще говоря, не коллинеарны.
. В анизотропных же диэлектриках эти векторы, вообще говоря, не коллинеарны.
Поле вектора 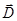 наглядно можно изобразить с помощью линий вектора
наглядно можно изобразить с помощью линий вектора 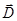 , направление и густота которых определяются точно так же, как и для линий вектора
, направление и густота которых определяются точно так же, как и для линий вектора 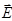 . Линии вектора
. Линии вектора 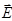 могут начинаться и заканчиваться как на сторонних, так и на связанных зарядах; мы говорим, что источниками и стоками поля являются любые заряды. Источниками же и стоками поля вектора
могут начинаться и заканчиваться как на сторонних, так и на связанных зарядах; мы говорим, что источниками и стоками поля являются любые заряды. Источниками же и стоками поля вектора 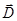 являются только сторонние заряды: только на них могут начинаться и заканчиваться линии вектора
являются только сторонние заряды: только на них могут начинаться и заканчиваться линии вектора 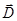 . Через области поля, где находятся связанные заряды, линии вектора
. Через области поля, где находятся связанные заряды, линии вектора 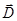 проходят не прерываясь.
проходят не прерываясь.
