Метод разложение числителя

Интегрирование некоторых дробей.Методы и приёмы решения

На данном уроке мы научимся находить интегралы от некоторых видов дробей. Для успешного усвоения материала Вам должны быть хорошо понятны выкладки статейНеопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.

Как я уже отмечал, в интегральном исчислении нет удобной формулы для интегрирования дроби 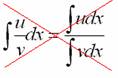. И поэтому наблюдается грустная тенденция: чем «навороченнее» дробь, тем труднее найти от нее интеграл. В этой связи приходится прибегать к различным хитростям, о которых я сейчас и расскажу.

Метод разложение числителя

Пример 1

Найти неопределенный интеграл. Выполнить проверку.

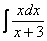
На уроке Неопределенный интеграл. Примеры решениймы избавлялись от произведения функций в подынтегральном выражении, превращая её в сумму, удобную для интегрирования. Оказывается, что иногда в сумму (разность) можно превратить и дробь!

Анализируя подынтегральную функцию, мы замечаем, что и в числителе и в знаменателе у нас находятся многочлены первой степени: 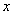и .

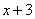Когда в числителе и знаменателе находятся многочлены одинаковой степени, то помогает следующий искусственный приём: в числителе мы должны самостоятельно организовать такое же выражение, что и в знаменателе:

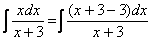
Рассуждение может быть следующим: «В числителе мне надо организовать 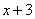, но если я прибавлю к «иксу» тройку, то, для того, чтобы выражение не изменилось – я обязан эту же тройку и вычесть».

Теперь можно почленно разделить числитель на знаменатель:

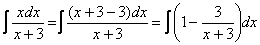
В результате мы добились, чего и хотели. Используем первые два правила интегрирования:

Готово. Проверку при желании выполните самостоятельно.

Обратите внимание, что 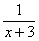во втором интеграле – это «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.

Кстати, рассмотренный интеграл можно решить и методом замены переменной, обозначая 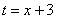, но запись решения получится значительно длиннее

Пример 2

Найти неопределенный интеграл. Выполнить проверку.

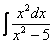
Это пример для самостоятельного решения. Следует заметить, что здесь метод замены переменной уже не пройдёт.

Внимание, важно! Примеры №№1,2 являются типовыми и встречаются часто. В том числе, подобные интегралы нередко возникают в ходе решения других интегралов, в частности, при интегрировании иррациональных функций (корней).

Рассмотренный приём работает и в случае, если старшая степень числителя, больше старшей степени знаменателя.

Пример 3

Найти неопределенный интеграл. Выполнить проверку.

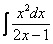
Начинаем подбирать числитель.

Алгоритм подбора числителя примерно такой:

1) В числителе мне нужно организовать 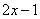, но там 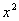. Что делать? Заключаю 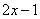в скобки и умножаю на : .

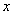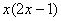2) Теперь пробую раскрыть эти скобки, что получится? 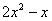. Хмм… уже лучше, но никакой двойки при 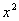изначально в числителе нет. Что делать? Нужно домножить на :

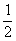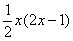
3) Снова раскрываю скобки: 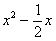. А вот и первый успех! Нужный 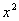получился! Но проблема в том, что появилось лишнее слагаемое 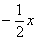. Что делать? Чтобы выражение не изменилось, я обязан прибавить к своей конструкции это же :
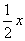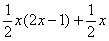. Жить стало легче. А нельзя ли еще раз в числителе организовать ?

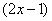4) Можно. Пробуем: 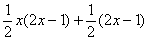. Раскрываем скобки второго слагаемого:
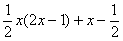. Простите, но у меня вообще-то было на предыдущем шаге 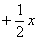, а не 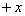. Что делать? Нужно домножить второе слагаемое на :

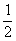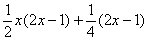
5) Снова для проверки раскрываю скобки во втором слагаемом:
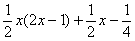. Вот теперь нормально: получено 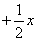из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое 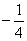, значит, я обязан прибавить к своему выражению :

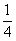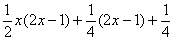
Если всё выполнено правильно, то при раскрытии всех скобок у нас должен получиться исходный числитель подынтегральной функции. Проверяем:
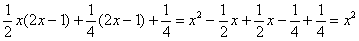Гуд.

Таким образом:

Готово. В последнем слагаемом я применил метод подведения функции под дифференциал.

Если найти производную от ответа и привести выражение к общему знаменателю, то у нас получится в точности исходная подынтегральная функция 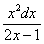. Рассмотренный метод разложения 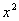в сумму – есть ни что иное, как обратное действие к приведению выражения к общему знаменателю.

Алгоритм подбора числителя в подобных примерах лучше выполнять на черновике. При некоторых навыках будет получаться и мысленно. Припоминаю рекордный случай, когда я выполнял подбор для 11-ой степени, и разложение числителя заняло почти две строчки Вёрда.

Помимо алгоритма подбора можно использовать деление столбиком многочлена на многочлен, но, боюсь, объяснения займут еще больше места, поэтому как-нибудь в другой раз.

Пример 4

Найти неопределенный интеграл. Выполнить проверку.

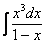
Это пример для самостоятельного решения.