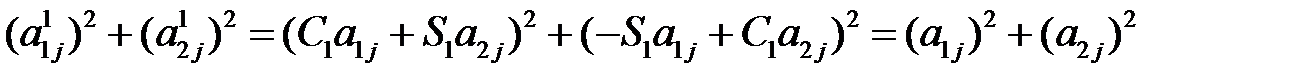Разложение симметричных матриц. Метод квадр. корней решения лин. алг.систем

Пусть A=[a_ij]_n×n данная симметричная матрица a_ij=a_ji. Будем строить разложение матрицы А в виде А=U^TU (1), где U- верхняя (правая) треугольная матрица. Равенство (1) перепишем в подробной форме:

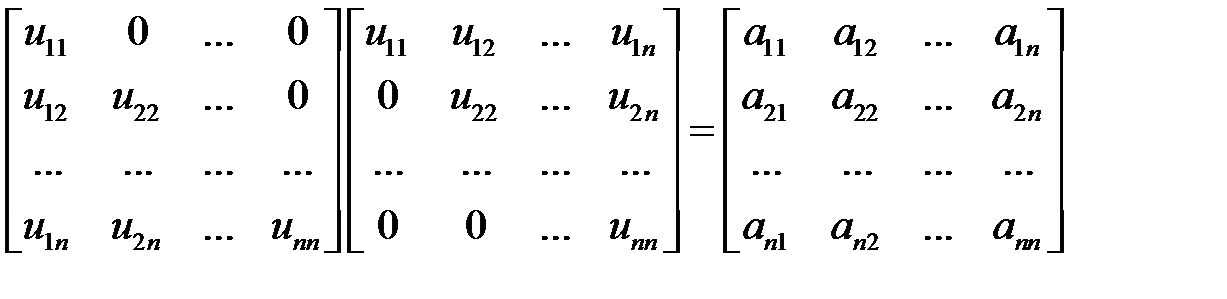(2)

Перемножив (2) и учитывая симметричность матрицы А, получаем сист. ур. относительно неизвестных u_ij:

u₁₁²= a₁₁ u₁₂u₁₁=a_{12 ………} u_1nu₁₁=a_1n

u₁₂²+ u₂₂²=a_{22 ……..} u_1nu₁₂+u_2nu₂₂=a_2n (3)

. . . . . . . . . . . . . . . . . . . . . . .

u_1n²+u_2n²+…+u_nn²=a_nn

Cист. (3) решаем след. образом, в начале находим элемент u₁₁= 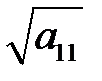, далее из остальной части 1-ой строки находим 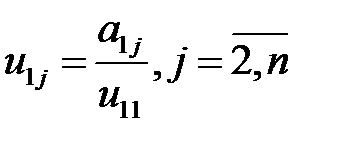. Из 1-го ур. во 2-ой строке находим 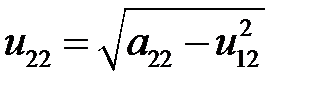. Из остальной части 2-ой строки находим: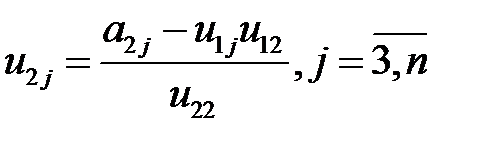

Продолжая, последним находим элемент: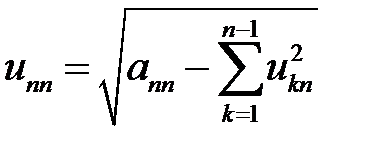

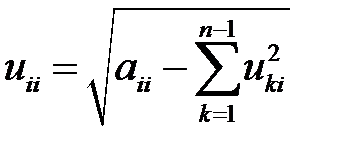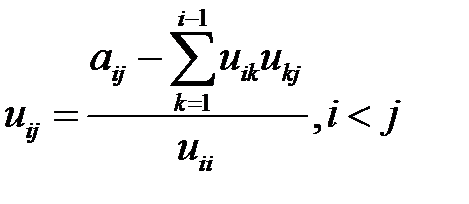, указанный процесс можно описать след. форм.: (4) (5)

При практическом счёте необходимо своевременно переключаться с форм. (4) на (5), и наоборот.

Замечание. Более универсально, чем разложение (1) явл. разложение эрмитовых матриц: А=U^*ΔU, где Δ-диагональная матрица на главной диагонали, которой стоят числа ±1.

Замечание: Реализацию вычисления по форм. (4), (5) могут помешать 2 обстоятельства:

- отрицательное подкоренное выражение в (4);

- обращение в 0 знаменателя (5).

Однако, если матрица А симметрична, положительно определённая, то разложение (1) всегда осуществляеться тоже самое отномительно к матрицам с диагоналями преобладанием.

Применим разложение (1) к решению лин. алг. сист. Ах=b (6) с симметрично положительно определённой матрицей А. В силу (1) имеем:U^TUx=b (7)

Перепишем (7) в виде 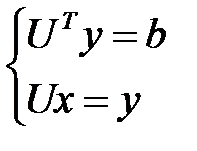(8)

Очевидно, что решение подсист. (8) не сложнее, чем обратный ход метода Гаусса.

30. Метод вращения решений лин. алг. сист.

Рассм. метод вращений решения лин. алг. сист. не допуская большого роста абсолютных велечин элем. матрицы сист.. Пусть задана сист.: 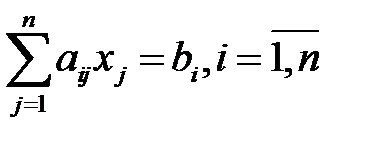(1)

Возьмём 2 числа С₁ и S₁ умножим 1-ое ур. сист. на С₁ , 2-ое на S₁. Полученные ур. сложим и заменим этим ур. 1-ое ур. сист., т.е. 1-ое ур. сист. будет иметь вид: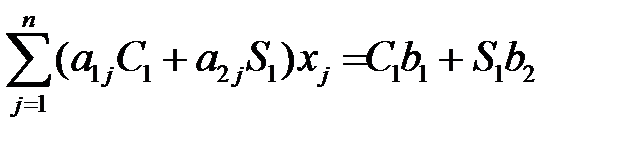

Далее 1-ое ур. сист. умножим на (-S₁), а 2-ое умножим на С₁, сложив, получим ур. и заменим 2-ое ур. в 1, т.е. 2-ое ур. в 1 будет иметь вид: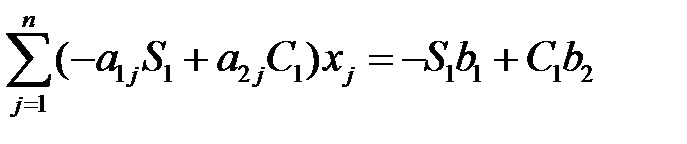

Перейдём к выбору чисел С₁ и S₁, выберем их т. о., чтобы коэфф. при х₁ во 2-ом ур. получилась сист. =0, т.е. чтобы выполнялось усл.: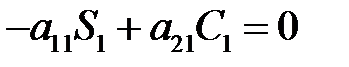

также потребуем, чтобы имело место усл. нормировки: 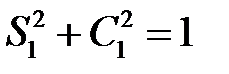. Тогда можно положить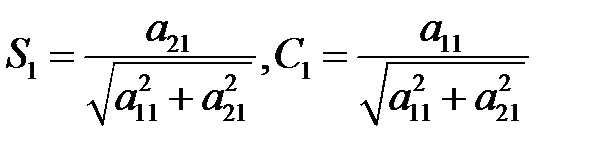

После указанного преобр. сист. (1) имеет вид:

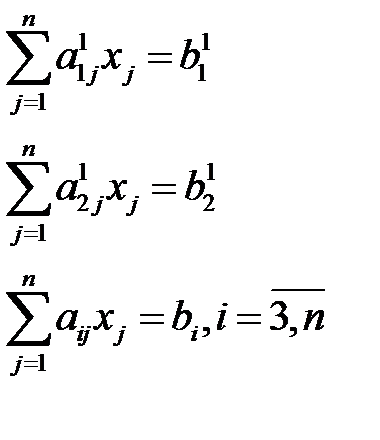(2)

Заметим, что числа С₁ и S₁ можно трактовать, как sin и cos некоторого угла, поэтому очевидно, что переход от (1) к (2) представляет собой преобраз. вращения с некоторой ортогональной матрицей.

Предположим преобразуем исходную сист., 1-ое и 3-ее ур. в (2) и проведя те же рассуждения. Исключим из 3-го ур. в (2) перемножая x₁, далее берём 1-ое и 4-ое ур. получаем сист., 1-ое и 5-ое, и т.д. 1-ое и n-ое. Т. о. после указанных шагов сист. (2) преобразуется к виду:

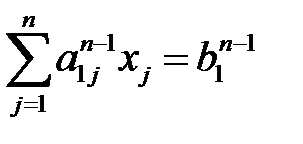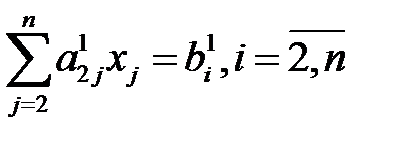(3), (4)

Далее обрабатывая подсист. (4). Проведя аналогичные рассуждения для подсист. (4) исключим неизвестную х₂ из всех ур. подсист. (4) начинаю со 2-го и т.д. продолжаем указанный процесс до тех пор, пока сист. (3), (4) не будет иметь треугольную матрицу, т.е. не будет приведена к виду: 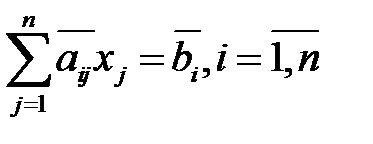(5)

Теперь нахождение неизвестных из сист. (5) аналогично обратному ходу метода Гаусса.

Преимущество этого метода заключается в том, что при переходе от сист. (1) к сист. (5) евклидова норма каждого столбца матрицы неизменяется. Действительно после 1-го шага имеем: