П.3. Линейные оболочки и линейная зависимость

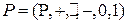- поле скаляров, 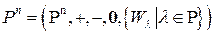- арифметическое 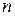- мерное векторное пространство, где 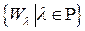- множество операций умножения на скаляр, .

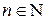Определение. Множество всех линейных комбинаций 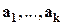с коэффициентами из 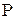называется линейной оболочкой векторов 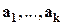; обозначается .

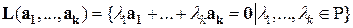Пример 1. ;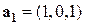

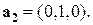
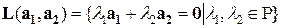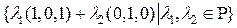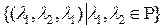= = -множество 3-мерных векторов, у которых первая и последняя компоненты совпадают.

Пример 2. Рассмотрим систему единичных 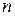- мерных векторов. ,

= .

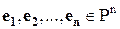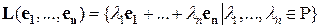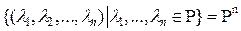Определение. Линейная оболочка пустой системы векторов состоит из одного нулевого вектора.

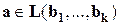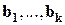
Теорема 1. Если ; 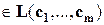, то .

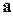
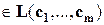Доказательство.

Если 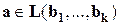т.е. 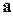-линейная комбинация векторов 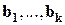; а каждый 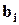, 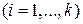-линейная комбинация векторов 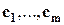, то 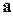-линейная комбинация векторов 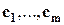, т.е. .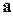

■

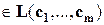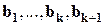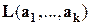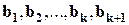Теорема 2.Если принадлежат линейной оболочке , то -линейно зависимая система векторов.

Другими словами, любые 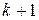вектора, принадлежащие линейной оболочке из 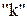векторов, - линейно зависимы.

Доказательство.

1) Если хотя бы один из векторов 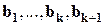равен 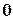, то система линейно зависима, (из свойства 1).

2) Пусть 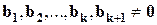. Для доказательства теоремы применим метод математической индукции.

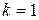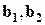
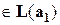
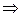
i) , 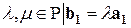; 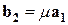, 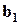и 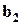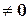, поэтому .

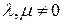Рассмотрим линейную комбинацию:

.

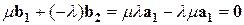Линейная комбинация равна нулю, а не все скаляры равны нулю, поэтому 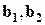- линейно зависимая система векторов.

ii) Предположим, что утверждение доказано для числа 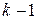, т.е. любые 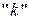векторов, принадлежащие линейной оболочке от 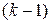вектора линейно зависимы.

iii) Докажем утверждение теоремы для числа .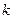

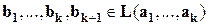, тогда существуют 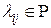, такие, что

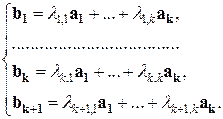(1)

1) Если в этой системе все коэффициенты при векторе 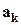равны 0, т.е. 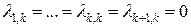, то 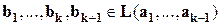; по индукционному предположению 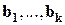- линейно зависимая система векторов. Тогда 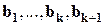- линейно зависимая система векторов по свойству 2.

2) Пусть хотя бы один из коэффициентов при векторе 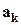не равен нулю, т.е. среди чисел 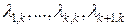есть ненулевые.

Пусть 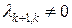. Из последнего равенства системы (1) имеем:

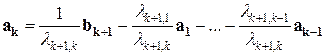, то есть 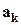- линейная комбинация векторов .

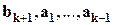Заменим в первых « 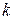» равенствах системы (1) вектор 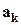полученным выражением:

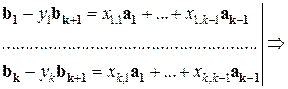
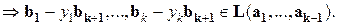
По индукционному предположению, векторы: 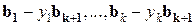- линейно зависимы. Тогда существуют 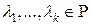, такие, что 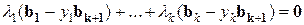и не все 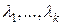равны 0.

.

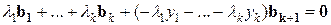Скаляры 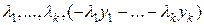не все равны 0, поэтому 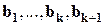- линейно зависимая система векторов.

По методу математической индукции теорема доказана для всех .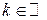

■

Следствие 1.Пусть 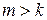и 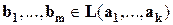, тогда 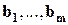-линейно зависимая система векторов.

Следствие 2. Пусть 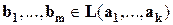и 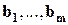-линейно независимая система векторов, тогда .

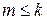Следствие 3.В 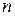- мерном арифметическом пространстве любая система векторов, содержащая более 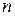векторов, линейно зависима.

Доказательство.

Пусть 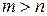, 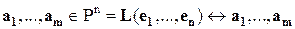- линейно зависимая система векторов.

■

Пример. , , , .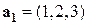

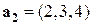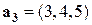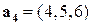Векторы линейно зависимы в .