Линейные оболочки и подпространства
Определение. Подпространством 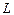 линейного пространства
линейного пространства 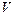 называется множество векторов из
называется множество векторов из 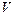 такое, что для любых двух векторов
такое, что для любых двух векторов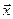 и
и 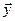 из
из 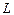 и любых двух вещественных чисел
и любых двух вещественных чисел 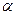 и
и 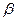 линейная комбинация
линейная комбинация 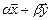 также принадлежит
также принадлежит 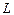 .
.
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 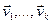 называется множество всех линейных комбинаций векторов
называется множество всех линейных комбинаций векторов 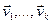 . Обозначается
. Обозначается 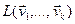 .
.
Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств 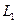 и
и 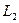 называется множество всех векторов
называется множество всех векторов 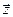 , представимых в виде
, представимых в виде 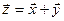 , где
, где 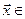
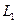 ,
, 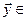
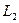 . Обозначается
. Обозначается 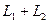 .
.
Утверждение. Сумма и пересечение подпространств 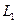 и
и 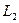 являются линейными пространствами, и их размерности связаны равенством
являются линейными пространствами, и их размерности связаны равенством
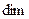
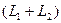 +
+ 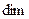
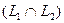 =
= 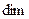
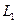 +
+ 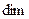
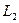 .
.
Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами 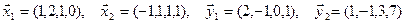 .
.
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства 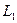 , порождённого векторами
, порождённого векторами 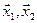 , равенство нулю линейной комбинации
, равенство нулю линейной комбинации 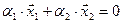 , эквивалентное системе уравнений
, эквивалентное системе уравнений 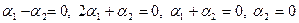 , достигается лишь при условии
, достигается лишь при условии 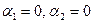 . Следовательно, векторы
. Следовательно, векторы 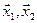 линейно
линейно
независимы и размерность подпространства 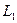 равна 2:
равна 2: 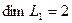 . Для подпространства
. Для подпространства 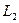 , порождённого векторами
, порождённого векторами 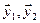 , проводя аналогичный анализ, получим
, проводя аналогичный анализ, получим 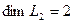 .
.
Вычислим теперь размерность пересечения подпространств 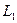 и
и 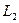 . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор
. По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор 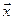 подпространства
подпространства 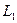 является линейной комбинацией базисных векторов
является линейной комбинацией базисных векторов 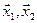 :
: 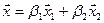 . Аналогично для подпространства
. Аналогично для подпространства 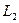 имеем
имеем 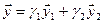 , тогда условие принадлежности пересечению есть
, тогда условие принадлежности пересечению есть 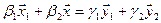 или
или 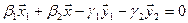 .
.
 Это условие представляет собой систему уравнений относительно коэффициентов
Это условие представляет собой систему уравнений относительно коэффициентов 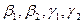 . Составим матрицу системы и упростим её с помощью элементарных преобразований:
. Составим матрицу системы и упростим её с помощью элементарных преобразований: 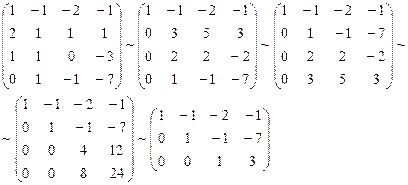
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим 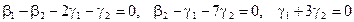 ,
,
откуда 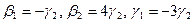 .
.
Полагая свободное неизвестное 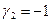 , для остальных имеем
, для остальных имеем
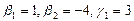 . Итак, пересечение подпространств
. Итак, пересечение подпространств 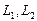 имеет один базисный вектор
имеет один базисный вектор
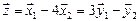 .
.
Размерность пересечения 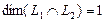 . Следовательно, в соответствии с равенством
. Следовательно, в соответствии с равенством
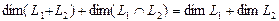

размерность суммы подпространств 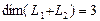 . В качестве базиса суммы подпространств можно взять, например, векторы
. В качестве базиса суммы подпространств можно взять, например, векторы 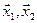 , дополненные вектором
, дополненные вектором 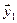 . В линейной независимости векторов
. В линейной независимости векторов 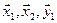 убедиться нетрудно.
убедиться нетрудно.
Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами 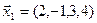 ,
, 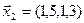 ,
, 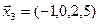 ,
, 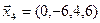 ,
, 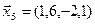 .
.
3.40. Найти размерность и какой-либо базис линейной оболочки векторов 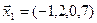 ,
, 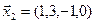 ,
, 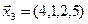 ,
, 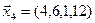 ,
, 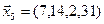 .
.
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R2;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 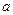 последовательностей в пространстве сходящихся последовательностей;
последовательностей в пространстве сходящихся последовательностей;
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале 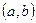 функций в пространстве функций, непрерывных на отрезке
функций в пространстве функций, непрерывных на отрезке 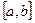 .
.
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R3;
б) векторов из пространства Rn, координаты которых удовлетворяют уравнению 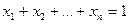 ;
;
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве 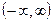 функций в пространстве функций, ограниченных на том же множестве.
функций в пространстве функций, ограниченных на том же множестве.
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а) 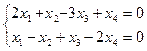 ; б)
; б) 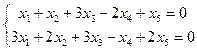 ;
;
в) 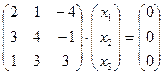 .
.
3.44. Доказать, что данное множество является подпространством в Rn, найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению 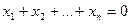 ;
;
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами 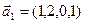 ,
, 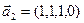 и
и 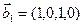 ,
, 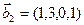 . Является ли эта сумма прямой суммой?
. Является ли эта сумма прямой суммой?
3.46. Найти размерность суммы и пересечения линейных оболочек векторов 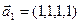 ,
, 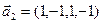 ,
, 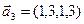 и
и 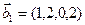 ,
, 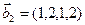 ,
, 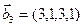 . Является ли их cумма прямой?
. Является ли их cумма прямой?
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 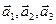 и
и 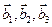 , если
, если
а) 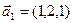 ,
, 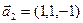 ,
, 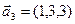 ,
, 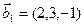 ,
, 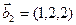 ,
, 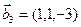 ;
;
б) 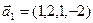 ,
, 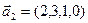 ,
, 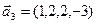 ,
, 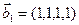 ,
, 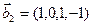 ,
, 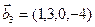 .
.
3.48. Найти базис суммы и пересечения линейных оболочек 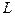
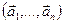 и
и 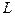
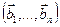 , если
, если
а) 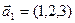 ,
, 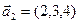 ,
, 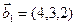 ,
, 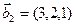 ;
;
б) 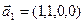 ,
, 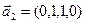 ,
, 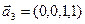 ,
, 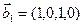 ,
, 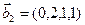 ,
, 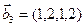 .
.
Является ли прямой сумма этих подпространств?
