В41.Теорема о единственности мгновенного центра скоростей при плоском непоступательном движении среды

Движения вырожденной двумерной твердой среды, при котором все точки среды во время движения находятся в одной плоскости называется плоским.

ТЕОРЕМА:При любом движении плоской среды (кроме поступательного) в каждое мгновение существует единственная точка, скорость которой равна нулю (мгновенный центр скоростей), а скорости всех остальных точек распределены так, как если бы среда в это мгновение вращалась вокруг мгновенного центра скоростей.

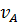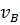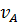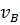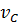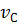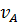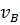Д о к а з а т е л ь с т в о . Рассмотрим две движущиеся точки плоской среды А и В, предположив сначала, что их скорости и не параллельны. Проведем в точках А и В прямые, перпендикулярные и соответственно, и рассмотрим точку С их пересечения. Пусть — скорость этой точки среды. Проекции на указанные прямые должны быть равны проекциям на эти прямые и соответственно, а они равны нулю, так как прямые перпендикулярны 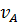и 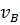. Значит, скорость 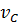должна иметь нулевые проекции на две непараллельные прямые, что возможно лишь в том случае, когда эта скорость равна нулю. Точка С —единственная точка, скорость которой равна нулю, ибо в противном случае была бы неподвижна вся плоская среда, а мы предположили, что точки А и В движутся, т.е. что их скорости отличны от нуля.

При наличии точки С, скорость которой равна нулю, движущаяся плоская среда может лишь вращаться вокруг С. Угловая скорость этого вращения равна 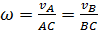, где АС и ВС — расстояния от А и В до С. Скорость любой другой точки среды, например D, равна 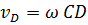, где CD — расстояние от C до D.

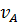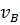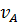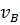Пусть теперь и параллельны. Если они равны, т.е. если в среде есть две точки с одинаковыми скоростями, то и все остальные точки среды имеют ту же скорость, т.е. движение поступательно, а условием доказываемой теоремы этот случай исключен. Случай же, когда и параллельны, но не равны, возможен лишь тогда, когда точки А и В расположены на прямой, перпендикулярно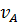й и 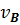так как в противном случае проекции этих скоростей на прямую, соединяющую А и В, не были бы равны. Соединим концы векторов 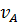и 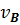прямой и найдем точку С ее пересечения с прямой АВ. Взяв в качестве точки O′ точку А имеем 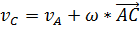, или, учитывая, что движение плоское, скорости параллельны 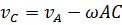. Аналогично 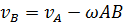, откуда 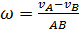, а по построению 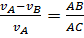, так что 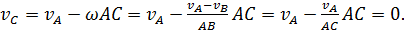Теорема доказана.

42. Движение ракеты. Формула Циолковского. Благодаря горению топлива внутри ракеты развиваются большие давления, и продукты горения вылетают из сопла наружу. Ракету можно было бы рассматривать как систему постоянного состава, но тогда наряду с самой ракетой нужно было бы все время рассматривать и вытекшее ранее «облако» газа. К системе «ракета + вытекшие газы» могут быть применены теоремы механики. В частности, если рассматривать движение ракеты при отсутствии внешних сил, то ракета и вытекшие из нее газы представляют собой замкнутую материальную систему и, следовательно, скорость центра инерции этой системы не может меняться. Поэтому из того факта, что газы под действием внутренних сил вытекают, скажем, влево, следует сразу, что корпус ракеты должен двигаться вправо.

Рассмотрим движение ракеты на активном прямолинейном участке траектории. В качестве объема W рассмотрим объем, ограниченный внешней оболочкой корпуса ракеты и срезом сопла. Предположим, что процесс горения топлива протекает достаточно медленно и что поэтому на интересующем нас интервале времени скорость движения центра инерции масс, расположенных внутри ракеты, относительно ее корпуса пренебрежимо мала по сравнению со скоростью самой ракеты. Рассматривая разгон ракеты на прямолинейном активном участке траектории, пренебрежем вращением ракеты относительно собственных осей, т.е. предположим, что ракета движется поступательно.

Как известно, для любой системы переменного состава дополнительная сила действующая на такую систему

Rдоп = – fуход + fприх . (1)

где fуход и fприх обозначают соответственно пределы

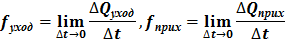
Здесь ΔQуход — количество движения частиц, уходящих из заданного объема за время Δt; соответственно ΔQприх — количество движения частиц, приходящих за время Δt в заданный объем извне.

Для случая стационарного потока частиц, т.е. случая когда суммарный расход массы (поступающей в объем и уходящей из него) равен нулю, выражение (1) принимает вид Rдоп = μприх vприх – μуход vуход , (2)

где

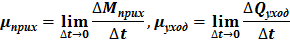
соостветственно скорость прихода и ухода массы.

Условия внутри корпуса ракеты заведомо нестационарны хотя бы потому, что для ракеты fприх = 0, а fуход ≠ 0. Однако в интервале времени, малом по сравнению с периодом сгорания всего топлива, можно считать условия внутри ракеты мало отличающимися от стационарных (это утверждение называют «гипотезой квазистационарности»). Приняв эту гипотезу, можно воспользоваться формулой (2). Для ракеты Rдоп = – μvуход , где vуход — скорость газов, вылетающих из сопла, относительно корпуса ракеты, а μ = μуход = – dМ/dt, так что 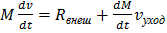(3)

Это уравнение называется уравнением Мещерского. Оно описывает поступательное движение ракеты на прямолинейном активном участке траектории.

Если разгон ракеты происходит в условиях, когда можно пренебречь воздействием на нее внешних сил (например, вдали от каких-либо центров тяготения и вне атмосферных оболочек), и если vуход = const = и, то формулу (3) можно переписать так:

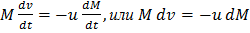
43. Основные свойства, методы и события формы.Форма — это главный компонент приложения, который, как и менее значительные компоненты, имеет св-ва. При создании новой формы среда Delphi сама задает начальные значения свойствам формы, кот. можно изменить так, как нужно. Размеры и положение формы определяют с помощью свойств Width и Height, а местоположение - с помощью свойств Left и Top (значения задаются в пикселах). С помощью св-ва Position можно организовать автоматическое размещение формы на экране: poDefault - размеры и положение формы подбираются автоматически исходя из размеров экрана; poDefaultPosOnly - положение - автоматически, а ширина и высота – знач-ми св-в Width и Height; poDefaultSizeOnly – размеры - автоматически, а местоположение – знач-ми св-в Left и Top; poDesigned - размеры и положение – знач-ми св-в Left, Top, Width, Height; poDesktopCenter - форма в центре рабочего стола размеры – знач-ми Width и Height; poScreenCenter - форма размещается в центре экрана,размеры –знач-ми св-в Width и Height. Для сворачивания формы или разворота ее на всю рабочую область экрана с помощью соответствующих кнопок рамки определяется свойством WindowState: wsNormal - нормальное состояние; wsMinimized - форма свернута; wsMaximized - форма развернута на весь экран. Главное свойство, с кот. начинается настройка формы — св-во Name. Оно содержит идентификатор, используемый для обращения к форме из программы. По умолчанию назначается имя Form1. Св-во Name редактируется в окне Object Inspector. Заголовок задается в свойстве Caption. Главная форма — это форма, кот.показывается при запуске программы.Она м.б. только одна, а у нее неограниченное число подчиненных форм, вспомогательных окон. Если закрывается главная форма,то завершается и работа всего приложения. Есть два типа форм – создаваемые автоматически (AutoCreate form) и создаваемые вручную. По умолчанию создаются формы первого типа. Автоформы: Такие формы удобны тем, что к моменту запуска программы все заданные формы созданы и к ним можно смело обращаться. Создание свободной формы: 1.можно просто открыть окно настроек проекта на вкладке Forms (меню Project – Options). Там два списка(правый – находятся свободные формы,а слева - автоматически создаваемые. Кликнем дважды мышкой по имени нашей формы, которое скорее всего будет называться AboutForm она переместится в список справа). 2. ручная правка файла проекта – нужно просто удалить строку в которой эта самая форма создаётся. Модальные формы отличаются от других форм тем, что при выводе ее на экран, доступ к родительской форме, а так же к ранее созданным объектам приложения запрещается до момента закрытия модальной формы. Для того чтобы показать на экране ранее созданную подчиненную форму, можно применить следующий метод: Имя_формы.ShowModal(вызывает форму в модальном режиме). Модальная форма полностью берет на себя дальнейшее управление программой, поэтому оператор, следующий за вызовом ShowModal, получит управление только после её закрытия. Для удаления формы с экрана используются методы Hide (спрятать) и Close (закрыть). Для модальной формы определено свойство ModalResult, доступное только во время выполнения приложения. Основные свойства формы: Active Boolean возвращает true,если форма активна; BorderIcons Определяет кнопки в заголовке окна формы; Canvas Канва формы, позволяющая рисовать на ней изображения; ClientHeight Высота клиентской области формы в пикселях; FormStyle Стиль формы; Menu Определяет объект главного меню формы; Position Определяет размер и положение окна при запуске; WindowState Определяет состояние окна (нормальное, свернутое, развернутое). Основные методы формы: Сreate создания экземпляров форм; Show и Hide управление видимостью форм на экране; Сlose закрывает форму. Основные события формы: OnActivate приложение стало активным; OnClick пользователь щёлкнул по форме; OnClose когда окно закрывается; OnCreate окно создаётся; OnDblClick пользователь дважды щёлкнул по окну; OnDestroy окно уничтожается; OnKeyDown нажата клавиша на клавиатуре; OnMouseDown нажата кнопка мыши; OnMouseMove двигается мышка; OnMouseUp отпускается кнопка мыши; OnMouseWheel Генерируется колёсиком мыши; OnResize Генерируется, когда надо изменить размеры окна. Система Delphi при добавлении новой формы в проект автоматически создает один экземпляр класса (Form1, Form2 и т. д.), внося соответствующие изменения в файл проекта(Application.CreateForm (TForm1, Form1);) управлять процессом автоматического создания форм можно, непосредственно редактируя файл проекта или выполняя настройки в окне параметров проекта. Уничтожение формы происходит с помощью методов Release, Free или Destroy, после чего работа с этой формой становится невозможна, и любая попытка обратиться к ней или ее компонентам вызовет исключение(ошибку). Предпочтительным методом удаления формы считается метод Free, поскольку он предварительно проверяет возможность удаления. При закрытии и уничтожении формы генерируются следующие события, указанные в порядке их возникновения: OnCloseQuery (определяет, может ли быть закрыта данная форма); OnClose (используется для изменения стандартного поведения формы при закрытии); OnDeActivate (используется для освобождения ресурсов); OnHide; OnDestroy. Параметр Sender имеет тип TObject, и имеет значение объекта - источника события, в обработчике которого он используется (если на Форме несколько одинак. компонентов, выполняющих одинак. функции, то достаточно одного комплекта обработчиков, а выяснить, к какому компоненту относится событие обрабатываемое именно сейчас, позволит именно параметр Sender). Работая с параметром Sender, можно обойтись без выяснения имени компонента-источника. Конструкция (Sender as TObject) позволяет работать с источником события как с соответствующим объектом. В частности, если после (Sender as TEdit) поставить точку, то Delphi выдаст нам список свойств и методов компонента Edit.

44. Обработка исключительных ситуаций .Большинство разработчиков на Delphi создают довольно сложные программы. Сложная программа подразумевает разносторонее взаимодействие с операционной системой и приложениями операционной системы. Любое из этих взаимодействий может завершиться неправильно. Примеров этого можно привести очень много, от банального деления на ноль, до открытия несущ файла. При обработке такой ситуации Delphi, как обычно, работает с объектами. С точки зрения компилятора Delphi исключительная ситуация - это объект. Для работы с этим специфичным объектом в Delphi были введены следующие языковые конструкции: try .. except и try .. finally. Блок try..except.Итак, конструкция try .. except имеет следующий синтаксис try {исполняемый код}; except on Exceptionl do {код, исполняемый в случае возник ошибки 1}; on Exception2 do {код, исполняемый в случае возникновения ошибки 2}; else {код, обработчик всех не перехваченных ранее ошибок}; end;Если при выполнении кода, размещенного в разделе try, генерируется исключение, то выполнение этого раздела прекращается и управление передается коду, размещенному в разделе except. Раздел except может использоваться двумя способами. Во-первых, в нем могут располагаться любые операторы, кроме обработчиков исключений, начинающихся с приставки on. Это и операторы сообщения об ошибке, и команды, позволяющие освобождать системные ресурсы, и др. Во-вторых, раздел except используется для обработки исключений. В этом случае в него могут включаться только операторы обработки исключений. Если среди обработчиков встретился обработчик, соответствующий сгенерированному исключению, то выполняется оператор этого обработчика, исключение разрушается и управление передается коду, расположенному после оператора on Exception do. Раздел, расположенный после ключевого слова else, служит для обработки любых исключений, не описанных в разделе except. Этот раздел не является обязательным. Если при обработке исключительной ситуации не будет найден подходящий обработчик, то произойдет обработка системным обработчиком исключений.

Блок try...finallyСмысл этой конструкции можно описать одним предложением: операторы, стоящие после finally, выполняются всегда. Следующая конструкция try .. finally служит для защиты кода, записанного в разделе finally от исключительных ситуаций, которые в силу каких-либо причин могут происходить в разделе try.

try {операторы, способные создать исключительную ситуацию};finally {защищенные операторы, выполняемые в любом случае};end; Итак, операторы, которые размещены после ключевого слова finally, будут выполняться в любом случае, была сгенерирована исключительная ситуация или нет. Если в разделе try была сгенерирована исключительная ситуация, то управление немедленно передается разделу finally. Также, если исключительной ситуации в разделе, try не было, блок finally будет выполняться. Даже если в разделе finally произойдет ошибка, выполнение операторов этого раздела будет продолжено до конца. Блок try...finally, как можно догадаться, еще называется блоком защиты ресурсов. Важно обратить внимание на такой факт: данная конструкция ничего не делает с самим объектом — исключительной ситуацией. Задача try...finally — только прореагировать на факт нештатного поведения программы и проделать определенные действия. Сама же ИС остается.Блоки защиты ресурсов и обработчики ИС, как и другие блоки, могут быть вложенными.Например, в операционную систему Windows встроена утилита Dr. Watson, которая занимается сбором информации о необработанном исключении и ее отправкой на специальный сервер компании Microsoft