Понятие функции заданной неявно, теорема о существовании непрерывности и дифференцируемости заданной неявно

Функция y = f(x) называется функцией, заданной неявно (или неявной функцией) уравнением

F(x,y) = 0

(1)

и прямоугольником D : a ≤ x ≤ b , c ≤ y ≤ d , если

1) F(x,y) определена в D ;

2) "x О [a, b] уравнение F(x, y) = 0 имеет единственное решение y О [c, d] .

Иначе говоря, уравнение (1) определяет функцию y = y(x) ( x О [a,b] ) такую, что F(x, y(x)) ≡ 0 .

Аналогично определяют неявные функции любого числа переменных как функции, заданные уравнением и областью.

Условия существования неявной функции

Теорема Пусть

1. функция F(x, y) непрерывна в прямоугольной окрестности

D = { (x, y): |x − x0| < δ1, |y − y0| < δ2 }

точки (x0, y0) , причем F(x0, y0) = 0 ;

2. функция F(x, y) при каждом фиксированном x О (x0 − δ1, x0 + δ1) строго монотонна по y на интервале (y0 − δ2, y0 + δ2) .

Тогда существует окрестность точки x0 , в которой уравнение F(x, y) = 0 определяет функцию y = y(x) ( y(x0) = y0 ), непрерывную в этой окрестности.

Понятие обыкновенного дифференциального уравнения, порядок уравнения, решение

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x), … , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Уравнение первого порядка разрешенное относительно производной, теорема о существовании и единственности решения задачи Коши для уравнения первого порядка разрешенного относительно производной

Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка, записанное в нормальной форме:

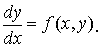
Областью определения уравнения называется область D определения правой части уравнения f(x, y), D ⊂ R² .

Функция y = y(x) является решением задачи Коши

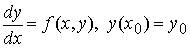
если y = y(x) дифференцируема на [a, b] , (x, y(x)) ∈ D для всех x из [a, b] , y(x₀) = y₀ , x₀∈[a, b], и при подстановке в уравнение обращает его в тождество:

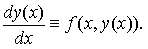
Фундаментальным результатом теории обыкновенных дифференциальных уравнений является теорема существования и единственности решения задачи Коши:

Пусть функция f(x, y) и ее частная производная f_y(x, y) непрерывны в некоторой области D плоскости x0y и точка (x₀, y₀) принадлежит области D.

Тогда :

— в некоторой окрестности (x₀ − δ, x₀ + δ) точки x₀ существует решение задачи Коши

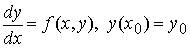
— если y = φ₁(x) и y = φ₂(x) два решения задачи Коши, то φ₁(x) = φ₂(x) на (x₀ − δ, x₀ + δ) .

Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x₀, y₀) области D проходит единственная интегральная кривая уравнения.

Бесконечное множество решений уравнения

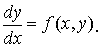
можно рассматривать как однопараметрическое семейство функций y = φ(x; x₀) — семейство решений задачи Коши

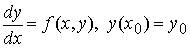
элементы которого различны для разных значений x₀ . Иными словами область D "расслаивается" на интегральные кривые y = φ(x; x₀) .

Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x₀ . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.