Тема 2, 3. Розв’язання диференціальних рівнянь, що дозволяють знизити порядок.

Одним з методів інтегрування диференціальних рівнянь другого порядку є метод пониження порядку. Суть методу полягає в тому, що за допомогою заміни змінною (підстановки) дане диференціальне рівняння зводиться до рівняння першого порядку.

Розглянемо три типи рівнянь, які допускають зниження порядку:

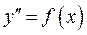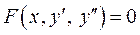а) ; б) ; в) .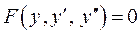

Рівняння а) розв’язано відносно похідної другого порядку і не містить шуканої функції 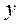та її похідної .

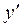Рівняння б) не містить явно шуканої функції .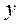

Рівняння в) не містить явно шуканої змінної .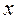

Для рівняння а) порядок можна понизити безпосередньо шляхом послідовного інтегрування рівняння. Тоді інтегруємо і одержуємо

.

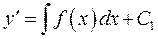Далі інтегруємо отримане рівняння відносно змінної 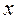і знаходимо 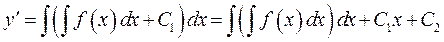– загальний розв’язок даного диференціального рівняння.

Приклад 1.Розв’язати рівняння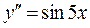

Інтегруємо послідовно два рази дане рівняння і отримаємо:

;

;

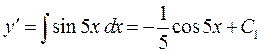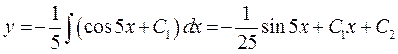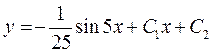– загальний розв’язок даного рівняння.

Приклад 2.Розв’язати рівняння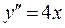

Інтегруємо послідовно два рази дане рівняння і отримаємо:

;

;

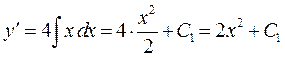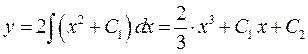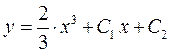– загальний розв’язок даного рівняння.

Для розв’язування рівняння б) 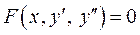треба ввести допоміжну змінну 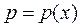, 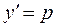. Тоді 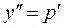і рівняння має вигляд 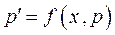, 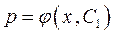. Замінимо 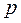на 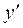і отримаємо рівняння 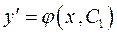. Для знаходження 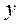достатньо про інтегрувати останню рівність.

Загальний розв’язок рівняння буде мати вигляд .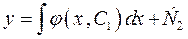

Приклад 3.Розв’язати рівняння .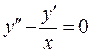

Нехай 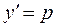, , 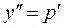тоді 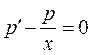це рівняння з відокремленим змінними 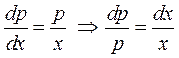. Інтегруємо його і отримаємо 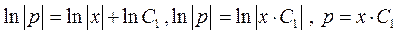. Повернемося заміни і одержимо 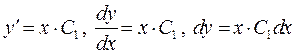, інтегруємо .

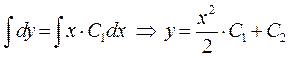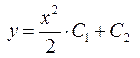– загальний розв’язок даного рівняння.

Для розв’язування рівняння в) 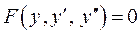треба ввести допоміжну функцію

.

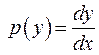Враховуючи, що 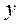залежить від 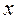і використовуючи правило диференціювання складної функції, одержимо, що

.

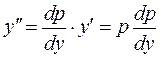Тому рівняння в) прийме вигляд 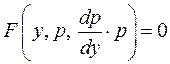, тобто буде рівнянням першого порядку відносно допоміжної функції .

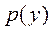Після розв’язування цього рівняння треба повернутися до шуканої функції 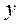шляхом підстановки замість 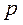її значення 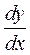і розв’язати одержане диференціальне рівняння першого порядку відносно .

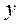Приклад 4.Знайти загальний розв’язок рівняння

.

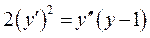Задане диференціальне рівняння не другого порядку, яке явно не містить аргументу 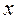. Тому використаємо допоміжну функцію.

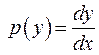та .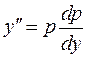

Після підстановки 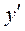та 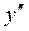в задане диференціальне рівняння одержимо диференціальне першого порядку

;

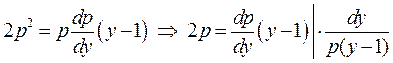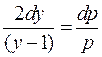– рівняння з відокремленими змінними, інтегруємо

;

.

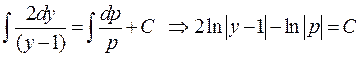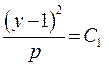Підставимо замість 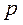її значення 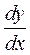і одержимо диференціальне першого порядку відносно шуканої функції .

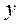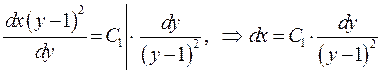, інтегруємо і маємо 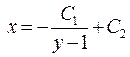; 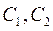– довільні сталі.

Звідси, 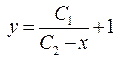– загальний розв’язок рівняння.