Кері матрица.Матрица рангісі

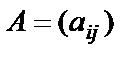
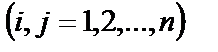квадрат матрица қарастырайық.

1.Анықтама.Анықтауышы нолге тең матрицаерекше, ал нолге тең емес матрицаерекше емес матрицадеп аталады.

Кез келген сан үшін мына теңдігін қанағаттандыратындай кері сан табылады. Квадрат матрица үшін де осындай ұғым енгіземіз.

Анықтама.А квадрат матрица үшін мына

теңдікті қанағаттандыратын матрица А матрицаныңкері матрицасыдеп аталады.

Кері матрицаны мына формуламен табады:

,

мұндағы -матрица анықтауышы, ал -берілген матрицаның элементтерінің алгебралық толықтауыштары, i=1,2,…,n; j=1,2,…,n.

Кез келген квадрат матрицаның кері матрицасы бола бермейді.

Теорема(кері матрица болуының қажетті және жеткілікті шарты). Матрицаның кері матрицасы болуы үшін ол ерекше емес ( ) матрица болуы қажетті және жеткілікті.

Мысал. матрицасының кері матрицасын табу керек.

Шешуі. Алдымен анықтауышын есептейік.

= = .

, яғни кері матрица бар. Енді элементтердің алгебралық толықтауыштарын есептейік.

, ,

, ,

, ,

, ,

.

Табылған мәндерді формулаға қойып кері матрицаны табамыз.

.

Кері матрицаның дұрыс табылғандығын теңдігін тексеру арқылы көз жеткізуге болады:

.

Берілген матрицаға кері матрицаны элементар түрлендірулер әдісімен де табуға болады. Бұл әдіс матрицаға элементар түрлендірулер қолдануға сүйенеді. Матрицаның элементар түрлендірулері деп мынадай түрлендірулерді айтамыз:

1) Матрицаны транспонерлеу;

2) Жолдардың орнын алмастыру;

3) Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейту;

4) Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейтіп басқа жолдың сәйкес элементтеріне қосу;

5) Барлық элементі ноль болатын жолды алып тастау.

Енді кері матрица табу ережесіне көшейік: Берілген матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында кері матрица пайда болады.

Мысалы, жоғарыдағы қарастырылған матрицаның кері матрицасын осы әдіспен тауып көрейік. Берілген матрицаның оң жағына бірлік матрица жазып, элементар түрлендірулер жүргіземіз.

.

Соңында бірлік матрицаның орнында пайда болған матрица кері матрица болады: .

Ерекше емес матрицалар үшін мынадай қасиеттер дұрыс болады:

1) , 2) ,

3) , 4) .

МАТРИЦА РАНГІСІ

mxn өлшемді А матрицаның бірнеше жатық және тік жолдарын сызып тастап k өлшеміді, k min(m,n), квадрат матрица алуға болады. Осы квадрат матрица анықтауышы берілген матрицаның k өлшемді минорыдеп аталады. матрицаның k-өлшемді минорлар саны болады.

Анықтама.Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады:

r=r(A)= rangA .

Анықтамадан бірден мынадай тұжырымдар жасауға болады:

1. матрицасының рангісі оның өлшемдерінің кішісінен артпайды:

r(A) min(m,n).

2. Барлық элементтері ноль болғанда ғана (нолдік матрица) матрица рангісі ноль болады.

3. n–ретті квадрат матрица ерекше емес болғанда матрица рангісі n–ге тең болады.

Мысал. матрицаның рангісін есептейік.

Шешуі. Матрица өлшемі 3х4 болғандықтан, оның рангісі 3-тен артпайды, r(A) min(3,4). Егер үшінші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі 3-ке тең болады. Үшінші ретті минорлар матрицаның бір тік жолын сызып тастағанда пайда болады:

, , , .

Үшінші ретті минорлардың бәрі нолге тең болғандықтан, ранг 3-ке тең бола алмайды. Енді екінші ретті минорлардың ішінен (олардың саны ) ең болмағанда бір нолге тең емес минор тапсақ, матрица рангісі 2-ге тең болады. Екінші ретті минорлар матрицаның бір жатық, екі тік жолын сызып тастағанда пайда болады. Айталық бірінші жатық жол мен бірінші және екінші тік жолдарды сызып тастағанда пайда болатын мына минор: , сондықтан r(A)=2.

Матрица өлшемі артқан сайын оның рангісін барлық нолден өзге минорларды есептеу жолымен анықтау қиындайды. Матрица рангісін элементар түрлендірулер әдісімен табу ондай қиындықтардан құтқарады.