Преобразование лапласа и их связь спреобразованием фурье
Необходимость выполнения условия абсолютной интегрируемости ограничивает класс функций (колебаний), к которым применимы интегральные преобразования Фурье. Так, например, широко используемый в теории электрических, цепей идеальный "скачок" напряжения (тока)
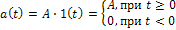
не удовлетворяет условию абсолютной интегрируемости, его энергия бесконечно велика, и потому спектральная функция не определена. Действительно, используя (23) получаем
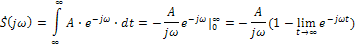
но такого предела не существует.
Для расширения класса колебаний можно модифицировать интегральные преобразования следующим образом. Пусть при 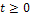 задано колебание, которое описывается функцией
задано колебание, которое описывается функцией 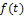 , возрастающей при увеличении
, возрастающей при увеличении 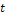 не быстрее экспоненты
не быстрее экспоненты 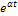 . Иначе говоря, функция
. Иначе говоря, функция 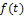 имеет ограниченный рост. Введем убывающий (
имеет ограниченный рост. Введем убывающий ( 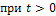 ) множитель
) множитель 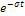 , причем положительную константу
, причем положительную константу 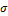 выберем так, чтобы новая функция
выберем так, чтобы новая функция
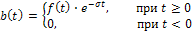
удовлетворяла условию абсолютной интегрируемости, т.е. 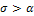 . Тогда для
. Тогда для 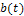 существует прямое преобразование Фурье
существует прямое преобразование Фурье
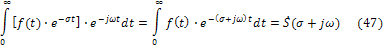
и обратное ( 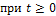 )
)
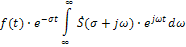
Умножив обе части последнего равенства на 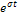 и заменив переменную интегрирования
и заменив переменную интегрирования 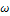 на комплексную переменную
на комплексную переменную 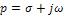 , а также
, а также 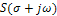 на
на 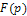 , получим
, получим
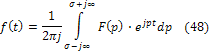
и, кроме того, (47) примет вид:
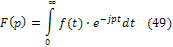
Функцию 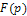 комплексной переменной
комплексной переменной  называют, изображением оригинала
называют, изображением оригинала 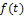 и символически это записывают так:
и символически это записывают так: 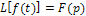 .
.
Формулы (48) и (49) называют парой преобразований Лапласа, причем формула (49) позволяет осуществить прямое преобразование и найти изображение 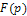 по заданному оригиналу
по заданному оригиналу 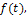 а формула (48) –обратное преобразование. Преобразования Лапласа обобщают интегральные преобразования Фурье, являющиеся их частным случаем при
а формула (48) –обратное преобразование. Преобразования Лапласа обобщают интегральные преобразования Фурье, являющиеся их частным случаем при 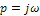 (или при
(или при 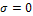 ). Поэтому преобразования Лапласа и Фурье имеют сходные свойства.
). Поэтому преобразования Лапласа и Фурье имеют сходные свойства.
Преобразования Лапласа широко используются в теории электрических цепей. Они лежат в основе операторного метода анализа, который, как и спектральный, относится к группе "частотных" методов.
ЗАДАЧИ
В зависимости от содержания всё задачи разделены на четыре группы. Поэтому каждая задача имеет номер из двух цифр: первая означает номер группы, вторая – порядковый номер задачи в группе. Типовые задачи первых трех групп разобраны в теоретической части настоящих методических указаний в примерах под номерами, совпадающими с номерами групп. В ряде случаев под одним номером объединены несколько задач с одинаковым заданием.
Четвертую группу составляют задачи комбинированных типов.
1.1. Одно из периодических колебаний, представленных на рис.7, разложить в ряд Фурье. Построить график колебания как сумму первых шести составляющих ряда (с учетом постоянной составляющей). Рассчитать действующее значение колебания, используя формулу (43).
1.2. Найти и построить амплитудные и фазовые спектры одной, из периодических последовательностей импульсов (рис.7, а-н) при следующих значениях периода и длительностей импульсов:
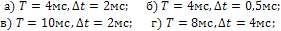
Сравнить спектры, сделать выводы.
2.1. Найти спектральную плотность одного из импульсов, изображенных на рис.8. Построить амплитудные и фазовые спектральные характеристики. Определить ширину спектра импульса. Построить спектр периодической последовательности импульсов при 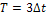 и
и 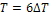 .
.
2.2. Рассчитать и построить амплитудный и фазовый спектры периодических последовательностей импульсов (рис.7.), используя понятие спектральной плотности одиночного импульса, теоремы сложения и запаздывания.
2.3. Найти спектральную плотность пакета из десяти прямоугольных импульсов длительностью 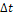 , равноотстоящих друг от друга на
, равноотстоящих друг от друга на 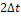 . Построить амплитудную спектральную характеристику, сравнить ее с характеристикой одиночного прямоугольного импульса и спектром периодической последовательности, полученной в результате беспредельного увеличения количества импульсов в пачке. Оценить, как будет меняться во времени спектральная характеристика, если с течением времени количество импульсов в пачке постепенно увеличивать.
. Построить амплитудную спектральную характеристику, сравнить ее с характеристикой одиночного прямоугольного импульса и спектром периодической последовательности, полученной в результате беспредельного увеличения количества импульсов в пачке. Оценить, как будет меняться во времени спектральная характеристика, если с течением времени количество импульсов в пачке постепенно увеличивать.
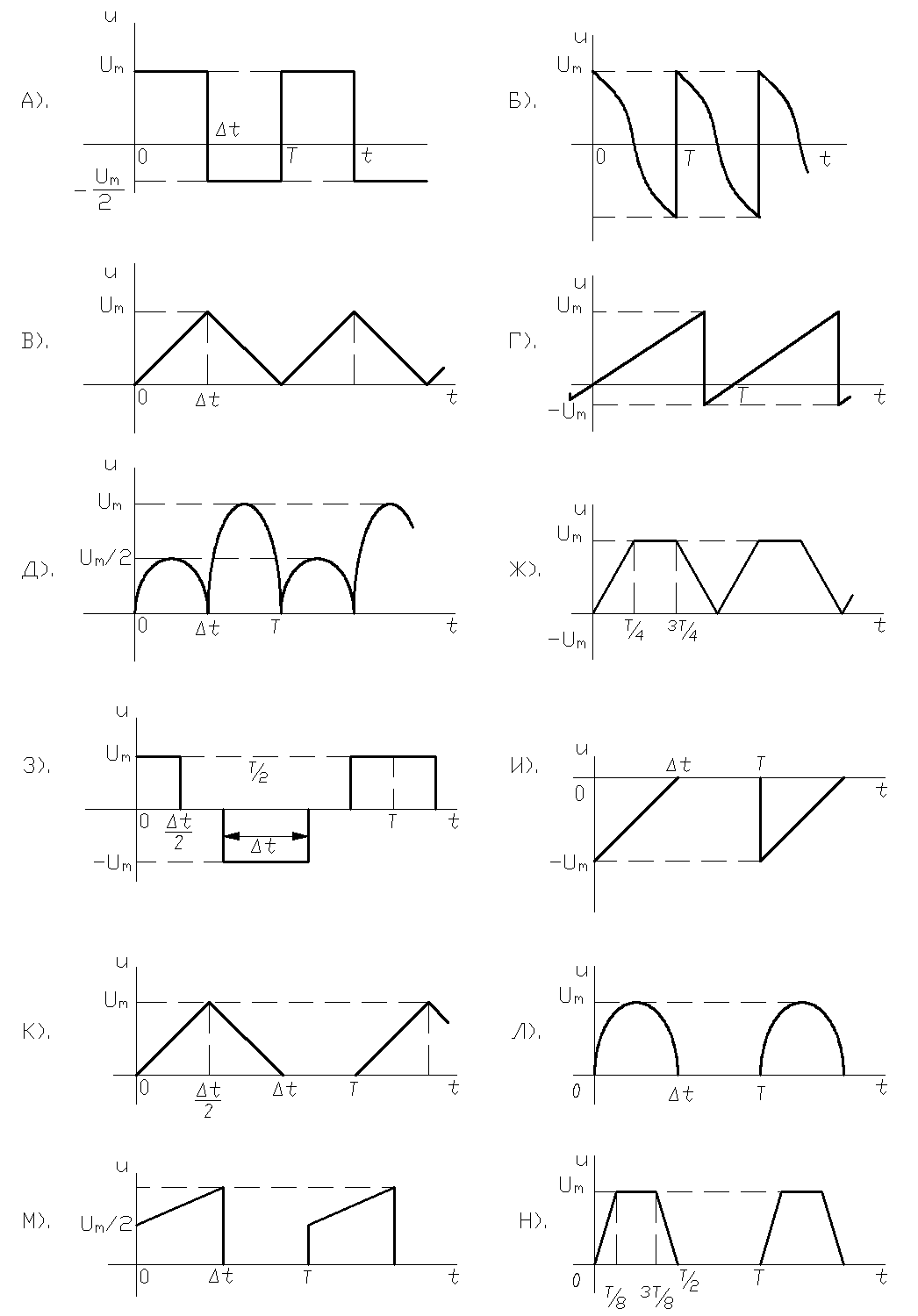 Рис.7 Рис.7 |
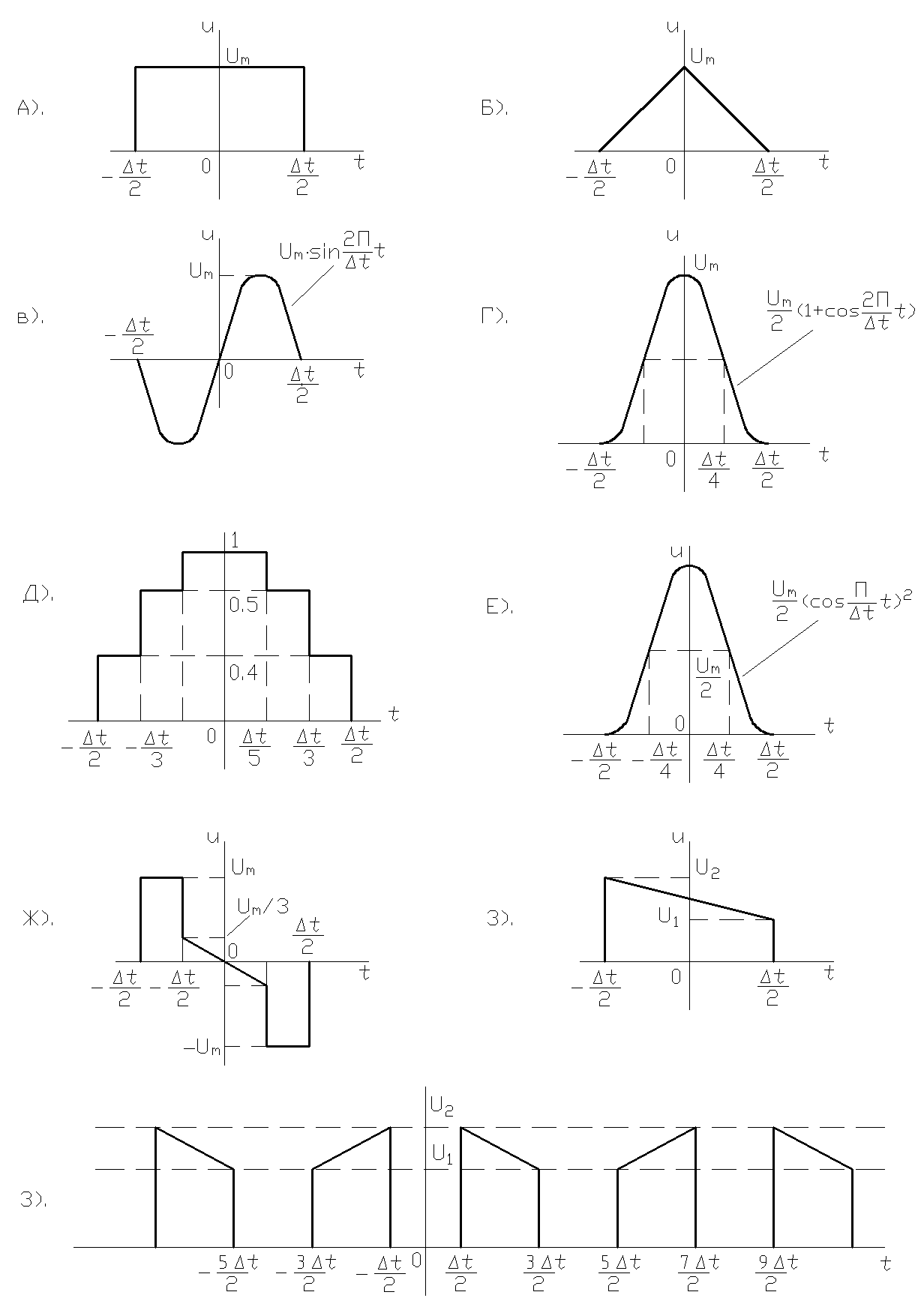 Рис.8 Рис.8 |
2.4.Дана спектральная плотность 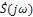 импульса, приведенного на рис.8.з. Найти ряд Фурье периодического напряжения, сформированного их таких импульсов так, как показано на рис.8.и.
импульса, приведенного на рис.8.з. Найти ряд Фурье периодического напряжения, сформированного их таких импульсов так, как показано на рис.8.и.
2.5.Рассчитать спектральную плотность напряжения, заданного выражением 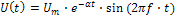
Построить амплитудную спектральную характеристику при следующих значениях параметров: 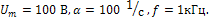
2.6. Полагая равными длительности импульсов, вычислить спектральные плотности для следующих импульсов:
-прямоугольного и треугольного (рис.8.а; рис.8.б);
-треугольного и синусоидального (рис.8.б;рис.8.в);
-синусоидального и косинусоидального (рис.8.в; рис.8.г);
-косинусоидального и квадратичного косинусоидального(рис. 8.г; рис.8.е).
Определить ширину спектра каждого импульса. Построить амплитудные спектральные характеристики, сравнить скорости убывания модуля спектральной плотности с ростом частоты. Сделать вывода.
2.7. Пирамидальный импульс (рис.8.д) представить в виде суммы прямоугольных импульсов. Используя теоремы о свойствах интегральных преобразований Фурье, рассчитать спектральную плотность заданного импульса, построить амплитудную спектральную характеристику, сравнить с характеристикой одиночного прямоугольного импульса. Сделать выводы.
2.8. Импульс, показанный на рис.8.ж, разложить на более простые составляющие. Найти спектральные плотности составляющих, а затем спектральную плотность заданного импульса, используя теоремы о свойствах преобразований Фурье. Построить амплитудные спектральные характеристики составляющих импульсов и заданного но данном рисунке.
2.9.Анализируя симметрию импульсов, представленных на рис.8, дать качественную оценку различий их спектральных плотностей. Найти спектральные плотности двух импульсов с разными видами симметрии, выделить действительную и мнимую части, построить их, сравнить, сделать выводы.
2.10. Колебание 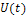 имеет спектральную плотность, модуль
имеет спектральную плотность, модуль 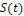 и аргумент
и аргумент  которого приведены на рис.9. Найти
которого приведены на рис.9. Найти 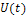 и построить график его.
и построить график его.
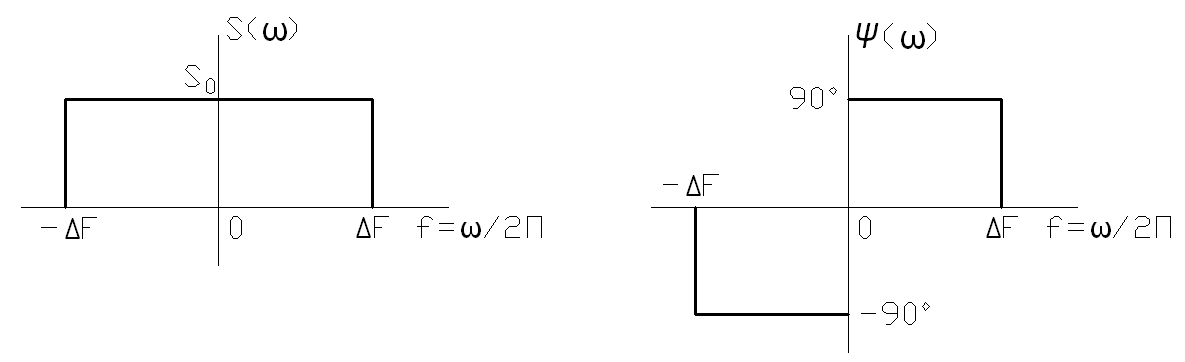 Рис.9 Рис.9 |
2.11. На рис.10 изображены действительные составляющие спектральных плотностей двух колебаний 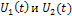 .Определить эти колебания и построить их графики при
.Определить эти колебания и построить их графики при 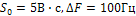
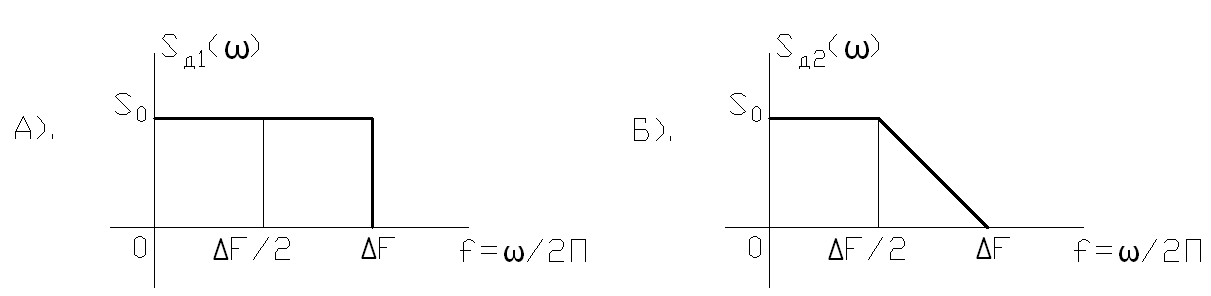 Рис.10 Рис.10 |
2.12. На рис.11 изображены мнимые составляющие спектральных плотностей двух колебаний 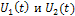 .Определить эти колебания для
.Определить эти колебания для 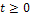 и построить их графики.
и построить их графики.
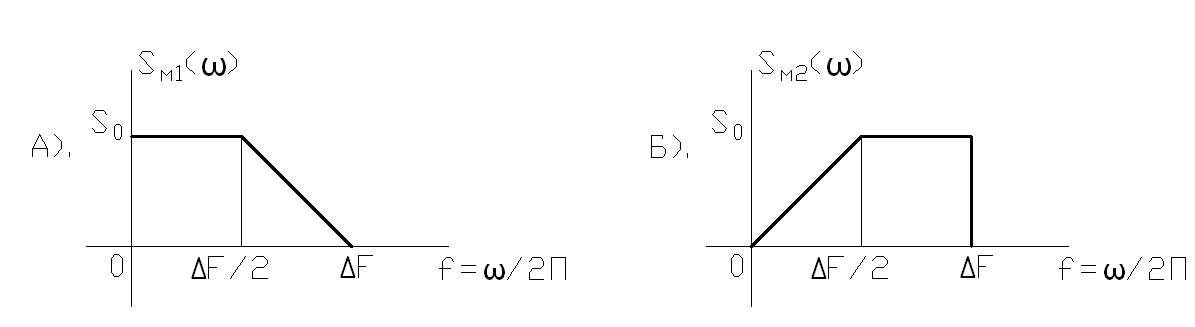 Рис.11 Рис.11 |
2.13.Для напряжения 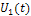 известна мнимая составляющая спектральной плотности
известна мнимая составляющая спектральной плотности 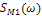 , а для напряжения
, а для напряжения 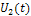 действительная составляющая
действительная составляющая 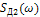 , приведенные на рис.11.а ирис.11.б соответственно. Определить эти напряжения при
, приведенные на рис.11.а ирис.11.б соответственно. Определить эти напряжения при 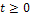 ,построить графики, сравнить. Сделать вывода.
,построить графики, сравнить. Сделать вывода.
3.1. Найти комплексный коэффициент передачи 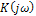 одного из четырехполюсников, изображенных на рис.12. Выразить в общем виде и построить, как функции частоты
одного из четырехполюсников, изображенных на рис.12. Выразить в общем виде и построить, как функции частоты 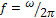 , амплитудно-частотную и фазо-частотную характеристики четырехполюсника при следующих значениях параметров элементов:
, амплитудно-частотную и фазо-частотную характеристики четырехполюсника при следующих значениях параметров элементов:
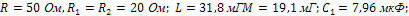
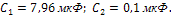
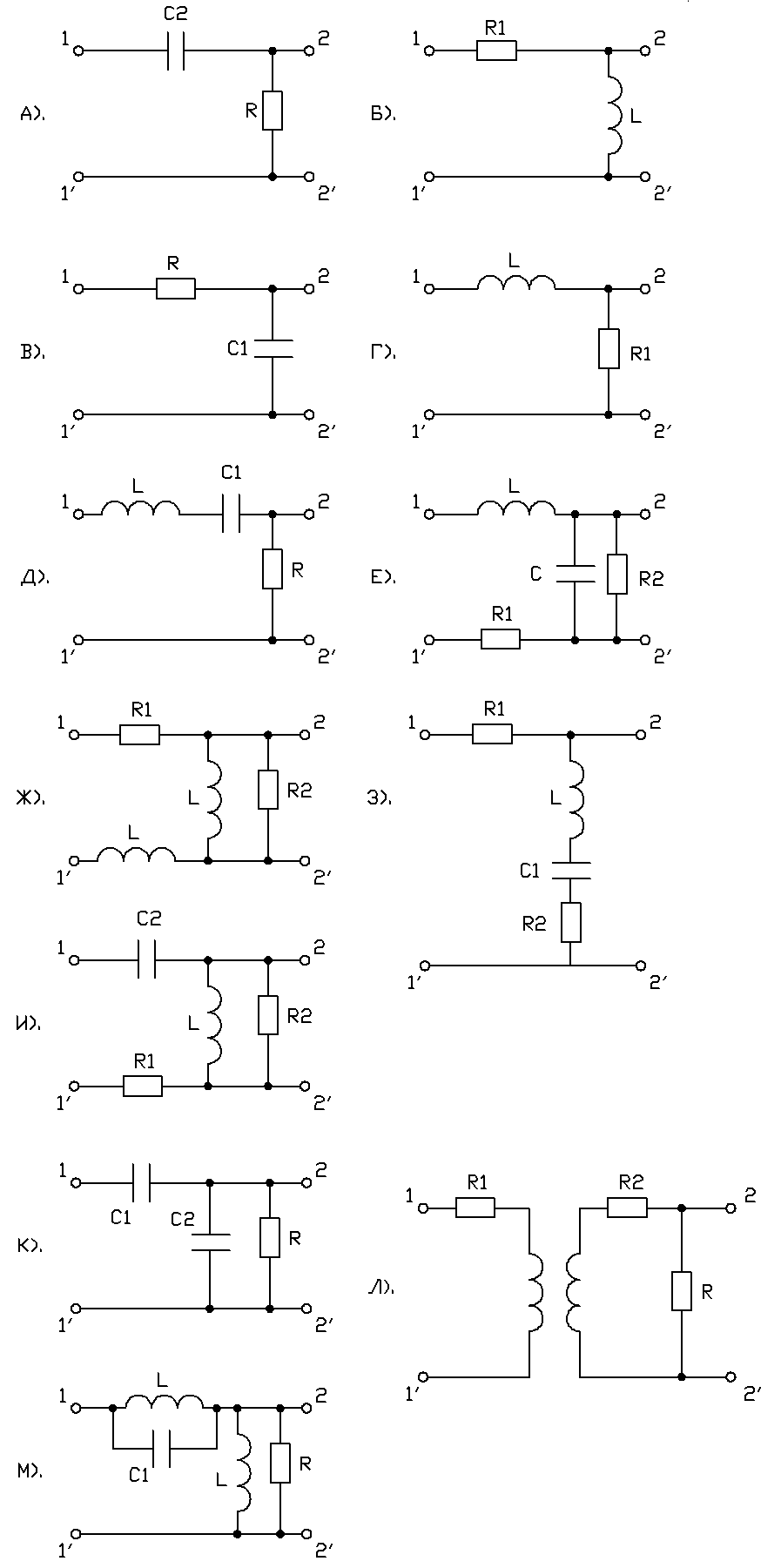 Рис.12 Рис.12 |
3.2. На вход одной из цепей, приведенных на рис.12, подается одиночный импульс напряжения из показанных на рис.8. Определить и построить напряжение на выходе цепи при 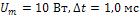 и параметрах цепи из задачи 3.1.
и параметрах цепи из задачи 3.1.
3.3. Периодическое напряжение (рис.7) подается на вход линейной цепи (рис.12) , где r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 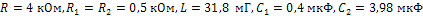
Найти напряжение на выходе цепи, если 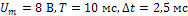 построить график выходного напряжения, суммируя первые четыре слагаемые ряда Фурье.
построить график выходного напряжения, суммируя первые четыре слагаемые ряда Фурье.
3.4. Даны входной и выходной сигналы линейной цепи (рис.13) причем 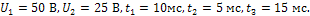 Определить комплексный коэффициент передачи цепи l Unicode MS" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/></w:rPr><m:t>K(jП‰)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
Определить комплексный коэффициент передачи цепи l Unicode MS" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/></w:rPr><m:t>K(jП‰)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 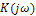 , построить характеристики:
, построить характеристики: 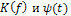
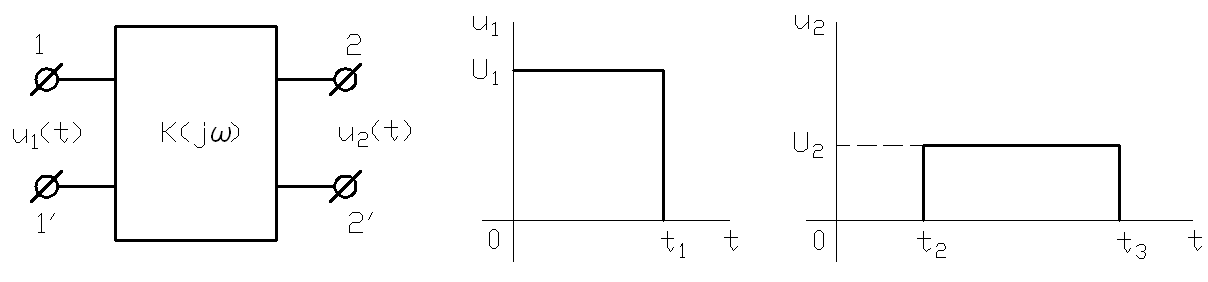 Рис.13 Рис.13 |
3.5. Цепь, показанная на рис.14, где 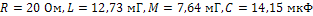 , подвергается совместному воздействии источников э.д.с.
, подвергается совместному воздействии источников э.д.с. 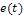 и тока
и тока 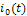 . Определить и построить выходное напряжение
. Определить и построить выходное напряжение 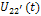 для случаев, когда:
для случаев, когда:
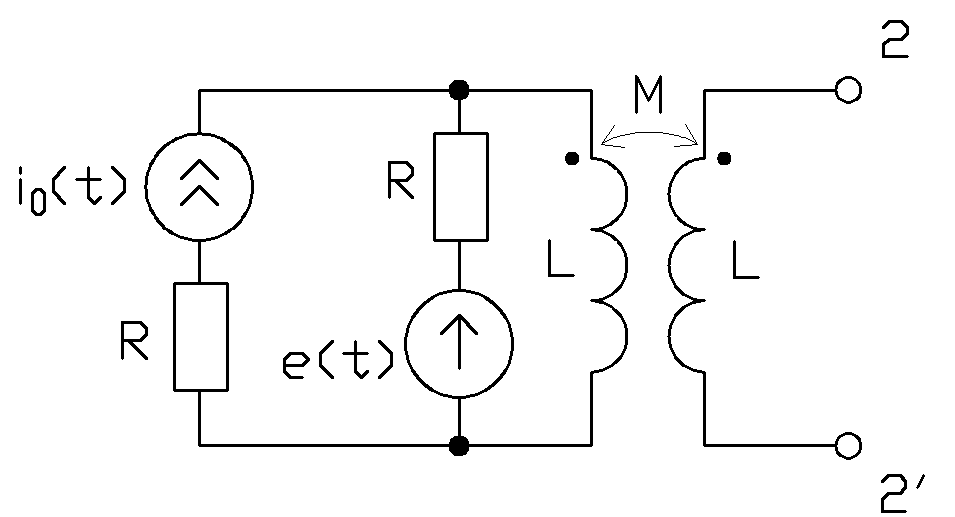 Рис.14 Рис.14 |
а). 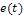 представляет собой периодическое колебание (рис.7), а
представляет собой периодическое колебание (рис.7), а 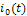 - импульс тока (рис.8при замене
- импульс тока (рис.8при замене 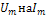 );.
);.
б). 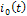 представляет собой периодический ток (рис.7), а
представляет собой периодический ток (рис.7), а 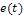 - импульс напряжения (рис.8). Считать что
- импульс напряжения (рис.8). Считать что 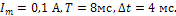 параметры воздействий имеют значения
параметры воздействий имеют значения 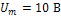 .
.
4.1. На вход последовательной (или параллельной) 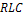 - цепи (рис.15), в которой
- цепи (рис.15), в которой 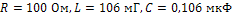 , подается периодическое напряжение (рис.7) с параметрами:
, подается периодическое напряжение (рис.7) с параметрами: 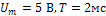 ,
, 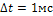 .
.
Определить показания приборов электромагнитной системы (все амперметры и
вольтметры 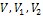 ) и магнитоэлектрической системы (вольтметр
) и магнитоэлектрической системы (вольтметр 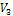 ). Учитывать не менее шести составляющих рядя Фурье.
). Учитывать не менее шести составляющих рядя Фурье.
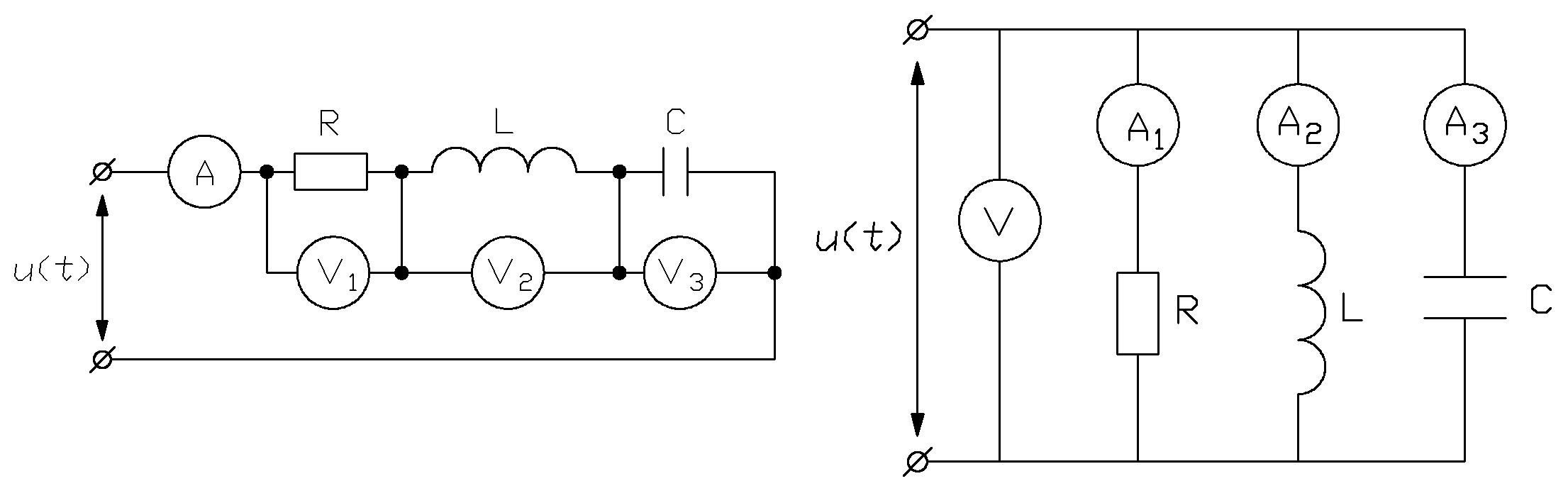 Рис.15 Рис.15 |
4.2. Определить показания приборов электромагнитной системы в цепи (рис 16, где 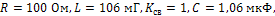
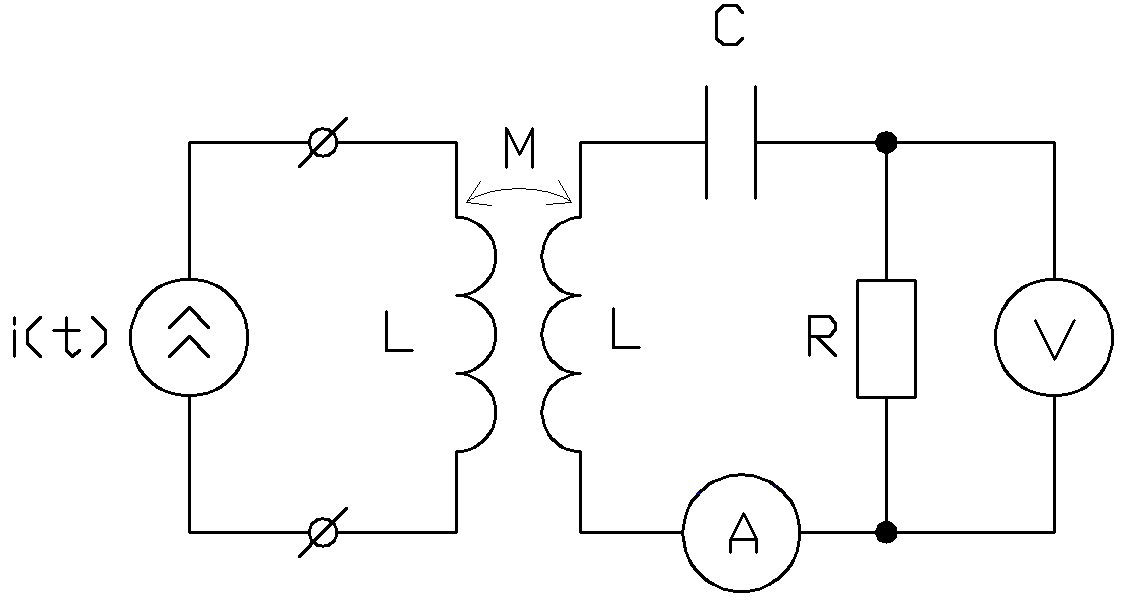 Рис.16 Рис.16 |
при воздействии источника тока
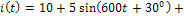
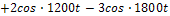
Решить задачу для случая, когда
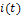 - периодический ток более сложной формы (рис.7) с параметрами:
- периодический ток более сложной формы (рис.7) с параметрами:
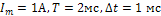
4.3. На цепь (рис.17), где 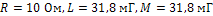 т. е.
т. е. 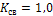 , поданы два периодических напряжения из показанных на рис.7:
, поданы два периодических напряжения из показанных на рис.7: 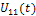 с периодом
с периодом 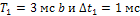 и
и 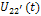
с периодом 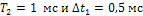
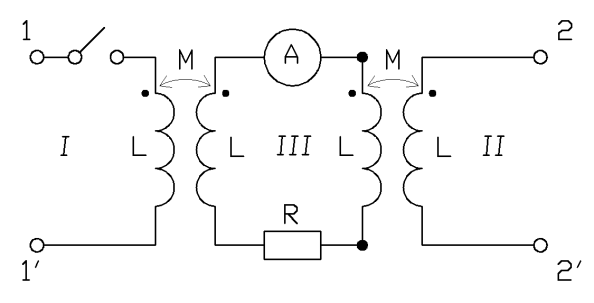 Рис.17 Рис.17 |
Полагая источники напряжения идеальными, определить показания амперметра электромагнитной системы, включенного в контур III, в случаях, когда:
а) ключ в контуре I замкнут;
б) ключ разомкнут.
Учитывать не менее шести составляющих ряда Фурье.
Литература
- Теоретические основы электротехники / К.С.Демирчан и др. – СПб.: Питер, 2006.
- Теория линейных электрических цепей в упражнениях и задачах / М.Р. Шебес.- М.: Высшая школа, 1989.
- Спектры и анализ / А.А. Харкевич.
