Переходные характеристики.

Переходная, или временная, характеристика (функция) звена представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным. Сказанное иллюстрируется на рис.2.6,а и б. На рис. 2.6,б показаны три различных вида переходных характеристик, соответствующих различным типам звеньев, которые мы рассмотрим далее.

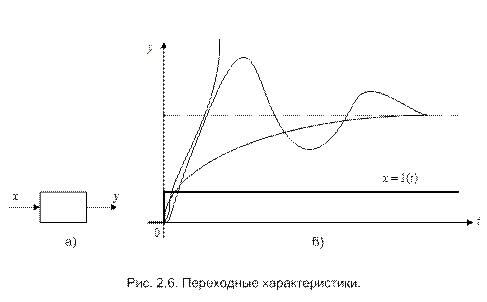
Таким образом, h(t) – это выражение для y(t) при x(t) = 1(t).

Наряду с переходной характеристикой применяется импульсная переходная (временная)характеристика или функция, называемая еще весовой функцией (функцией веса). Эта характеристика представляет собой реакцию звена на единичный импульс. Единичный импульс (единичная импульсная функция, или дельта-функция) – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности. На рис.2.4,б он условно показан в виде утолщения на оси ординат. На рис. 2.7 изображены типичные формы самих импульсных переходных характеристик.

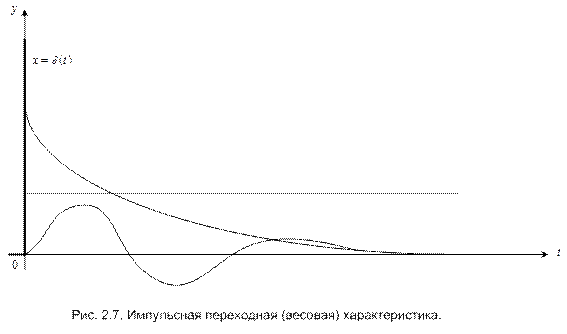
Импульсная переходная характеристика обозначается w(t); единичный импульс обозначается δ(t). Таким образом, w(t) – это y(t) при x(t) = δ(t).

При этом, согласно определению,

.

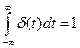Дельта-функция просто связана с единичной ступенчатой функцией:

.

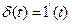Из этого выражения следует аналогичная связь между переходной и весовой функциями линейных звеньев:

w(t) = h’(t)

и наоборот

.

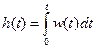Учитывая это простое соотношение между переходной и весовой функциями, ниже будем применять главным образом первую из них, имея в виду, что вторую при необходимости всегда можно получить дифференцированием по формуле w(t) = h’(t).

Зная переходную или весовую функцию, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:

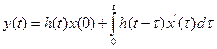, (2.8)

где х(0) – значение х(t) при t = 0;

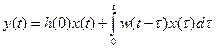. (2.9)

Эти формулы легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки.

Переходные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразования Лапласа над уравнением звена, записанным в общем виде согласно уравнению (2.3,а):

.

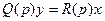Считая начальные условия нулевыми и учитывая, что обе части этого уравнения представляют собой сумму производных с постоянными коэффициентами, получим:

.

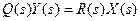Здесь 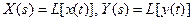- изображения Лапласа функций x(t) и y(t); Q(s) и R(s) – полиномы, отличающиеся от исходных полиномов Q(p) и R(p) только заменой оператора дифференцирования р на комплексную переменную s = c + jω. Отсюда

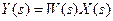, (2.10)

где 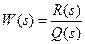- передаточная функция звена (с заменой р на s).

В случае, когда входное воздействие x(t) представляет собой единичный импульс δ(t), учитывая, что его изображение по Лапласу 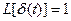, из (2.10) получаем следующее выражение для изображения весовой функции звена:

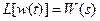, (2.11)

т.е.

.

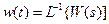Таким образом, весовая функция определяется через передаточную функцию по формуле обратного преобразования Лапласа, т.е. является ее оригиналом.

В случае, когда x(t) = 1(t), учитывая, что L[1(t)] = 1/s, из (2.10) получаем выражение для изображения переходной характеристики:

.

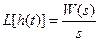Соответственно переходная характеристика звена

.

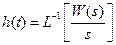Выражения (2.10) и (2.11) можно трактовать как определения передаточной функции. Согласно (2.10), передаточная функция определяется как отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях. Согласно (2.11), передаточная функция есть изображение Лапласа весовой функции.

Основные параметры переходной функции:

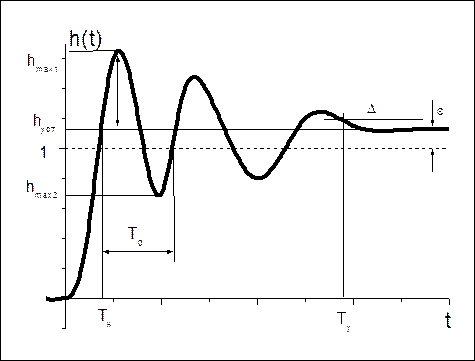
Рис. 2.8. Переходная характеристика САУ.

§ статическое отклонение (статическая ошибка) ε = 1(t) – h_уст. Она характеризует разность между входным и выходным сигналами в установившемся режиме. Системы, у которых статическое отклонение не равно нулю (ε <> 0) называются статическими. Системы, у которых ε = 0, называются астатическими.

§ Динамическое отклонение, т.е. разность между максимальным отклонением и установившемся значением h_max – h_уст.

§ Время регулирования (управления) T_у – это время переходного процесса. Это время, после которого разность между текущим значение выходного сигнала и установившимся значением будет иметь малую величину Δ. Как правило, Δ принимают равным 5% от h_уст.

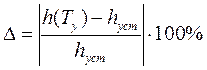
Время регулирования характеризует быстродействие системы автоматического управления. Чем меньше T_у, тем выше быстродействие.

§ Перерегулирование σ, %. Определяется выражением:

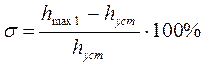
(В реальных системах перерегулирование обычно составляет 10 – 30%).

§ Частота колебаний процесса ω = 2π/T₀, где T₀ – период колебаний.

§ Время нарастания (установления) T_н – время, за которое система достигает установившегося значения.

8.Логарифмические частотные характеристики САУ.

§ Логарифмический декремент затухания, определяется по формуле:

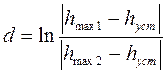
§ Число колебаний n – число максимумов h(t) на промежутке от 0 до T_у.

Функции 1(t) и δ(t) можно использовать для экспериментального определения передаточной функции элемента системы управления:

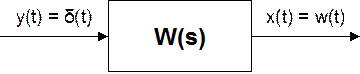
Первый подход: подадим на вход d^*(t). Пусть d*(t) ≈ d(t) (т.к. d(t) физически не реализуема), измерим w^*(t) ≈ w(t). Теперь можно вычислить L[w^*(t)] = W^*(s) ≈ W(s).

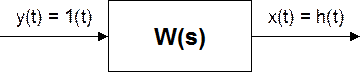
Второй подход: На вход подаем 1(t). Измеряем h(t) и вычисляем передаточную функцию. W(s) = L[d/dt(h(t)].