Формулы преобразование координат точек пространства

ГЛАВА 6

МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ.

СМЕШАННОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

КООРДИНАТЫ ТОЧЕК В ПРОСТРАНСТВЕ. РЕШЕНИЕ ПРОСТЕЙШИХ ЗАДАЧ В КООРДИНАТАХ

Системой координат в пространстве называется объединение точки О и базиса {е₁, е₂ е₃} трехмерного векторного пространства Vз. Система координат обозначается так: (О,е₁,е₂ , е₃).

Если дана система координат (О,е₁,е₂ , е₃),то координатами точки М в этой системе координат называются координаты её радиус вектора ОМ в базисе{е₁,е₂, е₃},т.е. если ОМ= хе₁+ уе₂ +z е₃ , то числа х, у и z – координаты точки М , М(х,у, z ).

Если дана система координат (О,е₁,е₂е₃ ) и А(х₁,у₁, z₁ ),

В(х₂ ,у₂, z₂ ) то вектор АВ имеет координаты АВ(х₂ – х₁, у₂ – у₁,, z₂ – z₁ ).

Если дана прямоугольная декартова система координат

(О,i, j, k) и А(х₁,у₁, z₁ ), В(х₂ ,у₂, z₂ )

___________________. .

то │АВ│= √ (х₂ – х₁)² + (у₂ – у₁)² + (z₂ – z₁)²

Если дана система координат и А(х₁,у₁, z₁ ), В(х₂ ,у₂, z₂ ) и С(х,у,z ), а (АВ,С) = λ , то

х = (х₁ + λ х₂) :(1 + λ), у = (у₁ + λ у₂):(1 + λ), z = (z₁ + λ z₂):(1 + λ).

Эти формулы называются формулами деления отрезка в данном отношении.

ЗАМЕЧАНИЕ. Во всех задачах этого пункта, где нет специальной оговорки, предполагается, что система координат прямоугольная декартова.

6.1. АВСДА₁В₁С₁Д₁ – параллелепипед. АВ = е₁, АД = е₂, АА₁= е₃.Построить точки М(1/2, 1/2, 1/3), Р(1, -1/3, -1), К(1, 0, -5/4).

6.2. АВСДА₁В₁С₁Д₁ – куб со стороной 2.В системе координат (О, i, j, k)

i↑ ↑АД, j↑ ↑АВ, k↑ ↑АА₁ . Найти координаты точек Д₁, С₁, если О - точки пересечения диагоналей грани ВСС₁В₁.

6.3. АВСД – тетраэдр. Назовите все координатные оси и координатные плоскости аффинной системы координат а) (А, АВ,АС, АД),

б) (Д, ДВ, ДА, СД) .

6.4. Через точку А проведены прямые, параллельные осям ОХ, ОУ, ОZ аффинной системы координат, которые пересекают координатные плоскости ОУ Z, ОХ Z, ОХУ в точках А₁, А₂, А₃.

Найти координаты этих точек, если а)А(2,-3,4), б) А(-3, 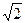, 4).

6.5. В аффинной системе координат даны точки А(3,8,-2), В(2,1,4),

С(-2,-3,6), Д(-1,4,0), Е(0,11,-6). Указать среди следующих векторов равные: АВ, ВС, ДС, СД, АД, АС, ВД, ДЕ.

ЗАДАЧА

Дан четырехугольник А(-1,0,2), В(0,2,-1), С(4,6,3), Д(3,4,6). Определить вид этого четырехугольника.

РЕШЕНИЕ

Так как специальной оговорки о системе координат нет, то данная система координат прямоугольная декартова.

1. Найдем координаты векторов АВ, ВС, СД, ДА.

АВ(1,2,-3), ВС(4,4,4), СД(-1,-2,3), ДА(-4,-4,-4). Так как АВ = ДС и векторы АВ иВС не коллинеарны, то четырехугольник АВСД – параллелограмм.

2. Выясним, является ли параллелограмм АВСД ромбом, для этого найдем длины его сторон АВ и ВС.

АВ = 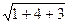= 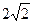, ВС = 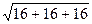= 4 .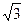

Так как длины смежных сторон АВ и ВС параллелограмма АВСД не равны, то этот параллелограмм не является ромбом.

3. Выясним, является ли параллелограмм АВСД прямоугольником, для этого найдем скалярное произведение векторов АВ и ВС.

АВ·ВС = 1· 4 + 2· 4 + (-3) · 4 = 0. Следовательно, АВ 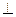ВС,значит АВСД – прямоугольник.

ОТВЕТ. АВСД – прямоугольник.

6.6. Доказать, что четырехугольник АВСД является параллелограммом, если в аффинной системе координат А(1,-3,-2), В(8,0,-4), С(4,8,-3), Д(-3,5,-1).

6.7. В аффинной системе координат найти координаты вершины Д и точки пересечения диагоналей параллелограмма АВСД, если а) А(2,5,4), В(0,1,0), С(4,1,3), б) А(2,1,1), В(3,-1,1), С(0,2,-3).

6.8. В аффинной системе координат даны координаты вершин параллелепипеда АВСДА₁В₁С₁Д₁ : А(2,-1,1), В(1,3,4), А₁(4,2,0), Д(6,0,1). Найти координаты остальных вершин.

6.9. Лежат ли точки А, В, С, заданные своими координатами в аффинной системе координат, на одной прямой: а) А(3,2,1), В(5,3,-2), С(1,1,4),

б) А(1,-3,5), В(3,-1,7), С(0,4,3), в) А(-1,0,4), В(2,3,1), С(8,9,-5),

г) А(3,0,-8), В(1,3,4), С(0,-2,1).

6.10. Найти в аффинной системе координат координаты точки, которая делит отрезок АВ в отношении λ:

а) А(2,4,-1), В(0,3,4), λ = 2, б) А(0,0,0), В(3,0,4), λ = -3,

в) А(4, 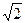, -3), В(1,5,-3), λ = ½.

6.11. Точка М – середина отрезка АВ. В аффинной системе координат найти а) координаты точки М, если А(-3,0,4), В(-3,1,2), б) координаты точки В, если М(-1,1,3), А(0,15,0).

ЗАДАЧА

В аффинной системе координат даны две вершины треугольника

А(-4,-1,2) и В(3,5,-16). Найти координаты третьей вершины С, если точка М, которая делит отрезок АС в отношении λ = 2. лежит в плоскости ОХZ, а середина отрезка ВС лежит на оси ОУ.

РЕШЕНИЕ

Обозначим координаты точки С(х,у,z).

Точка М, которая делит отрезок АС в отношении λ = 2, имеет координаты М( 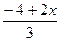, , 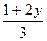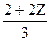) и точка М лежит в плоскости ОХZ, поэтому вторая координаты этой точке равна нулю, т.е. 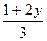=0 и значит у = ½ .

Середина Р отрезка ВС имеет координаты Р( 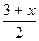, , 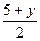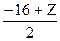) и точка Р принадлежит оси ОУ, поэтому первая и последняя ее координаты равны нулю, т.е. х = -3, z – 16.

Таким образом точка С имеет координаты С(-3, ½ , -16).

ОТВЕТ. С(-3, ½ , -16).

6.12. В аффинной системе координат даны две вершины треугольника

А(-4,-1,2) и В(3,5,-16). Найти координаты третьей вершины С, если середина АС лежит на оси ОУ, а середина ВС лежит в плоскости ОХZ.

ЗАДАЧА

В аффинной системе координат даны точки А(2,-3,6), В(1,1,1), С(5.-5,1). Выяснить, пересекаются ли прямая АВ и прямая, проходящая через точку С и начало координат.

РЕШЕНИЕ

Пусть точка Х – любая точка, лежащая на прямой АВ и делящая отрезок АВ в отношении α, тогда Х( , , ).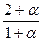

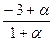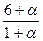Пусть У – любая точка, лежащая на прямой ОС и делящая отрезок ОС в отношении β. Тогда У( , , ).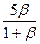

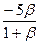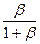Если прямые АВ и ОС пересекаются, то у них существует общая точка М, тогда М совпадает с некоторой точкой Х, лежащей на прямой АВ, и М совпадает с некоторой точкой У, лежащей на прямой ОС, следовательно,

= , = , = . (*)

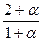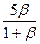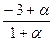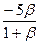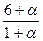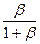Найдем α и β из системы, состоящей из первых двух из полученных уравнений (*), получим α = ½, β = ½ . Т.к. эти значения α и β не удовлетворяют третьему уравнению (*), то такой точки М не существует и , следовательно прямые АВ и ОС не пересекаются.

ОТВЕТ. Прямые АВ и ОС не пересекаются.

6.13. Дана аффинная система координат. Пересекает ли прямая, проходящая через точки А(8,-6,7) и В(-20,15,10) оси координат?

6.14. Дана аффинная система координат, А(-3,5,15), В(0,0,7), С(2,-1,4)

Д(4,-3,0). Выяснить пересекаются ли прямые АВ и СД?

6.15. В аффинной системе координат даны координаты вершин треугольника АВС: А(2,1,1), В(3,0,4) и С(0,0,16). Найти координаты середины отрезка АМ, где М – точка, которая делит отрезок ВС в отношении а) λ = 1, б) λ = 4.

6.16. Дана точка М(2,-1,1). Найти координаты точек, симметричных точке М относительно: а) начала координат, б)координатных плоскостей ОХУ, ОХZ, ОУZ, в) координатных осей ОХ, ОУ, ОZ.

6.17. Найти углы треугольника АВС, если его вершины заданы координатами: А(1,2,-4), В(4,0,-10), С(-2,6,8).

6.18. Найти расстояние а) между точками А₁(1,2,3) и А₂(1,-2,0),

В₁(2,-3,1)) и В₂(1,-3,8)), С₁(-1,-1,0) и С₂(2,3, 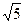), б) от начало координат до точек М(1,-3, 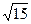) N(0,2,3), P(3, 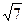, -3), Q(1,-5,6).

6.19. Найти радиус сферы с центром Мо(1,1,6), проходящей через точку

А(-2,0,2).

6.20. Доказать, что треугольник с вершинами А(3,5,-4), А(-1,1,2), С(-5,-5,-2) является равнобедренным.

6.21. Доказать, что четырехугольник с вершинами в точках А(7,2,4),

В(4,-4,2), С(6,-7,8), Д(9,-1,10) является квадратом.

6.22. Найти длины медиан треугольника, вершины которого находятся в точках А(-3,1,0), В(0,0,0), С(2,4,6).

6.23. На оси ОZ найти точку, равноудаленную от двух точек

А(-4,1,7) и В(3,5,-2).

6.24. В плоскости ОУZ найти точку, равноудаленную от точек А(3,1,2), В(4,-2,-2), С(0,5,1).

6.25. Найти координаты центра и радиус сферы, которая проходит через точки (0,0,0), (0,2,0), (1,0,0), (0,0,3).

6.26. Доказать, что четырехугольник, вершины которого находятся в точках А(7,8,9), В(9,3,7), С(5,4,3), Д(3,9,5), является ромбом.

6.27. Доказать, что треугольник является равносторонним, если: а)А(9,3,-5), В(2,10,-5), С(2,3,2), б) А(р, к, h), В(к, h, р), С(h, р, к).

ЗАДАЧА

Найти длины медианы АМ, и высоты АН треугольника АВС, если А(1,4,4), В(4,-1,3), С(-8,7,-5).

РЕШЕНИЕ

1. Найдем длину медианы АМ. Т.к. точка М является серединой отрезка ВС, то координаты точки М равны полусуммам соответствующих координат точек В и С, т.е. М(-2,3,-1 ) Следовательно, АМ = .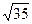

2. Найдем длину высоты АН. Пусть точка Н(х,у,z), тогда так как точка принадлежит прямой ВС, то векторы ВНи ВС коллинеарны, следовательно ВН = λВС, отсюда следует, что

х – 4 = - 12λ, у + 1 = 8λ, z - 3 = - 8λ или

х = 4 - 12λ, у = -1 + 8λ, z = 3 - 8λ,

тогда Н(4 - 12λ, -1 + 8λ, 3 - 8λ). Так как АН 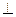ВС, то АН ВС = 0,

АН(3 - 12λ, -5 + 8λ, -1 - 8λ), ВС(-12,8,-8), поэтому из АН ВС = 0 следует:

-12(3 - 12λ) + 8( -5 + 8λ) - 8(-1 - 8λ) = 0, отсюда λ =¼ , поэтому

Н(1,1,1)

Зная координаты точек А(1,4,4) и Н(1,1,1) находим, что

АН = .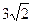

ОТВЕТ. АМ = 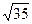, АМ = .

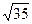6.28. Прямая АВ пересекает координатные плоскости ОХУ и ОУZ в точках М и Р. Найти длину отрезка МР, если а) А(2,1,1), В(-2,0,3), б) А(-3,1,1), В(0,-1,2).

6. 29. Найти длины медианы АМ, и высоты АН треугольника АВС, если А(1,2,-1), В(2,3,4), С(-1,-6,-5).

6.30. Найти длину биссектрисы АД треугольника АВС, если А(4,1,-2), В(2,0,0), С(-2,3,-5).

ОРИЕНТАЦИЯ ПРОСТРАНСТВА.

В векторном подпространстве Vз дан базис и три вектора

а( а₁,а₂,а₃), b(b₁,b₂,b₃), с(с₁,с₂,с₃). Векторы а,b, с компланарны тогда и только тогда, когда определитель, составленный из их координат. равен нулю, т.е.

| а₁ а₂ а₃ |

а,b, с компланарны 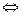| b₁ b₂ b₃| = 0.

| с₁ с₂ с₃ |

В векторном подпространстве Vз даны два базиса

I = {е₁, е₂. е₃} и II = {е₁', е₂'^, е₃'}. Известны координаты базисных векторов второго базиса в первом базисе. Определителем перехода от базиса I ={е₁, е₂. е₃} к базису II ={е₁', е₂'^, е₃'} называется определитель ∆, составленный из координат векторов е₁^’, е₂^’ е₃' в базисе{е₁, е₂. е₃}

Определитель перехода от базиса I к базису II будем обозначать так: I / II.

Пусть даны любые три базиса I, II, III пространств Vз. Определители перехода обладают следующими свойствами:

1°) I / II 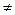0,

2°) I / I = 1,

3°) I / II = 1 : (II / I),

4°) (I / II) ( II / III) = I / III .

Обозначим Ω множество всех базисов Vз. Элементы Ω обозначим так: А= {а₁, а₂. а₃}, В = {b ₁, b ₂. b₃} и т.д.

Если в множестве Ω 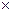Ω рассмотреть бинарное отношение

ρ 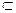Ω 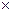Ω такое, что А ρВ 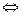А/В > 0, то из свойств определителей перехода следует, что бинарное отношение ρ является отношение эквивалентности, следовательно, множество всех базисов трехмерного векторного пространства Vз разбивается на непересекающиеся классы эквивалентности. Таких классов эквивалентности существует два и только два. Каждый из этих двух классов эквивалентности называется ориентацией векторного пространстваVз.

Векторное подпространство Vз называется ориентированным, если зафиксирована одна из его ориентацией и названа положительной, а все базисы из неё правыми, тогда вторая ориентация называется отрицательной, а все базисы из неё левыми.

Пространство называется ориентированной, если соответствующее векторное пространство ориентировано. Тогда, если базис е₁, е₂, е₃ –правые (левый) , то и система координат (О, е₁, е₂, е₃) правая (левая).

Чтобы определить будет ли данный базис правым или левым обычно рассматривают правило правой и левой руки. Пусть базис АВ, АС, АД – правый. По вектору АВ направляем большой палец правой руки, по вектору АС направляем указательный палец и, если средней палец направлен по вектору АД,то данный правый базис соответствует правой руке. Тогда, чтобы проверить будет ли базис ОХ,ОУ,ОZ правым, по вектору ОХ направляем большой палец правой руки, по вектору ОУ направляем указательный палец и, если средней палец направлен по вектору ОZ ,то базисОХ,ОУ,ОZ-правый, если же средней палец правой руки не направлен по вектору ОZ ,то базисОХ,ОУ,ОZ-левый.

Если базис АВ, АС, АД – правый, по вектору АВ направляем большой палец левой руки, по вектору АС направляем указательный палец и, если средней палец направлен по вектору АД,то данный правый базис соответствует левой руке. Тогда, чтобы проверить будет ли базис ОХ,ОУ,ОZправымдействуем как в предыдущем случае, но используем левую руку.

6.31. Выяснить, компланарны ли векторы х, у, z, если

а) х(2,-3,1), у(4,5,0), z(10,7,1); б)х(4,-3,2), у(0,1,0), z(-3,5,7);

в) х(1,3,6), у( 1/3, 1,2), z(13, 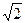,5); г) х(0,-15,1), у(3,13,-15),

z(1,5,-3).

ЗАДАЧА

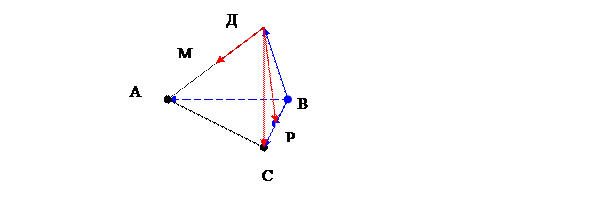
Даны точки А(1,0,3), В(0,3,-4), С(2,1,2), Д(1,-2,5). а)Доказать, что эти точки являются вершинами тетраэдра, б) точки М и Р – середины ребер АД и ВС, выяснить к какой ориентации относится базис {ДМ, ДР, ДС}, если базис{ ВА,ВС,ВД} – левый.

РЕШЕНИЕ

а) Точки А, В, С, Д являются вершинами тетраэдра тогда и только тогда, когда векторы АВ, АС, АД не компланарны. Найдем координаты этих векторов: АВ(-1,3,-7), АС(1,1,-1), АД(0,-2,2). Эти векторы не компланарны тогда и только тогда, когда определитель, составленный из их координат, не равен нулю.

| -1 3 -7 |

|1 1 -1 |= 8,

| 0 -2 2 |

следовательно, точка А, В, С, Д – вершины тетраэдра.

б) Первый способ.

Найдем координаты векторов ДМ, ДР, ДС в базисе { ВА,ВС,ВД}

ДМ(½, 0, -½),ДР(0, ½, -1),ДС(0,1,-1).

Теперь вычислим определитель, составленный из их координат.

| ½ 0 -½ |

|0 ½ -1 |= 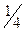>0 .

| 0 1 -1 |

Следовательно, базисы { ВА,ВС,ВД}и{ДМ, ДР, ДС} принадлежат одной ориентации, значит базис {ДМ, ДР, ДС} –левый.

Второй способ.

Базис{ ВА,ВС,ВД} соответствует правой руке. Базис

{ДМ, ДР, ДС}тоже соответствует правой руке, Следовательно, эти базисы принадлежат одной ориентации, и т.к базис { ВА,ВС,ВД} – левый, то и базис {ДМ, ДР, ДС} –левый.

ОТВЕТ Базис {ДМ, ДР, ДС} –левый.

6.32. Проверить, лежат ли точки А, В, С, Д в одной плоскости, если

а) А(3,1,1), В(-2,1,-2), С(-3,-1,0), Д(2, 0, 1,7); б) А(1,7,8), В(3,5,6),

С(-1,4,4), Д(0,7,6); в) А(1,1,0), В(-1,2,-1), С(0,-1,0), Д(-3,-3,2); г) А(1,2,2), В(0,3,3), С(2,-5,1), Д(-1,-2,2).

6.33. Изобразите куб АВСД А₁В₁С₁Д₁. Проверьте будет ли базис АВ, АД, АА₁ соответствовать правой или левой руке.

6.34. Базис АВ, АС, АД имеет правую ориентацию. Определить ориентацию базисов: а) АВ, АС, ДА; б) ДА, ДВ, ДС;

в) ВС, ВА, ВД; г)АС, СВ, СД.

6.35. Дан параллелепипед АВСД А₁В₁С₁Д₁. Базис АА₁, АВ, АД имеет левую ориентацию. Определить ориентацию базисов:

а) ДА, ДС, ДД₁; б) С₁С, С₁Д₁, С₁В₁; в) Д₁А₁, Д₁Д, Д₁В₁;

г) ВА, ВВ₁, ВС; д) РВ, РД, АР, где Р – середина ребра АД.

6. 36. В системе координат (О,е₁, е₂, е₃ ) даны точки

А₁(-7,3,-2), А₂(0,2,1), А₃(4,-1,0), А₄(-1,0,-3). Доказать, что векторы А₁А₂, А₁А₃, А₁А₄ образуют базис, и найти ориентацию этого базиса, если базис {е₁, е₂, е₃} – правый.

ФОРМУЛЫ ПРЕОБРАЗОВАНИЕ КООРДИНАТ ТОЧЕК ПРОСТРАНСТВА

В пространстве даны две системы координат I = ( О, е₁, е₂. е₃) и

II = ( О, е₁', е₂'^, е₃'), О’(х_о,у_о, z_о ) _Ι, е₁’(а₁,а ₂,, а₃)_{(е1,е2, е3)} , е₂’(b₁,b₂, b₃)_{(е1,е2 е3)},

е₃'(с₁,с ₂,,с₃) _{(е1,е2 е3)}. Если любая точка плоскости М имеет в первой системе координат координаты М(х,у, z), а во второй системе координат координаты М(х’,у’, z'), то формулы, связывающие координаты точки М в первой и во второй системах координат, имеют вид

х = а₁ х’ + b₁ у’ + с₁ z' + х_о,

у = а₂ х’ + b₂ у’ + с₂ z' + у_о (*)

z = а₃ х’ + b₃ у’ + с₃ z' + z_о

Эти формулы называются формулами преобразования координат.

Отметим, что в этих формулах столбец из коэффициентов при х’- это координаты вектора е₁’, столбец из коэффициентов при у’- это координаты вектора е₂’, столбец из коэффициентов при z' - это координаты векторае₃',а столбец из свободных членов – это координаты точки О’ в первой системе координат. Из этого следует, что определитель, составленный из коэффициентов при х’, у’, z' в формулах (*), отличен от нуля.

6.37. Написать формулы преобразования аффинной системы координат в пространстве, если даны координаты нового начала координат и новых координатных векторов в старой системе:

а) е₁'(1,0,0), е'₂(2,4,0), е'₃(-3,1, ½), О'(0,0,0);

б) е₁'(-1,1,0), е'₂(2,-1,0), е'₃(0,0, 5), О'(5,0,-2);

в) е₁'(-1,0,0), е'₂(0,1,0), е'₃(0,0, -1 ), О'(1,1,2);

г) е₁'(1,0,0), е'₂(0,1,0), е'₃(0,0, 1), О'(2,5,-1).

ЗАДАЧА

Дан параллелепипед АВСД А₁В₁С₁Д₁ и две системы координат

I =(А, АВ, АА₁,АС) и I I =(В, ВС, ВД, ВВ₁) а) Выяснить, существуют ли точки, имеющие одинаковые координаты в этих системах координат, б) зная координаты точки М (1,-2,3) в I системе координат, найти координаты этой точки во I I системе координат.

РЕШЕНИЕ

1. Составим формулы преобразования координат при переходе от системы координат I к системе координат I I. Для этого найдем координаты точки В в I системе координат и координаты векторов ВС, ВД, ВВ₁в базисе {АВ, АА₁,АС}

е1

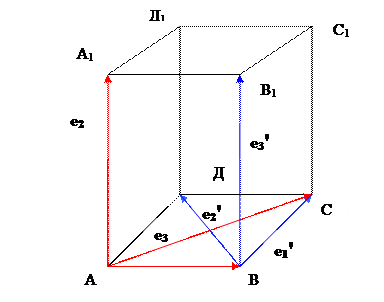
В(1,0,0), ВС(-1,0,1), ВД(-2,0,1), ВВ₁(0,1,0).

Формулы преобразования координат имеют вид:

х = -1 х' +(-2)у' +0z' +1, х = - х'-2у' +1,

у = 0 х' + 0 у' + 1z' +0, или у = z', (*)

z = 1 х' + 1 у' + 0z' +0, z=х' + у' .

2. Выясним, существует ли точка, имеющая одинаковые координаты в обеих системах координат, для этого в формулах (*) отбросим штрихи. Получим систему

х = - х-2у+1

у = z

z=х+ у

Эта система имеет единственное решение х = 0, у = ½ , z = ½ .

Следовательно, существует единственная точка, имеющая

одинаковые координаты и в I и во I I системах координат, это

точка N(0, ½ , ½ )

3. Найдем координаты точки М (1,-2,3)_l во I I системе

координат. для этого в формулы (*) подставим х = 1, у = -2,z = 3.

Получим систему

1 = - х'-2у' +1

-2 = z'

3 = х' + у'Получаем х' =6,у'= -3, z'= -2.

Следовательно, М(6, -3,-2)_{l l} .

ОТВЕТ. а) (0, ½ , ½ ), б) М(6, -3,-2)_{l l}

6.38. Диагонали куба АВСД А₁В₁С₁Д₁ пересекаются в точке О. Составить формулы преобразования координат точек при переходе от системы координат(А, АВ, АД, АА₁) к системе координат

(О, ОА, ОВ, ОС).

6.39. Дан тетраэдр ОАВС. Составить формулы преобразования координат точек при переходе от системы координат (О, ОА, ОВ, ОС) к системе координат (А, АО, АВ, АС).

6.40. Диагонали параллелепипеда АВСД А₁В₁С₁Д₁ пересекаются в точке О, а диагонали граней АДД₁А₁, АВВ₁А₁, АВСД – соответственно в точках О₁, О₂, О₃. Составить формулы преобразования координат точек при переходе от системы координат (А, АВ, АД, АА₁) к системе координат

(О, ОО₁, ОО₂, ОО₃).

6.41. Составить формулы преобразования координат точек при переходе от системы координат I = (О, е₁, е₂, е₃) к системе координат

а) (О', е₁, е₂, е₃) , где О( 3,-4,8) _I;

б) (О, е₁', е₂', е₃'), где е₁' =4е₁ +3е₂ -6е₃, е₂'= -е₁ + е₂, е₃' = - е₁ - е₂ -5е₃.

6.42. Могут ли следующие формулы служить формулы преобразования аффинных координат:

а) х = х' -3у' +z',б)х' = х+1,в) х = у',

у = х' +у',у' = у – 3, у = х',

z = х' + 1, z' = z, z = х' + у' + z' + 1,

г) х = 3х' - у' + z', д) х = х' - у' + z' + 1,

у = 4х' - у' + 3, у = - х' - у' + 2z' + 2,

z = 7х' - 2у' + z' + 4, z = z' – 3.

6.43. Дан куб АВСД А₁В₁С₁Д₁, сторона которого имеет длину а. Существует ли точка, имеющая одинаковые координаты в двух системах координат (А,i, j, k) и (С, i', j', k'), где векторы i, j, k сонаправлены соответственно с векторами АВ, АД, АА₁, а векторы i', j', k' сонаправлены соответственно с векторами С₁В₁, С₁С, С₁Д₁.

6.44. В прямоугольном параллелепипеде АВСД А₁В₁С₁Д₁ АВ = АД = а, АА₁ = b. Точка М – середина ребра СС1. В системе координат (А, i, j, k) известны координаты точки Х(-10а,12а,3а). найти координаты точки Х с системе координат (М,i', j', k'), если векторы i, j, k сонаправлены соответственно с векторами АВ, АД, АА₁, а векторы i', j', k' сонаправлены соответственно с векторами СВ, СД, СС₁.