Цепи с распределенными параметрами. Первичные параметры однородной линии. Дифференциальные уравнения однородной линии

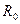-продольное активное сопротивление единицы длины линии; 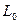-индуктивность единицы длины линии; 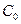-емкость единицы длины линии; 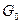-поперечная проводимость единицы длины линии. Разобьем линию на участки длиной dx, где x-расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление равно 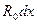, индуктивность - 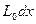, проводимость утечки - 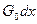и емкость - 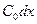. Обозначим ток в начале рассматриваемого участка линии через i и напряжение между проводами линии в начале участка u. 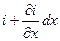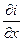Если для некоторого момента времени t ток в начале рассматриваемого участка равен i, то в результате утечки через поперечный элемент ток в конце участка для того же момента времени равен , где - скорость изменения тока в направлении x. Скорость, умноженная на расстояние dx, является приращением тока на пути dx. Аналогично, если напряжение в начале участка u, то в конце участка для того же момента времени напряжение равно 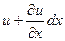. Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной dx, обойдя его по часовой стрелке:

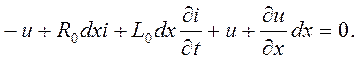
После упрощения и деления уравнения на dx получим 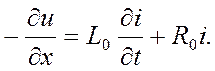(1)

По первому закону Кирхгофа, 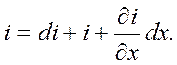(2)

Ток di (рис.2) равен сумме токов, проходящих через проводимость 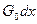и емкость :

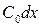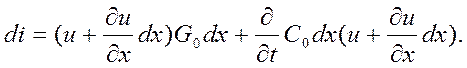
Пренебрегаем слагаемыми второго порядка малости, тогда 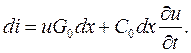(3)

Подставим (3) в (2), упростим и поделим уравнение на dx: 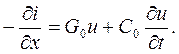(4)

Уравнения (1) и (4) являются основными дифференциальными уравнениями для линии с распределенными параметрами.

Синусоидальный режим в однородной линии. Волновое сопротивление линии. Коэффициент распространения. Общий вид уравнений однородной линии.

Обозначим комплексные действующие значения напряжения и тока на расстоянии x от начала линии через 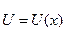и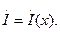

Применяя комплексную форму записи, получаем на основании уравнений 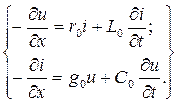(1) следующие уравнения 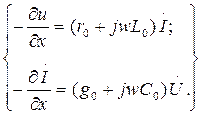(2).

Поскольку комплексные величины 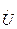и 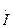не зависят от t и являются функциями только x, при переходе от уравнений (1) к (2) частные производные по x заменены обыкновенными.

Исключая из системы (2) ток 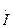, получаем уравнение относительно :

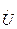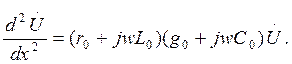(3)

Аналогично, исключая из системы (2) напряжение 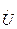, получаем уравнение относительно :

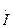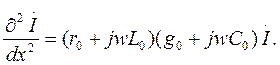(4)

Введём обозначение

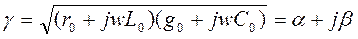(5)

и назовём эту величину коэффициентом распространения. Итак, уравнения (3) и (4) записываются в виде:

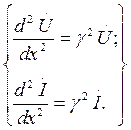(6)

Получились однородные линейные дифференциальные уравнения второго порядка. Решение первого уравнения системы (6) имеет вид:

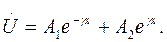(7)

Ток 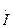проще всего находится подстановкой решения (7) в первое уравнение системы (2):

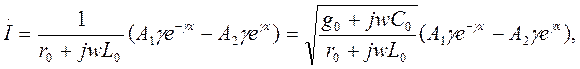
или

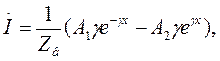(8)

где

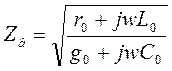(9)

называется волновым сопротивлением линии.

Подставим (5) в (7), получим:

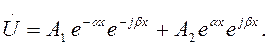
Мгновенное значение напряжения в точке x равно мнимой части выражения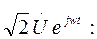

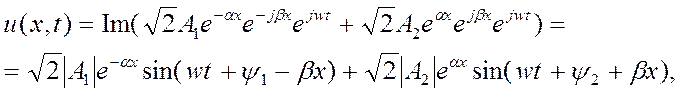(10)

где 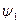, 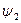- аргументы комплексных величин A1 и A2 соответственно.