Проверка адекватности модели

Лабораторная работа №5

по дисциплине «Моделирование систем»

Разработка математической модели по экспериментальным значениям натурного (вычислительного) эксперимента и оценка полученной модели на адекватность

Выполнил:

Студент гр. А-108

Литвинов И.С.

Принял:

Кирилина А.Н.

Владимир 2012

Цель занятия

Приобретение навыков обработки экспериментальных данных и получение первичной математической модели.

Общие сведения

Для того чтобы сделать выводы о результатах эксперимента, необходимо выполнить проверку значимости коэффициентов модели и проверку адекватности модели.

Проверка значимости коэффициентов

Проверка значимости коэффициента проводится независимо.

Ее можно осуществлять двумя равноценными способами: проверкой по t-критерию Стьюдента или построением доверительного интервала.

Рассмотрим второй способ.

После реализации ПФЭ необходимо рассчитать среднее значение квадрата отклонения величины от ее среднего значения - дисперсиею (воспроизводимости), которая обозначается обозначим .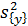

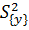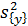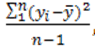= (1)

где 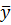– среднее арифметическое всех n результатов (параллельных опытов).

Дисперсия воспроизводимости – это средний разброс в точках относительно линии регрессии. Из формулы видно, что дисперсии всех коэффициентов равны друг другу, так как они зависят только от ошибки опыта и числа опытов.

Для случая, когда при проведении эксперимента проводилось одинаковое количество параллельных опытов, необходимо провести оценку однородности дисперсий методом Кохрена. В случае подтверждения гипотезы однородности, в дальнейших расчетах можно использовать усредненное значение дисперсий:

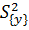
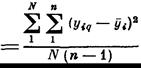
При использовании полного факторного эксперимента доверительные интервалы для всех коэффициентов равны друг другу.

Прежде всего, необходимо найти дисперсию коэффициента регрессии .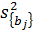

Она определяется в данном случае по формуле

,.

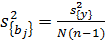Из формулы видно, что дисперсии всех коэффициентов (в том числе и эффектов взаимодействия) равны друг другу, так как они зависят только от ошибки опыта и числа опытов.

Теперь легко построить доверительный интервал (Db_j).

.

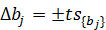Здесь t – табличное значение критерия Стьюдента при числе степеней свободы, с которыми определялась 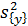(f = n - 1) (прил.1), и выбранном уровне значимости (обычно 0,05); 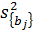- квадратичная ошибка коэффициента регрессии

Коэффициент значим, если его абсолютная величина больше доверительного интервала.

Проверка адекватности модели

После вычисления коэффициентов модели и проверки их значимости необходима проверка пригодности модели. Будем называть такую проверку проверкой адекватности модели.

Ниже приведены два рисунка с одинаковым расположением экспериментальных точек и, следовательно, одинаковым разбросом относительно линии регрессии, но с различным средним разбросом в точках (с различной дисперсией воспроизводимости S_{y}). Разброс в точках показан, как это иногда делается, отрезками прямых, составляющих доверительный интервал, равный ±2S_{y}. Модель можно считать адекватной только в первом случае.

В данном случае, разброс в точках такого же порядка, что и разброс относительно линии. Поэтому можно предполагать, что построенная модель пригодна. (Дальше выясним, как проверить это количественно.) Во втором случае опыты «слишком» точны. Требуется более сложная модель, чтобы точность ее предсказания была сравнима с точностью эксперимента (см. рис. 1).

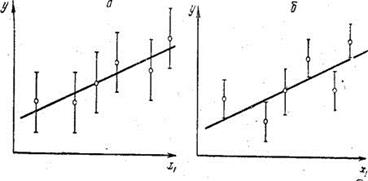
Рис. 1. Проверка адекватности модели

Это качественные соображения, а нужна количественная мера.

Для характеристики среднего разброса относительно линии регрессии вполне подходит остаточная сумма квадратов. Неудобство состоит в том, что она зависит от числа коэффициентов в уравнении: введите столько коэффициентов, сколько провели независимых опытов, и получите остаточную сумму, равную нулю. Поэтому предпочитают относить ее на один «свободный» опыт. Число таких опытов называется числом степеней свободы (f).

Для проверки гипотезы об адекватности можно использовать F–критерий или критерий Фишера.

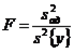(3)

где s²_ад – дисперсия адекватности, s²_{y} – дисперсия воспроизводимости (1), F – критерий Фишера.

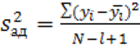, где l – число значимых коэффициентов.

Проверку гипотезы об адекватности модели сведем к сравнению с табличным значением (прил. 2).

Полученное значение критерия Фишера сравнивают с табличным значением.

Если F_т < F_р, то уравнение регрессии адекватно (тождественно) описывает процесс.

Квантили (значения критерия Фишера) определяют уровнем значимости (степенью ошибки 0,05), числом степеней свободы и числом значимых коэффициентов.

Задание

Данные вычислительного эксперимента для обработки

№ опыта	Кодированные параметры	y1	y2	y3
х0	х1	х2	х3	х1х2	х2х3	х1х3
1.	+	+	+	+	+	+	+	0.2	0.22	0.2
2.	+	+	+	-	+	-	-	0.1	0.11	0.08
3.	+	+	-	+	-	-	+	0.14	0.14	0.17
4.	+	+	-	-	-	+	-	0.11	0.1	0.13
5.	+	-	+	+	-	+	-	0.26	0.23	0.29
6.	+	-	+	-	-	-	+	0.13	0.1	0.12
7.	+	-	-	+	+	-	-	0.19	0.2	0.3
8.	+	-	-	-	+	+	+	0.09	0.11	0.09

1.Рассчитать дисперсию (воспроизводимости) 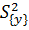(1)

2.Оценить однородность дисперсий методом Кохрена (см. лаб. № 4_2)

3.Рассчитать коэффициенты уравнения регрессии по формулам

,

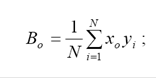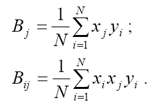
4. Составить математическую модель.

5. Рассчитать доверительный интервал коэффициентов уравнений регрессии (2) и оценить значимость коэффициентов.

6. Проверить полученную модель на адекватность (3).

Приложение № 1

Таблица 1

Критические значения коэффициента Стьюдента (t-критерия) для различной доверительной вероятности p и числа степеней свободы f

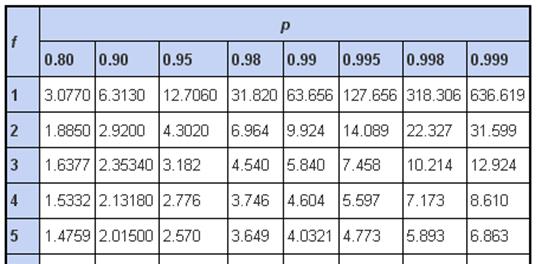
Приложение № 2

Таблица 2

Квантили распределения Фишера F для p = 0,05

Степени свободы f1 (ад)	Степени свободы f2 (дисп. воспр)
								∞
	164,4	199,5	215,7	224,6	230,2	234,0	244,9	249,0	254,3
	18,5	19,2	19,2	19,3	19,3	19,3	19,4	19,5	19,5
	10,1	9,6	9,3	9,1	9,0	8,9	8,7	8,6	8,5
	7,7	6,9	6,6	6,4	6,3	6,2	5,9	5,8	5,6
	6,6	5,8	5,4	5,2	5,1	5,0	4,7	4,5	4,4
	6,0	5,1	4,8	4,5	4,4	4,3	4,0	3,8	3,7
	5,6	4,7	4,4	4,1	4,0	3,9	3,6	3,4	3,2

1.

№ опыта	Кодированные параметры	y1	y2	y3	s2
х0	х1	х2	х3	х1х2	х2х3	х1х3
1.	+	+	+	+	+	+	+	0.2	0.22	0.2	0,000132
2.	+	+	+	-	+	-	-	0.1	0.11	0.08	0,003847
3.	+	+	-	+	-	-	+	0.14	0.14	0.17	0,0003
4.	+	+	-	-	-	+	-	0.11	0.1	0.13	0,0002335
5.	+	-	+	+	-	+	-	0.26	0.23	0.29	0,0009
6.	+	-	+	-	-	-	+	0.13	0.1	0.12	0,0002335
7.	+	-	-	+	+	-	-	0.19	0.2	0.3	0,0037
8.	+	-	-	-	+	+	+	0.09	0.11	0.09	0,0001335

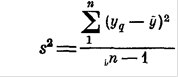
2.

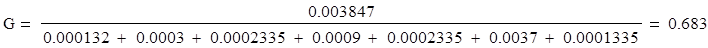
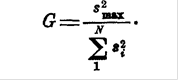
G_табл.=0.4377

Экспериментальное значение больше табличного значения, следовательно, дисперсии нельзя считать однородными.

3.

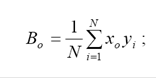
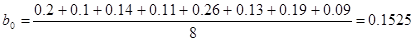
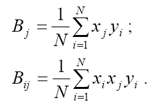
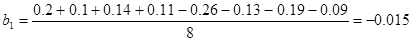
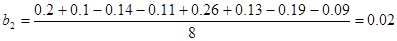
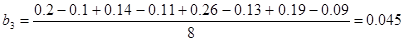
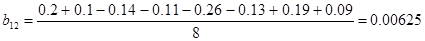
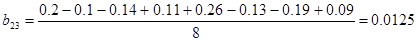
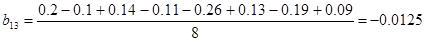
4.Математическая модель

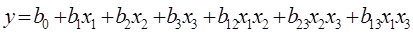
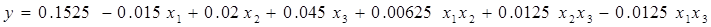
5.

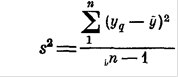
Для y1 s²=0.0035

Дисперсию коэффициента регрессии

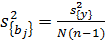
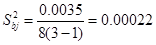
Доверительный интервал

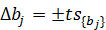
t – табличное значение критерия в выбранном уровне значимости 0,05

t=4,3020

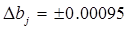
Все коэффициенты уравнения регрессии значимы, так как они все больше доверительного интервала. Наибольшее влияние оказывает параметр x3.

6.

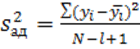
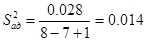
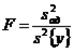
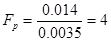
F_табл=3.9

Так как F_р>F_табл ,то можно сделать вывод, что уравнение регрессии адекватно (тождественно) описывает процесс.