Методом крутильных колебаний
Цель работы: определение момента инерции тела методом крутильных колебаний.
Приборы и принадлежности: крутильный маятник с миллисекундомером, стальной цилиндр, стальной прямоугольный параллелепипед и штангенциркуль.
Теоретические сведения
Твердое тело можно рассматривать как систему материальных точек, расстояния между которыми остаются постоянными. Вращательным движением твердого тела называют такое перемещение, при котором все точки тела описывают окружности вокруг общей оси вращения.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
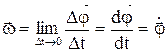 . (5.1)
. (5.1)
Размерность угловой скорости 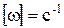 , а ее единица измерения - радиан в секунду (рад/с).
, а ее единица измерения - радиан в секунду (рад/с).
Направление вектора угловой скорости совпадает с направлением перемещения острия правого винта, головка которого вращается по часовой стрелке в направлении движения точки по окружности, т.е. по правилу правого винта.
Модуль линейной скорости точки, движущейся равномерно по окружности радиуса R,
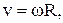 (5.2)
(5.2)
где 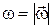
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
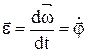 . (5.3)
. (5.3)
Из этой формулы следует, что вектор углового ускорения направлен по оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 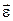 параллелен вектору
параллелен вектору 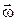 , при замедленном - антипараллелен.
, при замедленном - антипараллелен.
Тангенциальная составляющая ускорения
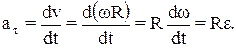 (5.4)
(5.4)
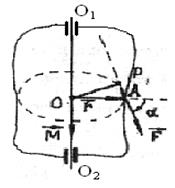 Рис. 5.1 Рис. 5.1 | Нормальная составляющая ускорения 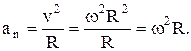 (5.5) Рассмотрим твердое тело, закрепленное на неподвижной оси (5.5) Рассмотрим твердое тело, закрепленное на неподвижной оси 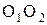 (рис.5.1). Пусть в точке А приложена сила (рис.5.1). Пусть в точке А приложена сила 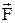 , причем вектор этой силы лежит в плоскости, перпендикулярной оси вращения , причем вектор этой силы лежит в плоскости, перпендикулярной оси вращения 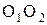 . . |
В точке О пересекаются эта плоскость и ось 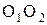 .Радиус-вектор
.Радиус-вектор 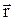 указывает положение точки А относительно точки О,
указывает положение точки А относительно точки О, 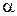 - угол между вектором
- угол между вектором 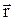 и вектором
и вектором 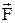 . Опустим перпендикуляр ОР на прямую, вдоль которой действует сила
. Опустим перпендикуляр ОР на прямую, вдоль которой действует сила 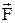 . Длина отрезка ОР
. Длина отрезка ОР 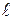
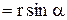 , где
, где 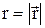 . Это кратчайшее расстояние между линией действия силы и осью вращения называется плечом силы.
. Это кратчайшее расстояние между линией действия силы и осью вращения называется плечом силы.
Момент силы - величина векторная, равная векторному произведению 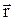 и
и 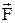 :
:
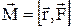 .
.
Направление вектора 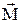 определяется следующим образом: вектор
определяется следующим образом: вектор 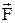 переносят параллельно самому себе так, чтобы его начало совпало с точкой О. Через векторы
переносят параллельно самому себе так, чтобы его начало совпало с точкой О. Через векторы 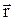 и
и 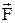 проводят плоскость и восстанавливают перпендикуляр к ней в точке О. Мысленно вращают вектор
проводят плоскость и восстанавливают перпендикуляр к ней в точке О. Мысленно вращают вектор 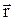 по часовой стрелке по кратчайшему пути до совмещения с вектором
по часовой стрелке по кратчайшему пути до совмещения с вектором 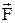 . Направление перемещения острия правого винта указывает направление вектора
. Направление перемещения острия правого винта указывает направление вектора 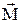 , лежащего на перпендикуляре (на рис. 5.1 вектор
, лежащего на перпендикуляре (на рис. 5.1 вектор 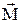 лежит на оси вращения
лежит на оси вращения 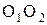 и направлен вниз).
и направлен вниз).
Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс материальных точек системы на квадрат их расстояний до рассматриваемой оси:
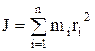 , (5.6)
, (5.6)
где 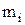 - масса i-й точки, находящейся на расстоянии
- масса i-й точки, находящейся на расстоянии 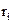 от оси вращения.
от оси вращения.
В случае непрерывного распределения масс эта сумма сводится к интегралу по объему тела V:
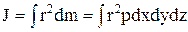 ,
,
где р=р(х,у,z) - плотность тела в данной точке.
Если тело и плотность его постоянная величина по всему объему,
то при 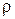 =const
=const
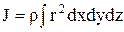
Пусть сила 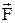 приложена к телу, закрепленному на неподвижной оси (рис. 5.1). Эта сила создает момент
приложена к телу, закрепленному на неподвижной оси (рис. 5.1). Эта сила создает момент 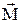 , и под действием этого момента тело приобретает угловое ускорение
, и под действием этого момента тело приобретает угловое ускорение 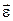 . Угловое ускорение пропорционально моменту силы, приложенной к телу:
. Угловое ускорение пропорционально моменту силы, приложенной к телу:
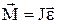 , (5.7)
, (5.7)
где J - момент инерции тела относительно оси вращения. Это уравнение представляет собой основное уравнение динамики вращательного движения твердого тела.
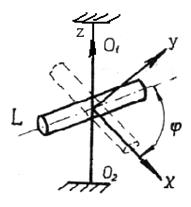 Рис. 5.2 Рис. 5.2 | На рис. 5.2 показан крутильный маятник. На металлической проволоке закреплен стержень L так, что вертикальная ось  проходит через центр массы стержня. Введем неподвижную прямоугольную систему координат (х,у,z), причем ось z совпадает с осью проходит через центр массы стержня. Введем неподвижную прямоугольную систему координат (х,у,z), причем ось z совпадает с осью  . . |
При отклонении стержня на угол  от оси x в плоскости, перпендикулярной оси z, стержень будет совершать крутильные колебания вокруг оси
от оси x в плоскости, перпендикулярной оси z, стержень будет совершать крутильные колебания вокруг оси 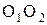 .
.
Для описания движения стержня используем основное уравнение динамики вращательного движения:
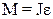
где 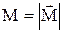 - модуль момента сил, действующих на стержень со стороны проволоки; J - момент инерции стержня относительно оси
- модуль момента сил, действующих на стержень со стороны проволоки; J - момент инерции стержня относительно оси 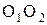
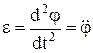 - угловое ускорение.
- угловое ускорение.
В то же время момент сил М будет пропорционален углу отклонения 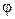 при
при
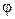 ≤
≤ 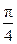 ;
;
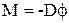 , (5.8)
, (5.8)
где D - модуль кручения проволоки. Знак минус в этой формуле указывает, что вектор момента 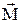 направлен в противоположную сторону вектору угла
направлен в противоположную сторону вектору угла 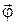 .
.
Таким образом, можно записать, пренебрегая силами трения:
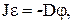
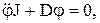
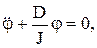
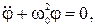
где 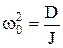 . (5.9)
. (5.9)
Решение уравнение (5.9) имеет вид
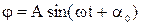 . (5.10)
. (5.10)
В этой формуле А - амплитуда колебаний; 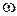 - циклическая частота
- циклическая частота 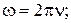
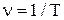 ;
; 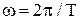 ,
,
где ν - частота колебаний (линейная частота), Т - период колебаний; t -время; 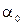 - начальная фаза. Величина
- начальная фаза. Величина 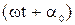 называется фазой колебаний.
называется фазой колебаний.
Подставив выражение (5.10) в (5.9), получаем
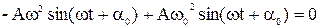
Это равенство выполняется при
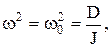
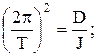
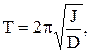 (5.11)
(5.11)
где Т - период собственных колебаний крутильного маятника.
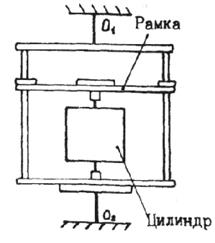
Рис. 5.3
Закрепим в рамке крутильного маятника (рис. 5.3) металлический цилиндр. Пусть Jl - момент инерции рамки без цилиндра, J2 - момент инерции цилиндра относительно оси симметрии, совпадающей с осью вращения 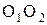 . Период свободных крутильных колебаний рамки без
. Период свободных крутильных колебаний рамки без
цилиндра
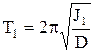 . (5.12)
. (5.12)
Если в рамке закреплен цилиндр, то момент инерции этой системы относительно оси вращения 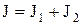 и, соответственно, период свободных крутильных колебаний системы
и, соответственно, период свободных крутильных колебаний системы
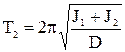 . (5.13)
. (5.13)
Момент инерции цилиндра относительно его оси симметрии, проходящей перпендикулярно основанию,
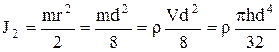 , (5.14)
, (5.14)
где m - масса; r - радиус; h - высота; d – 2r - диаметр; 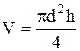 - объем;
- объем; 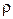 - плотность материала цилиндра.
- плотность материала цилиндра.
Если измерены периоды свободных крутильных колебаний T1 и Т2, то из выражений (5.12) и (5.13) следует, что
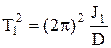 , (5.15)
, (5.15)
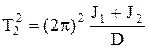 . (5.16)
. (5.16)
Из (5.15) находим модуль кручения проволоки
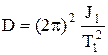 .
.
Подставим это выражение D в (5.16)
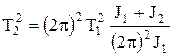 .
.
Отсюда
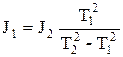 . (5.17)
. (5.17)
Выражение (5.17) подставляем в уравнение (5.15) и находим
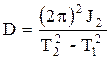 . (5.18)
. (5.18)
Закрепим в рамке прямоугольный металлический параллелепипед так, чтобы одна из его осей симметрии z, называемая главной осью, совпала с осью вращения рамки 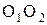 (рис. 5.4).
(рис. 5.4).
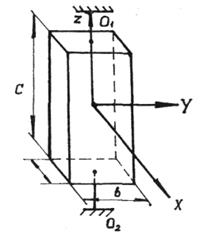 Рис. 5.4 Рис. 5.4 | Момент инерции этой системы 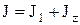 , где , где 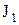 - момент инерции рамки относительно оси вращения - момент инерции рамки относительно оси вращения 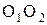 ; ; 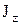 -момент инерции прямоугольного параллелепипеда относительно главной оси z. Период свободных крутильных колебаний согласно формуле (5.13) -момент инерции прямоугольного параллелепипеда относительно главной оси z. Период свободных крутильных колебаний согласно формуле (5.13) 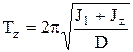 (5.19) (5.19) |
Отсюда
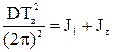 (5.20)
(5.20)
Подставим в (5.20) выражения (5.17) и (5.18):
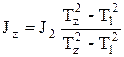 (5.21)
(5.21)
Затем в (5.21) подставим (5.14):
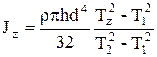 , (5.22)
, (5.22)
где Jz - момент инерции прямоугольного параллелепипеда относительно главной оси симметрии z; 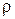 - плотность материала цилиндра; h и d -высота и диаметр цилиндра; Т1 - период свободных крутильных колебаний рамки без груза; Тz - период свободных крутильных колебаний рамки с прямоугольным параллелепипедом относительно главной оси z; Т2 - период свободных крутильных колебаний рамки с цилиндром.
- плотность материала цилиндра; h и d -высота и диаметр цилиндра; Т1 - период свободных крутильных колебаний рамки без груза; Тz - период свободных крутильных колебаний рамки с прямоугольным параллелепипедом относительно главной оси z; Т2 - период свободных крутильных колебаний рамки с цилиндром.
Моменты инерции прямоугольного параллелепипеда относительно главных осей х и у, соответственно, равны
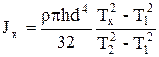 , (5.23)
, (5.23)
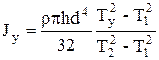 . (5.24)
. (5.24)
Здесь Тх и Тy - периоды свободных крутильных колебаний рамки с прямоугольным параллелепипедом относительно главных осей х и у.
Теоретические вычисления дают при 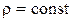
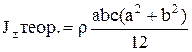 , (5.25)
, (5.25)
где а, b, с - размеры параллелепипеда, соответственно вдоль осей х, y, z.
Моменты инерции относительно главных осей х и у находятся по формулам
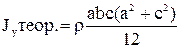 , (5.26)
, (5.26)
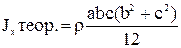 . (5.27)
. (5.27)
На основании формулы (5.22) находим границу общей погрешности измерения момента инерции параллелепипеда относительно оси z.
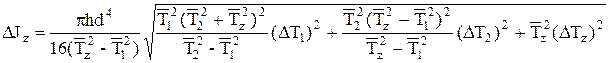 . (5.28)
. (5.28)
Чтобы найти выражения для 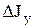 или
или 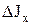 , нужно индекс «z» в формуле (5.28) заменить, соответственно, на «у» или «х».
, нужно индекс «z» в формуле (5.28) заменить, соответственно, на «у» или «х».
В формуле (5.28) не учитываются погрешности измерения высоты h и диаметра d цилиндра. Значения величин 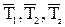 и ∆Т1, ∆Т2, ∆Тz вычисляются по формулам
и ∆Т1, ∆Т2, ∆Тz вычисляются по формулам
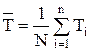 (5.29)
(5.29)
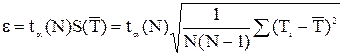 , (5.30)
, (5.30)
где 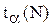 - коэффициент Стьюдента; N - количество измерений;
- коэффициент Стьюдента; N - количество измерений;
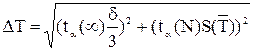 , (5.31)
, (5.31)
где 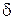 =0,0005c – предел допустимой погрешности измерений времени.
=0,0005c – предел допустимой погрешности измерений времени.
Описание установки
Прибор “Крутильный маятник” представлен на рис.5.5. На основании (1), оснащенном четырьмя ножками с регулируемой высотой, находится миллисекундомер (2).
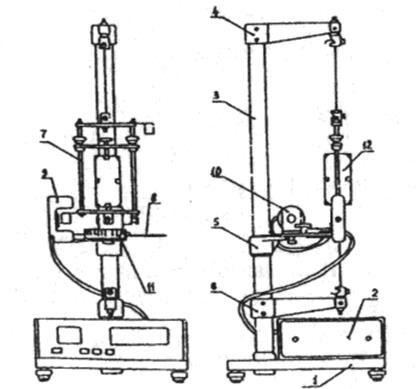
Рис. 5.5
В основании установлена колонка (3), на которой при помощи прижимных винтов закреплены кронштейны (4, 5 и 6). Кронштейны (4) и (6) имеют зажимы, служащие для фиксации стальной проволоки, на которой подвешена рамка (7). На кронштейне (5) находится стальная плита (8), которая служит основанием фотоэлектрического датчика (9), электромагнита (10) и угольной шкалы (11). Электромагнит (10) может изменять положение на плите, а его положение относительно фотоэлектрического датчика показывает на угольной шкале стрелка, прикрепленная к электромагниту.
Конструкция рамки позволяет закреплять грузы (12), значительно отличающиеся друг от друга по внешним размерам. Грузы крепятся при помощи подвижной балки, которая перемещается по направляющим между неподвижными балками, она фиксируется путем затягивания гаек на зажимных втулках, помещенных на подвижной балке.
Фотоэлектрический датчик и электромагнит соединены с миллисекундомером при помощи разъема.
На лицевой панели миллисекундомера размещены следующие элементы: «сеть» - выключатель сети. Нажатие этой клавиши включает питающее напряжение; «сброс» - сброс показаний миллисекундомера; пуск -нажатие этой клавиши выключает электромагнит и освобождает рамку (7); «стоп» - окончание измерения.
Порядок выполнения работы
Задание I. Определение периода колебаний крутильного маятника.
1. Включить сетевой шнур в питающую сеть.
2. Нажать на клавишу «сеть».
3. Установить электромагнит в заданном положении на плите так, чтобы
стрелка указывала на угол 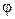 <45°. Зафиксировать электромагнит с по
<45°. Зафиксировать электромагнит с по
мощью гайки.
4. В рамке прибора закрепить исследуемый груз.
5. Поворачивая рамку прибора, приблизить ее стрелку к электромагниту таким образом, чтобы магнитная сила фиксировала положение рамки.
6. Нажать клавишу «пуск».
7. После подсчета измерителем 9 периодов крутильных колебаний нажать клавишу «стоп». При этом маятник совершит еще одно колебание
и период одного полного колебания определяется по формуле Т=t/n, где
t - время колебаний; n - количество колебаний (n=10).
Задание II. Определение моментов инерции прямоугольного
параллелепипеда относительно главных осей.
1. Измерить с помощью штангенциркуля диаметр dи высоту h стального цилиндра с точностью до ±0,2мм. Измерить длины ребер стального параллелепипеда а, b, с с точностью до 0,2мм. Причем размеры ребер выбираются таким образом, чтобы a≤b≤c. Записать данные:
Число измерений N=5; 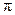 (РI)=3,1415
(РI)=3,1415
Плотность 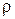 (R)=7,8 г/см3
(R)=7,8 г/см3
Диаметр d(D) = см
Высота h(Н) = см
Коэффициент Стьюдента (ТАВ) tα(∞)=
Коэффициент Стьюдента (TANEND) tα(5)=
Длина по оси х (А) а = см
Длина по оси у (В) в = см
Длина по оси z(С) с = см
2. Измерить период 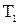 свободных крутильных колебаний рамки без груза. Измерения провести 5 раз (N=5).
свободных крутильных колебаний рамки без груза. Измерения провести 5 раз (N=5).
3. Установить в рамке стальной цилиндр и измерить 5 раз период 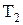 свободных колебаний рамки с цилиндром.
свободных колебаний рамки с цилиндром.
4. Установить в рамке стальной прямоугольный параллелепипед так,
чтобы наибольшее по длине ребро c было параллельно оси вращения 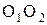 . Измерить 5 раз период
. Измерить 5 раз период 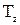 свободных крутильных колебаний рамки с этим грузом.
свободных крутильных колебаний рамки с этим грузом.
5. Заполнить таблицу результатов измерений.
Таблица
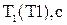 | 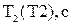 | 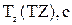 | 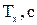 | 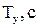 |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
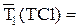 | 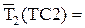 | 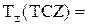 | 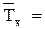 | 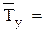 |
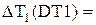 | 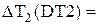 | 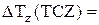 | ∆Тx = | ∆Ту = |
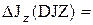 | 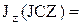 |
6. Выбрать доверительную вероятность α и найти коэффициенты Стьюдента 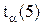 и
и 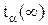
7. По формуле (5.29) вычислить средние значения 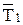
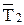 и
и 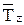
8. По формуле (5.30) вычислить доверительные границы ε случайных погрешностей измерений периодов колебаний Т1 Т2 и Тz.
9. По формуле (5.31) вычислить доверительные границы ΔТ общих погрешностей измерений периодов колебаний Т1 Т2 и Тz.
10. По формуле (5.28) вычислить доверительную границу общей погрешности измерения момента инерции ∆JZ.
11. По формуле (5.22) найти среднее значение 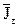 , подставив в нее средние значения
, подставив в нее средние значения 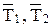 и
и 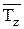 .
.
12. Записать экспериментально найденное значение момента инерции прямоугольного параллелепипеда относительно главной оси z в виде
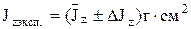 ,
,
при α =
13. По формуле (5.25) вычислить теоретическое значение момента инерции 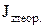 сравнить с экспериментальным значением
сравнить с экспериментальным значением 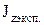
14. Для измерения момента инерции прямоугольного параллелепипеда
относительно главной оси х параллелепипед закрепить в рамке так,
чтобы его ребро длиной а было параллельно оси вращения рамки 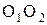 .
.
Затем нужно измерить 5 раз период Тх свободных крутильных колебаний рамки с параллелепипедом. Далее во всех расчетных формах необходимо заменить Tz на Тх и вычислить значения  . При этом используются уже найденные значения
. При этом используются уже найденные значения 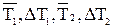 . Результат измерений записать в виде
. Результат измерений записать в виде
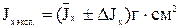
при α =
15. Вычислить по формуле (5.27) теоретическое значение момента инерции Jx теор и сравнить Jx эксп.
16. Измерения момента инерции прямоугольного параллелепипеда относительно главной оси у провести аналогично: параллелепипед закрепить в рамке так, чтобы его ребро длиной было параллельно оси вращения рамки 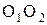 . Измерить 5 раз период Ту свободных крутильных колебаний рамки с параллелепипедом. Во всех расчетных формах заменить Tz на Ту и вычислить значения
. Измерить 5 раз период Ту свободных крутильных колебаний рамки с параллелепипедом. Во всех расчетных формах заменить Tz на Ту и вычислить значения 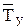 ,
, 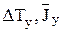 и
и 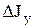 . Результат измерений записать в виде
. Результат измерений записать в виде
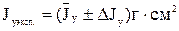
при α =
17. Вычислить по формуле (5.26) теоретическое значение момента инерции Jy теор. и сравнить с Jy эксп .
Для расчета на компьютере величин 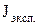 и
и 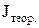 можно пользоваться программой "Маятник". Для этого в память машины нужно ввести исходные данные, записанные в п. 1 (в скобках указаны обозначения величин, используемых для ввода данных в память компьютера).
можно пользоваться программой "Маятник". Для этого в память машины нужно ввести исходные данные, записанные в п. 1 (в скобках указаны обозначения величин, используемых для ввода данных в память компьютера).
Контрольные вопросы
1. Какое движение твердого тела называется вращательным? Дать определение угловой скорости и углового ускорения. Как направлены
векторы угловой скорости и углового ускорения?
2. Как связана линейная скорость точки, движущейся по окружности с угловой скоростью? Что собой представляют тангенциальная и нормальная составляющие ускорения? Их связь с угловой скоростью и угловым ускорением.
3. Что такое момент инерции системы материальных точек относительно
оси вращения? Дать определение момента инерции при непрерывном
распределении масс.
4. Что называется моментом силы относительно некоторой точки О? Дать определение момента силы в векторной форме.
5. Вывести основное уравнение динамики вращательного движения твердого тела.
6. Вывести дифференциальное уравнение, описывающее движение крутильного маятника. Записать решение этого уравнения. Какие колебания называются свободными?
7. Что такое гармонические колебания? Что называется периодом колебаний? Дать определение амплитуды, циклической частоты, фазы и начальной фазы гармонических колебаний.
ЛАБОРАТОРНАЯ РАБОТА №6
